4 Sobreajuste y subajuste

Una vez que hemos establecido el propósito de los modelos predictivos, y algunos métodos básicos, quisiéramos contestar: ¿De qué depende el desempeño de un modelo predictivo? ¿Cómo podemos mejorarlo?

Supongamos primero, teóricamente, que conocemos toda la población de interés para la que queremos hacer predicciones. Supondremos que nuestra medida de error es el error cuadrático. Al menos en teoría, si conocemos toda la población, entonces existe predictor óptimo \(f^{*}\) tal que para cualquier \(x\) que observemos y cualquier otro predictor \(f\), tenemos que \[Err^* = E((y - f^{*}(x))^2) \leq E((y - f(x))^2)\] En este caso de pérdida cuadrática, la solución es simplemente \[f^{*}(x) = E(y|x)\] Y este predictor es el que da menor error cuadrático medio. El error irreducible lo definimos como la diferencia

\[\epsilon = y - f^{*}(x)\]

Estos errores provienen de que \(x\) no contiene toda la información necesaria para determinar el valor \(y\) de manera única.

En la práctica, sin embargo, nosotros sólo tenemos una muestra para entrenar nuestros modelos:

\[{\mathcal L} = (x^{(1)}, y^{(1)}), (x^{(2)}, y^{(2)}), \ldots, (x^{(N)}, y^{(N)}) \] Y ajustamos un modelo \(\hat{f} = f_{\mathcal L}\), usando estos datos. Nuestra predicción para las entradas \(x\) es \(\hat{y} = \hat{f}(x)\). Podemos escribir

\[y - \hat{f}(x) = (f^*(x) - \hat{f}(x)) + \epsilon,\] de modo que el valor verdadero \(y\) puede estar lejos de \(\hat{f}(x)\) cuando:

1. La perturbación que depende de otras variables no medidas \(\epsilon\) es grande (error irreducible)
2. Nuestra función de predicción \(\hat{f}\) está lejos de la \(f\) del proceso generador de datos.

En cuanto al primer problema, podemos hacer más chico el error irreducible creando distintas variables derivadas a partir de las que tenemos, o buscando más información relevante para incluir en \(x\) que nos ayude a predecir \(y\). La segunda razón es la que nos interesa más por el momento.

Veamos un ejemplo con datos simulados

library(tidyverse)
library(patchwork)
set.seed(1424)
simular_ejemplo <- function(n, sd = 500){
  x <- runif(n, 0, 20)
  y <- ifelse(x < 10, 1000*sqrt(x), 1000*sqrt(10))
  y <- y + rnorm(n, 0, sd = sd)
  tibble(id = 1:n, x = x, y = y)
}
datos_entrena <- simular_ejemplo(60)
datos_f <- tibble(x = seq(0, 20, 0.1)) |> 
  mutate(f = ifelse(x < 10, 1000*sqrt(x), 1000*sqrt(10)))
g_datos <- ggplot(datos_entrena, aes(x = x, y = y)) + 
  geom_point() + 
  labs(subtitle = "Lo que vemos")
g_verdadera <-  ggplot(datos_f, aes(x = x)) + 
  geom_point(data = datos_entrena, aes(y = y)) +
  geom_line(aes(y = f), colour = "#56B4E9", size = 2) +
  labs(subtitle = "Predictor óptimo")
g_ajuste <- ggplot(datos_entrena, aes(x = x, y = y)) + 
  geom_point(data = datos_entrena) +
  geom_smooth(method = "loess", colour = "red", span = 0.5, size = 2, se= FALSE) +
  labs(subtitle = "Lo que estimamos")
g_datos + g_verdadera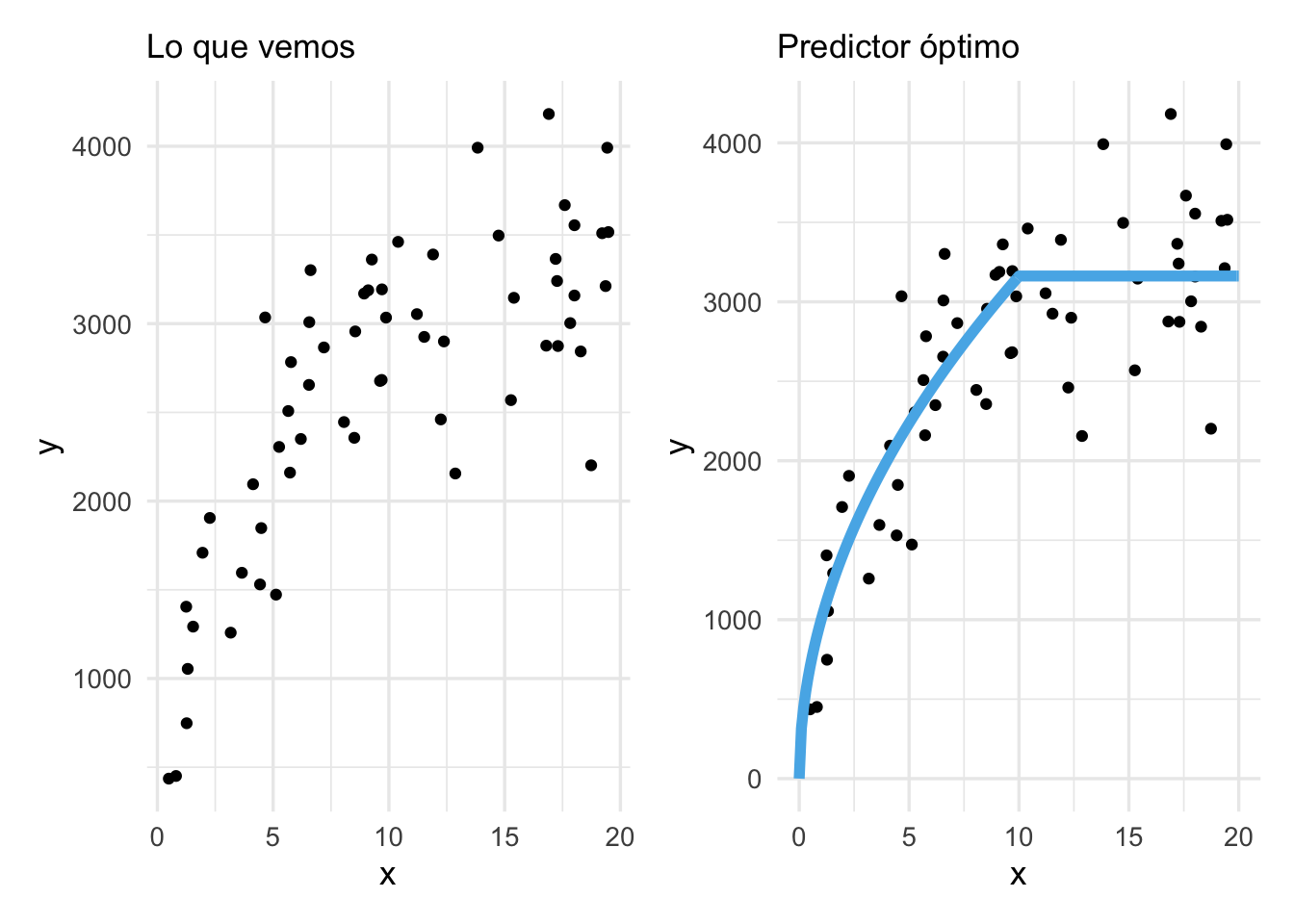 

Para problemas reales no conocemos la forma de la función \(f^*\) marcada en azul, sino que tenemos que inferirla de los puntos que observamos.

4.1 ¿Por qué \(\hat{f}\) está lejos de \(f^*\)?

Hay dos razones por las que nuestra estimación \(\hat{f}(x)\) puede estar lejos de \(f^*(x)\), donde supondremos por ahora que \(x\) está fija.

1. (Sesgo) Esta diferencia es sistemáticamente grande para cualquier muestra de entrenamiento \(\mathcal L\) que obtengamos, y \(\hat{f}(x)\) no cambia mucho cuando cambia la muestra de entrenamiento.
2. (Variabilidad) \(\hat{f}\) es muy variable, de modo que típicamente, para una muestra particular que observemos, \(\hat{f}(x)\) cae lejos de \(f^*(x)\).

Y una tercera posibilidad es que tanto 1 como 2 ocurran. Podemos ver esto en el ejemplo simulado que vimos anteriormente:

4.2 Ejemplo: ajuste lineal

Primero veamos qué sucede con regresión lineal y distintas muestras de entrenamiento:

library(tidymodels)
mis_metricas <- metric_set(mae)
receta_simple <- recipe(y ~ ., data = datos_entrena) |>
  update_role(id, new_role = "id")
modelo <- linear_reg() |> set_engine("lm")

flujo_simple <- workflow() |> 
  add_recipe(receta_simple) |> 
  add_model(modelo)

Usaremos 100 muestras de entrenamiento:

reps <- 1:100
graf_lm_tbl <- map_df(reps, function(rep){
  datos_entrena <- simular_ejemplo(15)
  ajuste <- fit(flujo_simple, datos_entrena)
  datos_x <- tibble(x = seq(0, 20, 0.1), id = NA)
  preds <- predict(ajuste, datos_x) |> 
    bind_cols(datos_x) |> 
    mutate(rep = rep) |>
    group_by(rep) |> nest()
  datos_entrena <- datos_entrena |> mutate(rep = rep) |> 
    group_by(rep) |> nest()
  left_join(datos_entrena, preds, by = "rep", suffix = c("_entrena", "_ajuste"))
})

Y graficamos las primeras 9:

ggplot(graf_lm_tbl |> unnest(cols = data_ajuste) |> filter(rep < 10)) +
  geom_line(aes(x =x, y = .pred, group = rep), colour = "#E69F00", size = 1.2) + 
  geom_point(data = graf_lm_tbl |> unnest(cols = data_entrena) |> filter(rep < 10), 
             aes(x = x, y = y)) +
  geom_line(data = datos_f, aes(x = x, y =f), colour = "#56B4E9", size=1.2) +
  facet_wrap(~rep)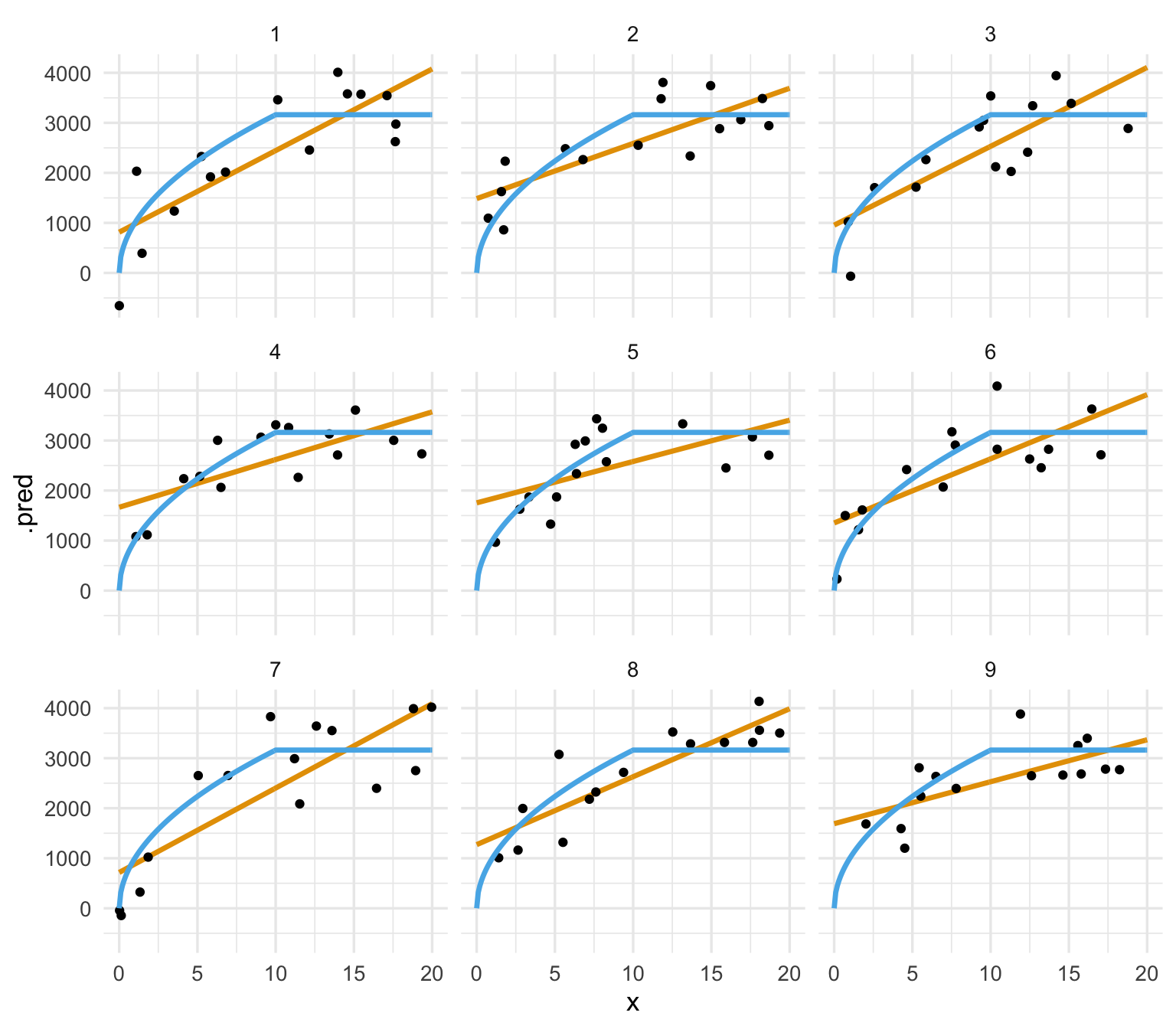

Observaciones:

1. El ajuste no varía mucho de muestra a muestra de entrenamiento. Quiere decir que el error de predicción del modelo lineal no se debe tanto a variabilidad.
2. Sin embargo, vemos errores sistemáticos en las predicciones. Por ejemplo, alrededor de 10, la mayoría de las observaciones (negro) están por encima de la predicción (línea roja). Cerca de 0, las predicciones del modelo lineal son tienden a ser demasiado altas.
3. Concluimos que una buena parte del error del modelo lineal es debido a sesgo: esta estructura lineal no es apropiada para los datos, y tendemos a sobre o subpredecir en distintas partes de manera consistente.

4.3 Ejemplo: vecinos más cercanos

En contraste, veamos qué pasa con un método local:

modelo <- nearest_neighbor(n = 1) |> 
  set_mode("regression") |> set_engine("kknn")
flujo_simple <- workflow() |> 
  add_recipe(receta_simple) |> 
  add_model(modelo)

Usaremos 100 muestras de entrenamiento:

reps <- 1:100
graf_vmc_tbl <- map_df(reps, function(rep){
  datos_entrena <- simular_ejemplo(15)
  ajuste <- fit(flujo_simple, datos_entrena)
  datos_x <- tibble(x = seq(0, 20, 0.5), id = NA)
  preds <- predict(ajuste, datos_x) |> 
    bind_cols(datos_x) |> 
    mutate(rep = rep) |>
    group_by(rep) |> nest()
  datos_entrena <- datos_entrena |> mutate(rep = rep) |> 
    group_by(rep) |> nest()
  left_join(datos_entrena, preds, by = "rep", suffix = c("_entrena", "_ajuste"))
})

Y graficamos las primeras 20:

ggplot(graf_vmc_tbl |> unnest(cols = data_ajuste) |> filter(rep < 10)) +
  geom_line(aes(x =x, y = .pred, group = rep), colour = "#E69F00", size = 1.2) + 
  geom_point(data = graf_vmc_tbl |> unnest(cols = data_entrena) |> filter(rep < 10), 
             aes(x = x, y = y)) +
  geom_line(data = datos_f, aes(x = x, y =f), colour = "#56B4E9", size=1.2) +
  facet_wrap(~rep)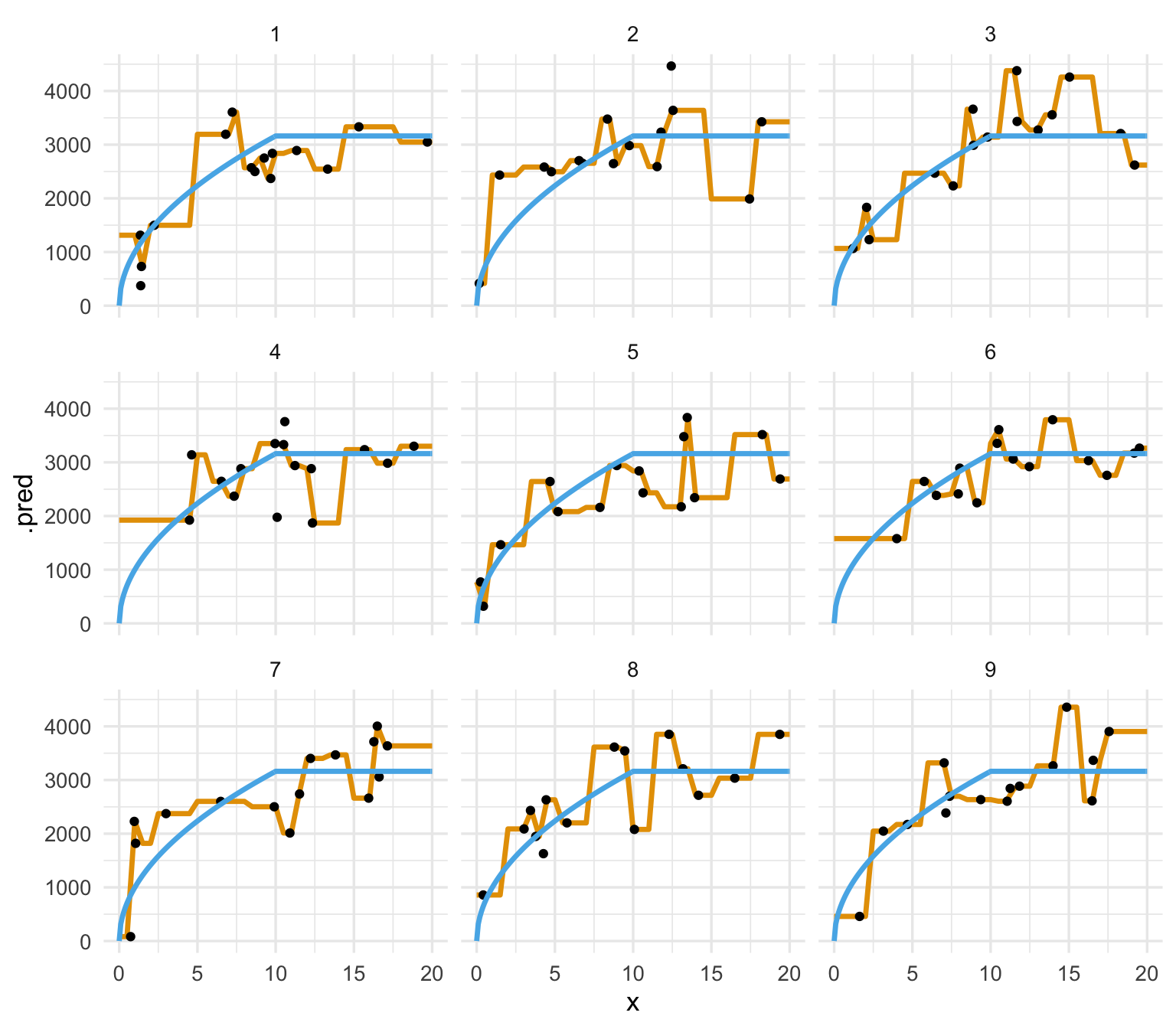

Observaciones:

1. El ajuste varía considerablemente de muestra a muestra de entrenamiento. Esto quiere decir que una buena parte del error de predicción se debe a variabilidad.
2. No vemos errores sistemáticos en las predicciones.
3. Concluimos que la mayor parte del error de este modelo de 2 vecinos más cercanos es debido a variabilidad: los datos de entrenamiento mueven mucho a las predicciones.

Finalmente, podemos ver lo que sucede alrededor de \(x = 10\) por ejemplo, extrayendo predicciones:

preds_lm <- graf_lm_tbl |> unnest(cols = data_ajuste) |> 
  ungroup() |> filter(x == 10) |> mutate(tipo = "lineal")
preds_vmc <- graf_vmc_tbl |> unnest(cols = data_ajuste) |> 
  ungroup() |> filter(x == 10) |> mutate(tipo = "1-vmc")
preds_2 <- bind_rows(preds_lm, preds_vmc)

ggplot(datos_f |> filter(x > 5, x < 15)) +
  geom_line(aes(x = x, y = f), colour = "#56B4E9", size = 2) +
  geom_boxplot(data = preds_2, aes(x = x, y = .pred, colour = tipo))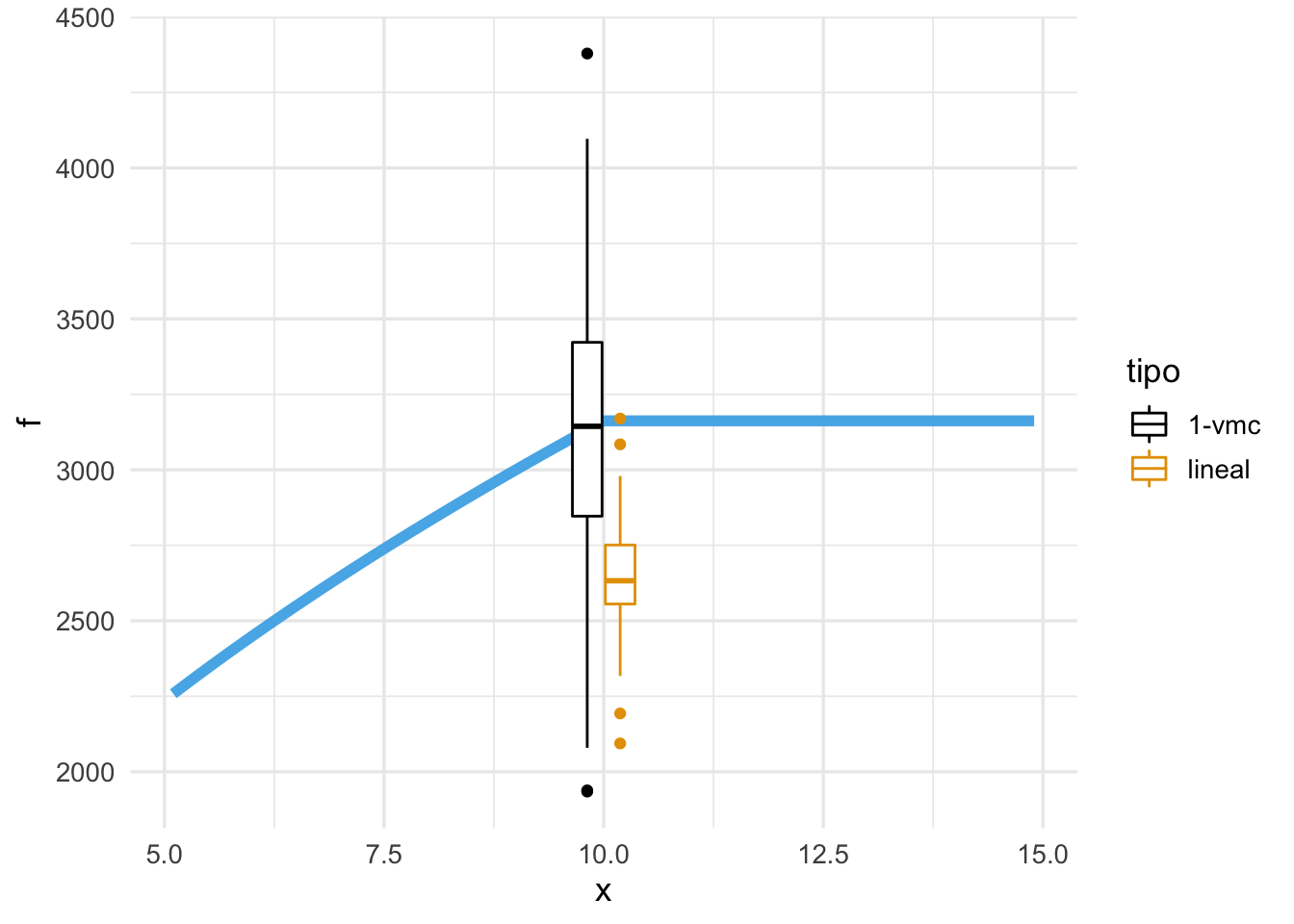 

Estos dos modelos fallan en \(x = 10\) por razones muy diferentes: uno tiene una estructura rígida que sesga las predicciones y el otro es demasiado flexible, lo que produce alta variabilidad con cambios chicos en la muestra de entrenamiento.

El desempeño de un modelo predictivo puede ser malo por dos razones, que pueden ocurrir simultáneamente:

• La forma del modelo es demasiado flexible, lo cual lo hace fuertemente dependiente de los datos de entrenamiento. El riesgo es que esta dependencia lo sujeta a particularidades de la muestra particular de entrenamiento que estamos usando, o dicho de otra manera “el modelo aprende ruido”. Las predicciones son inestables o variables.
• La forma del modelo es demasiado rígido, lo cual hace difícil adaptarlo a patrones que existen en los datos de entrenamiento. El riesgo es que esta falta de adaptabilidad no permite que “el modelo aprenda de los datos” patrones útiles para predecir. Las predicciones son consistentemente malas.

Muchas veces decimos que modelos que sufren principalmente de varianza están sobreajustados, y que aquellos que sufren principalmente de sesgo tienen subajuste.

En el caso del error cuadrático medio, es posible demostrar que, en un punto fijo x, se cumple la descomposición sesgo-varianza:

\[\hat{Err}(x) = (E(\hat{f}(x)) - f^*(x))^2 + Var(\hat{f}(x)) + \sigma_x^2,\]

donde el valor esperado y la varianza son cantidades teóricas que se calculan sobre las posibles muestras de entrenamiento. El primer término es el sesgo cuadrado, el segundo es la varianza de la predicción, y al último que corresponde al error irreducible, es la varianza del error \(\epsilon|x\).

4.4 Reduciendo sesgo y varianza

En estadística y machine learning, sesgo y varianza están usualmente en tensión. Nuestros intentos por mejorar la varianza tienden a pagarse en sesgo y viceversa. Esto lo podemos ver en el análisis de datos usual: para ciertos tamaños de muestra, puede ser que prefiramos hacer una sola estimación usando toda la muestra, pero para otros quizá hacemos estimaciones individuales (por ejemplo, si se tratara de preferencia de voto). La razón es que estimaciones con grupos chicos pueden resultar en varianza alta, pero estimaciones que separan grupos diferentes están sesgadas con respecto al verdadero valor de cada grupo.

Hay varias acciones que podemos considerar para reducir el error por sesgo, o mitigar el subajuste:

• Usar un modelo más flexible (métodos como vecinos más cercanos).
• Incluir otras variables de entrada (derivadas o con nueva información), efectos no lineales, interacciones, es decir, \(p\) más grande.
• Construir modelos distintos para distintos casos (por ejemplo, un modelo para cada región).
• Quitar restricciones en el proceso de estimación.

Por otro lado para reducir el error por varianza:

• Usar un método más simple (por ejemplo, regresión lineal) o reducir el espacio de modelos posible que consideramos.
• Eliminar variables de entrada que no aportan información, quitar variables derivadas (\(p\) más chica).
• No desagregar grupos.
• Aumentar el tamaño de muestra de entrenamiento (conseguir más información, \(N\) más grande).
• Penalizar o restringir el proceso de ajuste para prevenir sobreaprendizaje.

En las secciones siguientes, veremos cómo podemos afinar la complejidad para modelos como regresión lineal y vecinos más cercanos.

Finalmente, parte del error de predicción se debe a información que no tenemos disponible para hacer nuestras predicciones (aún cuando nuestro ajuste sea perfecto). Si el error irreducible es muy grande, entonces no hay manera de afinar o seleccionar modelos para obtener desempeño aceptable: por más que intentemos, ninguna metodología o afinación nos va a ayudar a tener buenos resultados. Tener información apropiada y preprocesarla de manera correcta es el primer requisito para tener buen desempeño predictivo.

4.5 Diagnósticos de sobre y subajuste

Podemos contrastar el error de entrenamiento y el error de prueba para hacer un diagnóstico básico de sobre o subajuste. Suponiendo que los datos de prueba provienen de la misma distribución que los datos de entrenamiento, y módulo variación muestral:

• (Principalmente Subajuste) Cuando el error de entrenamiento es similar al error de prueba, y el error de entrenamiento es alto, entonces podemos considerar como sesgo el primer problema a resolver.
• (Principalmente Sobreajuste) Cuando el error de prueba es considerablemente más alto que el error de entrenamiento, pero el error de entrenamiento es satisfactorio, entonces consideramos a la varianza como el primer problema a resolver. Decimos que hay una brecha prueba-entrenamiento.
• (Combinación) El error de entrenamiento es relativamente alto, y también existe brecha considerable prueba-entrenamiento.

Esto está sujeto a dos consideraciones: si los datos de prueba son diferentes a los de entrenamiento, entonces las dos reglas de arriba pueden no cumplirse, pues hay un factor extra de error en prueba. Adicionalmente, si el tamaño de datos de prueba o entrenamiento es chico entonces tanto el error de prueba como nuestra estimación específica de error de prueba es muy variable y es difícil saber cuál de los dos problemas es el más importante.

4.6 Ejemplo: afinando k-vecinos más cercanos

Consideramos qué sucede cuando escogemos distintos valores de \(k\)-vecinos. Valores chicos de \(k\) resultan en estimaciones más ruidosas (como vimos arriba), pues promediamos pocos valores \(y\) para hacer predicciones, mientras que valores más grandes de \(k\) pueden producir sesgo pues quizá promediamos valores poco relevantes que están lejos del lugar donde queremos predecir.

En tidymodels, podemos indicar que buscamos probar varios valores de algún hiperparámetro particular con la función tune():

Ejemplo

library(gt)
auto <- read_csv("./datos/auto.csv")
datos <- auto[, c('name', 'weight','year', 'mpg', 'displacement')]
datos <- datos |> mutate(
  peso_kg = weight * 0.45359237,
  rendimiento_kpl = mpg * (1.609344 / 3.78541178), 
  año = year)

Vamos a separa en muestra de entrenamiento y de prueba estos datos. Podemos hacerlo como sigue (30% para entrenamiento aproximadamente en este caso):

library(tidymodels)
set.seed(3)
datos_particion <- initial_split(datos, prop = 0.3, strata = 5)
datos_entrena <- training(datos_particion)
datos_prueba <- testing(datos_particion)
nrow(datos_entrena)

## [1] 117

nrow(datos_prueba)

## [1] 275

Vamos a usar año y peso de los coches para predecir su rendimiento:

ggplot(datos_entrena, aes(x = peso_kg, y = rendimiento_kpl, colour = año)) +
  geom_point()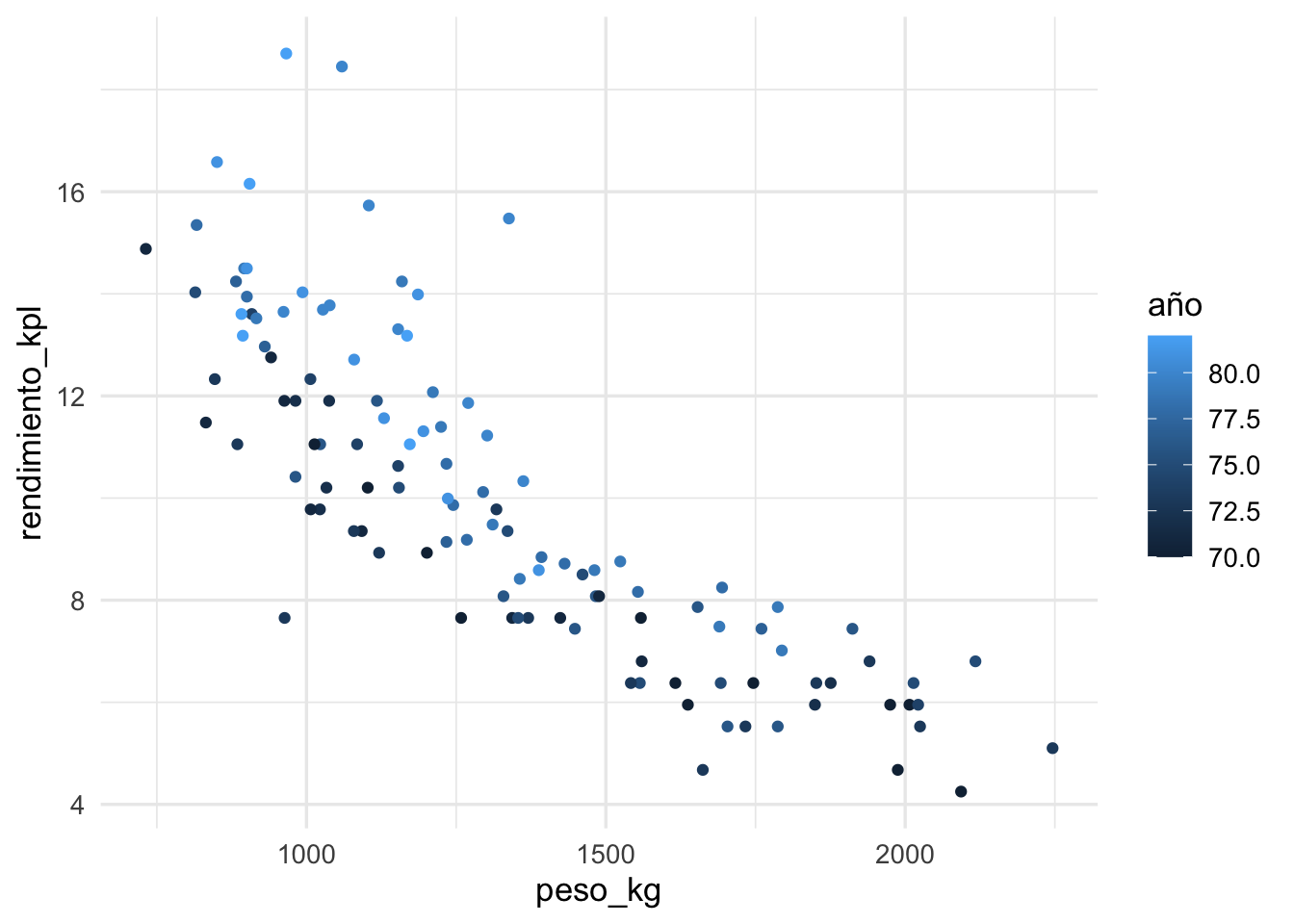

Construimos nuestra receta, donde normalizamos pues usaremos vecinos más cercanos:

receta_vmc <- recipe(rendimiento_kpl ~ peso_kg + año, datos_entrena) |> 
  step_normalize(all_predictors()) 

Probaremos con varios valores para \(k\). Para indicar esto, en la construcción del modelo indicamos los hiperparámetros que queremos probar usando la función tune:

modelo_vmc <- nearest_neighbor(neighbors = tune()) |>  
  set_engine("kknn") |>  
  set_mode("regression")

Construimos nuestro flujo:

flujo_vecinos <- workflow() |>  
  add_recipe(receta_vmc) |> 
  add_model(modelo_vmc)
flujo_vecinos

## ══ Workflow ════════════════════════════════════════════════════════════════════
## Preprocessor: Recipe
## Model: nearest_neighbor()
## 
## ── Preprocessor ────────────────────────────────────────────────────────────────
## 1 Recipe Step
## 
## • step_normalize()
## 
## ── Model ───────────────────────────────────────────────────────────────────────
## K-Nearest Neighbor Model Specification (regression)
## 
## Main Arguments:
##   neighbors = tune()
## 
## Computational engine: kknn

Y ahora definimos qué valores de vecinos queremos probar, por ejemplo

vecinos_grid <- tibble(neighbors = seq(1, 100))
#vecinos_params <- parameters(neighbors(range = c(1, 100)))
#vecinos_grid <- grid_regular(vecinos_params, levels = 100)

Ahora usamos la función tune_grid para ajustar varios modelos a la vez:

# con esta línea tune_grid reconoce qué datos usar para entrenar
# y cuáles para evaluar (que está en datos_particion)
r_split <- manual_rset(list(datos_particion), "_prueba")
vecinos_eval_tbl <- tune_grid(flujo_vecinos,
                            resamples = r_split,
                            grid = vecinos_grid,
                            metrics = metric_set(rmse)) 
res_tbl <- vecinos_eval_tbl |>
  unnest(cols = c(.metrics)) |> 
  select(id, neighbors, .metric, .estimate)
res_tbl |> head() |> gt()

id	neighbors	.metric	.estimate
_prueba	1	rmse	1.712570
_prueba	2	rmse	1.559368
_prueba	3	rmse	1.450941
_prueba	4	rmse	1.376315
_prueba	5	rmse	1.323815
_prueba	6	rmse	1.293254

Para entender mejor nuestros diagnósticos, evaluamos también el error de entrenamiento:

ggplot(res_tbl, aes(x = neighbors, y = .estimate)) +
  geom_line() + geom_point()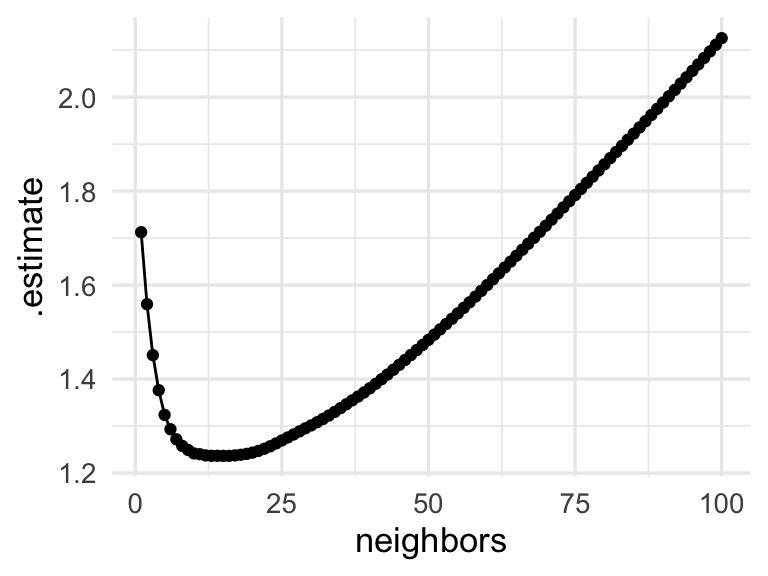

Discusión: ¿por qué crees que el desempeño predictivo tiene esta forma? ¿En qué partes parece ser más importante reducir varianza, y en cuáles el sesgo es el problema?

Calcularemos también errores de entrenamiento para cada uno de estos modelos. Como en realidad el error de entrenamiento no se usa para seleccionar modelos, es necesario escribir algo de código:

datos_1 <- bind_rows(
  datos_entrena |> mutate(id = row_number()), 
  datos_entrena |> mutate(id = nrow(datos_entrena) + row_number()))
indices_1 <- 1:nrow(datos_entrena)
indices_2 <- nrow(datos_entrena) + indices_1
part_1 <- make_splits(list("analysis" = indices_1, "assessment" = indices_2),
                      datos_1)
entrena_split <- manual_rset(list(part_1), "entrena")
vecinos_entrena_tbl <- tune_grid(flujo_vecinos,
                            resamples = entrena_split,
                            grid = vecinos_grid,
                            metrics = metric_set(rmse)) 
res_entrena_tbl <- vecinos_entrena_tbl |>
  unnest(cols = c(.metrics)) |> 
  select(id, neighbors, .metric, .estimate)
res_entrena_tbl |> head() |> gt()

id	neighbors	.metric	.estimate
entrena	1	rmse	0.0000000
entrena	2	rmse	0.4017172
entrena	3	rmse	0.6770220
entrena	4	rmse	0.8371574
entrena	5	rmse	0.9362291
entrena	6	rmse	1.0020253

ggplot(bind_rows(res_tbl, res_entrena_tbl), 
                 aes(x = neighbors, y = .estimate, group = id, colour = id)) +
  geom_line() + geom_point()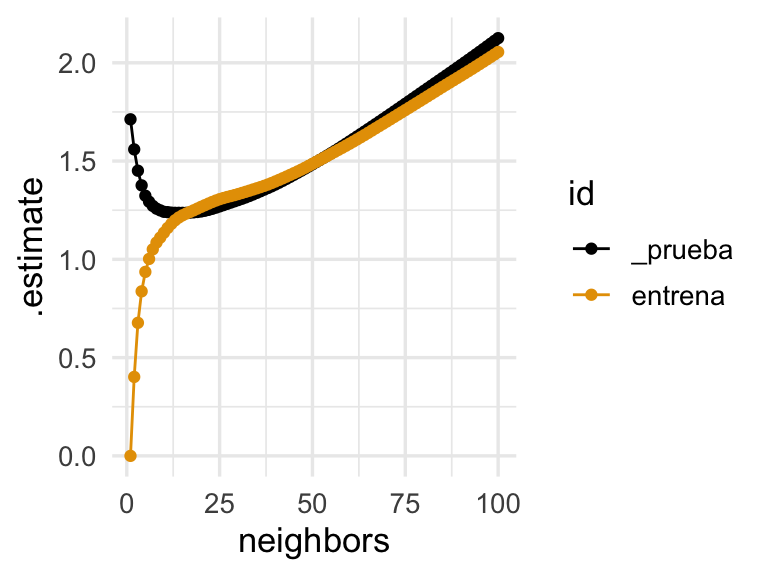

Podemos visualizar nuestro modelo seleccionado y los datos de entrenamiento de la siguiente forma:

mejor_rmse <- select_best(vecinos_eval_tbl, metric = "rmse")
ajuste_1 <- finalize_workflow(flujo_vecinos, mejor_rmse) |> 
  fit(datos_entrena)
dat_graf <- tibble(peso_kg = seq(900, 2200, by = 10)) |> 
  crossing(tibble(año = c(70, 75, 80)))
dat_graf <- dat_graf |> 
  mutate(pred_1 = predict(ajuste_1, dat_graf) |> pull(.pred))
ggplot(datos_entrena, aes(x = peso_kg, group = año, colour = año)) +
  geom_point(aes(y = rendimiento_kpl), alpha = 0.6) + 
  geom_line(data = dat_graf, aes(y = pred_1),  size = 1.2)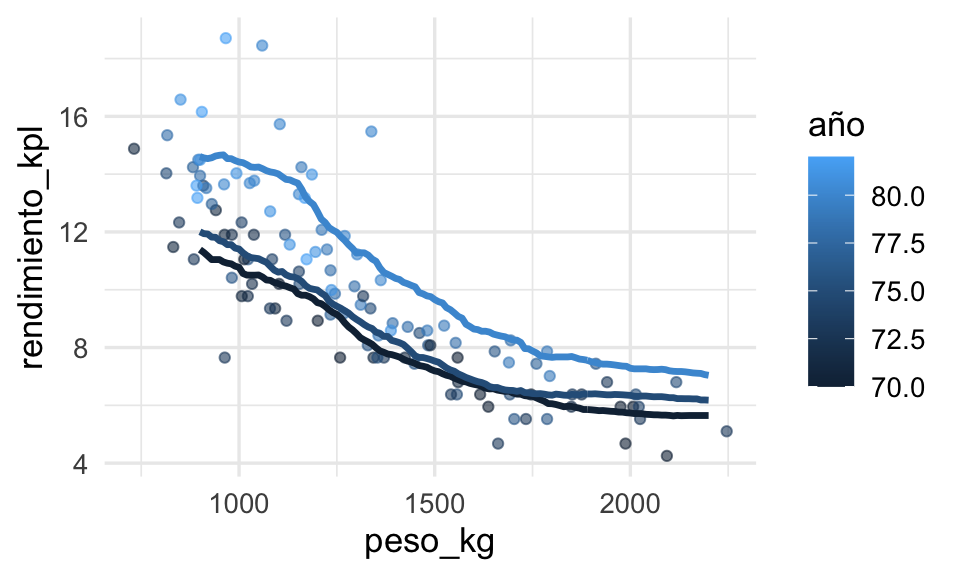

El método parece funcionar razonablemente bien para este problema simple. Sin embargo, si el espacio de entradas no es de dimensión baja, entonces podemos encontrarnos con dificultades.