7 Selección y evaluación de modelos

7.1 Entrenamiento, Validación y Prueba

El enfoque que vimos antes, en donde dividimos la muestra en dos partes al azar, es la manera más fácil de seleccionar modelos. En general, el proceso es el siguiente:

Una parte con los que ajustamos todos los modelos que nos interesa. Esta es la muestra de entrenamiento
Una parte como muestra de prueba, con el que evaluamos el desempeño de cada modelo ajustado en la parte anterior. En este contexto, a esta muestra se le llama muestra de validación}.
Posiblemente una muestra adicional independiente, que llamamos muestra de prueba, con la que hacemos una evaluación final del modelo seleccionado arriba. Es una buena idea apartar esta muestra si el proceso de validación incluye muchos métodos con varios parámetros afinados (como la \(\lambda\) de regresión ridge).

knitr::include_graphics("./figuras/div_muestra.png")

Cuando tenemos datos abundantes, este enfoque es el usual. Por ejemplo, podemos dividir la muestra en 50-25-25 por ciento. Ajustamos modelos con el primer 50%, evaluamos y seleccionamos con el segundo 25% y finalmente, si es necesario, evaluamos el modelo final seleccionado con la muestra final de 25%. Igual que mencionamos anteriormente, lo importante es que las muestras de validación sean suficientemente grandes en tamaño absoluto (número de casos) para discriminar a los mejores modelos y evaluar su error de manera apropiada

La razón de este proceso es que así podemos ir y venir entre entrenamiento y validación, buscando mejores enfoques y modelos, y no ponemos en riesgo la estimación final del error. (Pregunta: ¿por qué probar agresivamente buscando mejorar el error de validación podría ponder en riesgo la estimación final del error del modelo seleccionado? )

7.2 Validación cruzada

En muchos casos, no queremos apartar una muestra de validación para seleccionar modelos, pues no tenemos muchos datos (al dividir la muestra obtendríamos un modelo relativamente malo en relación al que resulta de todos los datos).

Un criterio para seleccionar la regularización adecuada es el de validación cruzada, que es un método computacional para producir una estimación interna (usando sólo muestra de entrenamiento) del error de predicción.

Validación cruzada también tiene nos da diagnósticos adicionales para entender la variación del desempeño según el conjunto de datos de entrenamiento que usemos, algo que es más difícil ver si solo tenemos una muestra de validación.

En validación cruzada (con \(k\) vueltas), construimos al azar una partición, con tamaños similares, de la muestra de entrenamiento \({\mathcal L}=\{ (x_i,y_i)\}_{i=1}^n\):

\[ {\mathcal L}={\mathcal L}_1\cup {\mathcal L}_2\cup\cdots\cup {\mathcal L}_k.\]

knitr::include_graphics("./figuras/div_muestra_cv.png")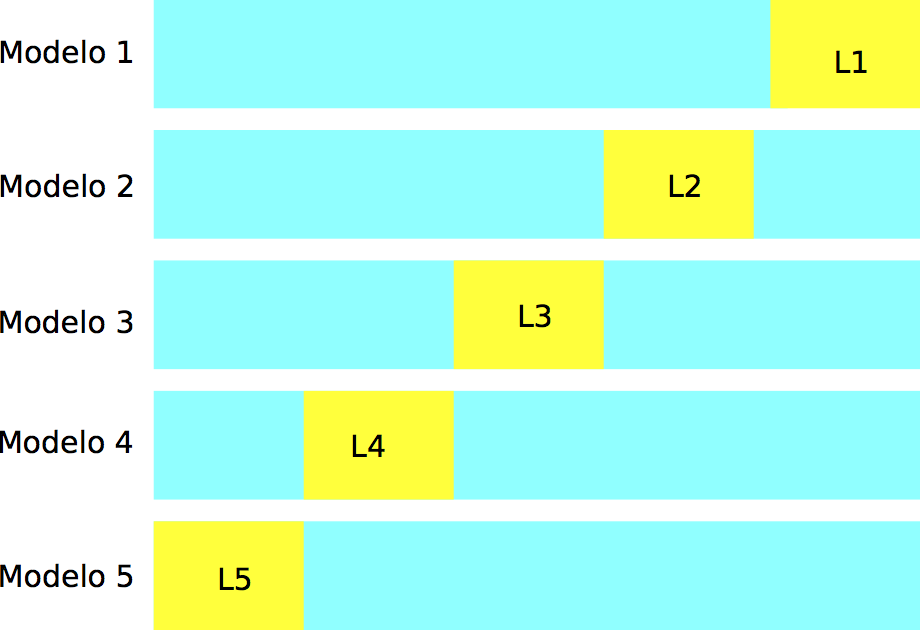

Construimos \(k\) modelos distintos, digamos \(\hat{f}_j\), usando solamente la muestra \({\mathcal L}-{\mathcal L}_j\), para \(j=1,2,\ldots, k\). Cada uno de estos modelos lo evaluamos usando la parte que no usamos para entrenarlo, \({\mathcal L}_j\), para obtener una estimación honesta del error del modelo \(\hat{f}_k\), a la que denotamos por \(\hat{e}_j\).

Notemos entonces que tenemos \(k\) estimaciones del error \(\hat{e}_1,\ldots, \hat{e}_k\), una para cada uno de los modelos que construimos. La idea ahora es que

Cada uno de los modelos \(\hat{f}_j\) es similar al modelo ajustado con toda la muestra \(\hat{f}\), de forma que podemos pensar que cada una de las estimaciones \(\hat{e}_j\) es un estimador del error de \(\hat{f}\).
Dado el punto anterior, podemos construir una mejor estimación promediando las \(k\) estimaciones anteriores, para obtener: \[\widehat{cv} = \frac{1}{k} \sum_{j=1}^k \hat{e}_j.\]
¿Cómo escoger \(k\)? Usualmente se usan \(k=5,10,20\), y \(k=10\) es el más popular. La razón es que cuando \(k\) es muy chico, tendemos a evaluar modelos construidos con pocos datos (comparado al modelo con todos los datos de entrenamiento). Por otra parte, cuando \(k\) es grande el método puede ser muy costoso (por ejemplo, si \(k=N\), hay que entrenar un modelo para cada dato de entrada).

Ejemplo

Consideremos nuestro problema de predicción de grasa corporal. Definimos el flujo de procesamiento, e indicamos qué parametros queremos afinar:

library(tidymodels)
dat_grasa <- read_csv(file = './datos/bodyfat.csv') 
set.seed(183)
grasa_particion <- initial_split(dat_grasa, 0.75)
grasa_ent <- training(grasa_particion)
grasa_pr <- testing(grasa_particion)

# nota: con glmnet no es neceario normalizar, pero aquí lo hacemos
# para ver los coeficientes en términos de las variables estandarizadas:
grasa_receta <- recipe(grasacorp ~ ., grasa_ent) |> 
  step_filter(estatura > 40) |> 
  step_normalize(all_predictors()) |> 
  prep()

modelo_regularizado <-  linear_reg(mixture = 0, penalty = 0.5) |> 
  set_engine("glmnet") 
flujo_reg <- workflow() |> 
  add_model(modelo_regularizado) |> 
  add_recipe(grasa_receta)

Y ahora construimos los cortes de validación cruzada. Haremos validación cruzada 10

set.seed(88)
validacion_particion <- vfold_cv(grasa_ent, v = 10)
# tiene información de índices en cada "fold" o "doblez" o "vuelta"
validacion_particion

## #  10-fold cross-validation 
## # A tibble: 10 × 2
##    splits           id    
##    <list>           <chr> 
##  1 <split [170/19]> Fold01
##  2 <split [170/19]> Fold02
##  3 <split [170/19]> Fold03
##  4 <split [170/19]> Fold04
##  5 <split [170/19]> Fold05
##  6 <split [170/19]> Fold06
##  7 <split [170/19]> Fold07
##  8 <split [170/19]> Fold08
##  9 <split [170/19]> Fold09
## 10 <split [171/18]> Fold10

Estimamos el error por validación cruzada

metricas_vc <- fit_resamples(flujo_reg,
  resamples = validacion_particion,
  metrics = metric_set(rmse, mae, rsq)) 
metricas_vc |> unnest(.metrics)

## # A tibble: 30 × 7
##    splits           id     .metric .estimator .estimate .config       .notes    
##    <list>           <chr>  <chr>   <chr>          <dbl> <chr>         <list>    
##  1 <split [170/19]> Fold01 rmse    standard       6.75  Preprocessor… <tibble […
##  2 <split [170/19]> Fold01 mae     standard       5.05  Preprocessor… <tibble […
##  3 <split [170/19]> Fold01 rsq     standard       0.735 Preprocessor… <tibble […
##  4 <split [170/19]> Fold02 rmse    standard       4.94  Preprocessor… <tibble […
##  5 <split [170/19]> Fold02 mae     standard       4.02  Preprocessor… <tibble […
##  6 <split [170/19]> Fold02 rsq     standard       0.689 Preprocessor… <tibble […
##  7 <split [170/19]> Fold03 rmse    standard       3.66  Preprocessor… <tibble […
##  8 <split [170/19]> Fold03 mae     standard       3.05  Preprocessor… <tibble […
##  9 <split [170/19]> Fold03 rsq     standard       0.678 Preprocessor… <tibble […
## 10 <split [170/19]> Fold04 rmse    standard       3.93  Preprocessor… <tibble […
## # … with 20 more rows

Vemos que esta función da un valor del error para cada vuelta de validación cruzada:

metricas_vc |> unnest(.metrics) |>  group_by(.metric) |> count()

## # A tibble: 3 × 2
## # Groups:   .metric [3]
##   .metric     n
##   <chr>   <int>
## 1 mae        10
## 2 rmse       10
## 3 rsq        10

Para resumir, como explicamos arriba, podemos resumir con media y error estándar:

metricas_resumen <- metricas_vc |> 
  collect_metrics()
metricas_resumen

## # A tibble: 3 × 6
##   .metric .estimator  mean     n std_err .config             
##   <chr>   <chr>      <dbl> <int>   <dbl> <chr>               
## 1 mae     standard   3.80     10  0.176  Preprocessor1_Model1
## 2 rmse    standard   4.75     10  0.263  Preprocessor1_Model1
## 3 rsq     standard   0.727    10  0.0159 Preprocessor1_Model1

Nótese que la estimación del error de predicción por validación cruzada incluye un error de estimación (intervalos).

7.3 ¿Qué incluir en la validación cruzada?

Un principio importante que debemos seguir cuando hacemos validación cruzada es el siguiente:

En cada vuelta de validación cruzada, se deben repetir todos los pasos de preprocesamiento para cada subdivisión de los datos.
Un error común que invalida la estimación de validación cruzada es preprocesar primero los datos, y luego hacer validación cruzada sobre los datos preprocesados.
Esto es especialmente crítico cuando el preprocesamiento utiliza la variable respuesta para construir o filtrar variables de entrada (por ejemplo, decidir cortes, filtrar por correlación, etc.)

Un caso dramático de este problema puede verse en el siguiente ejemplo:

Supongamos que tenemos una respuesta \(y\) independiente de las entradas \(x\), de forma que la mejor predicción que podemos hacer es la media de la \(y\), cuyo error cuadrático es la varianza de \(y\). Tenemos una gran cantidad de entradas y relativamente pocos casos:

set.seed(112)
x <- rnorm(50 * 10000, 0, 1) |> matrix(nrow = 50, ncol = 10000)
# y es independiente de las x's:
y <- rnorm(50, 0 , 10) 
sd(y)

## [1] 10.2887

Supongamos que queremos construir un modelo pero consideramos que tenemos “demasiadas” variables de entrada. Decidimos entonces seleccionar solamente las 10 variables que más relacionadas con \(y\).

correlaciones <- cor(x, y) |> as.numeric()
orden <- order(correlaciones, decreasing = TRUE)
seleccionadas <- orden[1:10]
correlaciones[seleccionadas] |> round(2)

##  [1] 0.57 0.49 0.49 0.48 0.46 0.44 0.44 0.44 0.43 0.43

Una vez que seleccionamos las variables hacemos validación cruzada con un modelo lineal (nota: esto es un error!)

datos <- as_tibble(x[, seleccionadas]) |> 
  mutate(y = y)

## Warning: The `x` argument of `as_tibble.matrix()` must have unique column names if `.name_repair` is omitted as of tibble 2.0.0.
## Using compatibility `.name_repair`.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_lifecycle_warnings()` to see where this warning was generated.

vc_particion <- vfold_cv(datos, v = 10)
modelo_lineal <- linear_reg() 
flujo <- workflow() |> add_model(modelo_lineal) |> add_formula(y ~ .)
resultados <- fit_resamples(flujo, resamples = vc_particion, metrics = metric_set(rmse)) |> 
  collect_metrics()
resultados

## # A tibble: 1 × 6
##   .metric .estimator  mean     n std_err .config             
##   <chr>   <chr>      <dbl> <int>   <dbl> <chr>               
## 1 rmse    standard    5.29    10   0.702 Preprocessor1_Model1

La estimación del error es demasiado baja.

#devtools::install_github("stevenpawley/recipeselectors")
library(recipeselectors)
# esta función es una modificación simple de step_select_roc
source("R/step_select_corr.R")

Si incluimos la selección de variables en la receta, entonces en cada corte de validación cruzada seleccionamos las variables que tienen correlación más alta:

datos_completos <- as_tibble(x) |> mutate(y = y) 
vc_particion_comp <- vfold_cv(datos_completos, v = 10)
receta_mala <- recipe(y ~ ., data = datos_completos) |> 
  step_select_corr(all_predictors(), outcome = "y", top_p = 10)
flujo <- workflow() |> 
  add_recipe(receta_mala) |> 
  add_model(modelo_lineal) 
resultados <- fit_resamples(flujo, resamples = vc_particion_comp, metrics = metric_set(rmse)) |> 
  collect_metrics()
resultados

## # A tibble: 1 × 6
##   .metric .estimator  mean     n std_err .config             
##   <chr>   <chr>      <dbl> <int>   <dbl> <chr>               
## 1 rmse    standard    10.3    10    1.02 Preprocessor1_Model1

Y vemos que esta estimación es consistente con que la desviación estándar de \(y\) es igual a 10.

Tidymodels en general está construido para promover buenas práticas y evitar en lo posible estos errores en la validación cruzada. Al ajustar flujos que incluyen recetas de preprocesamineto, todos los pasos se aplican en cada vuelta de validación cruzada de manera indepediente.

7.4 Afinación de hiperparámetros (intro)

Cuando tenemos una división entrena-validación-prueba, podemos usar validación para afinar hiperparámetros de los modelos que ajustamos (por ejemplo, cuánta regularización). Si tenemos una división entrena-prueba, podemos usar validación cruzada para hacer esa afinación.

Consideremos el ejemplo de grasa corporal:

library(tidymodels)
dat_grasa <- read_csv(file = './datos/bodyfat.csv') 
set.seed(183)
grasa_particion <- initial_split(dat_grasa, 0.7)
grasa_ent <- training(grasa_particion)
grasa_pr <- testing(grasa_particion)

grasa_receta <- recipe(grasacorp ~ ., grasa_ent) |> 
  step_filter(estatura > 40) |> 
  step_center(all_numeric_predictors())

Usamos la función tune() para indicar que queremos probar varios valores

# con tune() indicamos que ese parámetro será afinado
modelo_regularizado <-  linear_reg(mixture = tune(), penalty = tune()) |> 
  set_engine("glmnet") |> 
  set_args(lambda.min.ratio = 1e-20)
flujo_reg <- workflow() |> 
  add_model(modelo_regularizado) |> 
  add_recipe(grasa_receta)

Preparamos nuestro conjunto de particiones de validación cruzada:

set.seed(88)
validacion_particion <- vfold_cv(grasa_ent, v = 10)
# tiene información de índices en cada "fold" o "doblez" o "vuelta"

Y especificamos que parámetros queremos probar, haciendo todas las combinaciones posibles:

hiper_param <- crossing(mixture = c(0.0, 0.25, 0.5, 0.75, 1.0),
                        penalty = 10^seq(-3, 2, 0.5))
hiper_param

## # A tibble: 55 × 2
##    mixture  penalty
##      <dbl>    <dbl>
##  1       0  0.001  
##  2       0  0.00316
##  3       0  0.01   
##  4       0  0.0316 
##  5       0  0.1    
##  6       0  0.316  
##  7       0  1      
##  8       0  3.16   
##  9       0 10      
## 10       0 31.6    
## # … with 45 more rows

Y ajustamos con cada combinación, estimando el error por validación cruzada

metricas_vc <- tune_grid(flujo_reg,
  resamples = validacion_particion,
  grid = hiper_param,
  metrics = metric_set(rmse, mae)) 
metricas_vc |> unnest(.metrics)

## # A tibble: 1,100 × 9
##    splits   id     penalty mixture .metric .estimator .estimate .config  .notes 
##    <list>   <chr>    <dbl>   <dbl> <chr>   <chr>          <dbl> <chr>    <list> 
##  1 <split … Fold01 1   e-3       0 rmse    standard        3.15 Preproc… <tibbl…
##  2 <split … Fold01 3.16e-3       0 rmse    standard        3.15 Preproc… <tibbl…
##  3 <split … Fold01 1   e-2       0 rmse    standard        3.15 Preproc… <tibbl…
##  4 <split … Fold01 3.16e-2       0 rmse    standard        3.18 Preproc… <tibbl…
##  5 <split … Fold01 1   e-1       0 rmse    standard        3.26 Preproc… <tibbl…
##  6 <split … Fold01 3.16e-1       0 rmse    standard        3.46 Preproc… <tibbl…
##  7 <split … Fold01 1   e+0       0 rmse    standard        3.86 Preproc… <tibbl…
##  8 <split … Fold01 3.16e+0       0 rmse    standard        4.59 Preproc… <tibbl…
##  9 <split … Fold01 1   e+1       0 rmse    standard        5.64 Preproc… <tibbl…
## 10 <split … Fold01 3.16e+1       0 rmse    standard        6.68 Preproc… <tibbl…
## # … with 1,090 more rows

collect_metrics(metricas_vc) |> 
  filter(.metric == "rmse") |> 
ggplot(aes(x = penalty, y = mean, ymin = mean - std_err, ymax = mean + std_err, 
           group = mixture, colour = factor(mixture))) +
  geom_line() + geom_linerange() + geom_point() + scale_x_log10()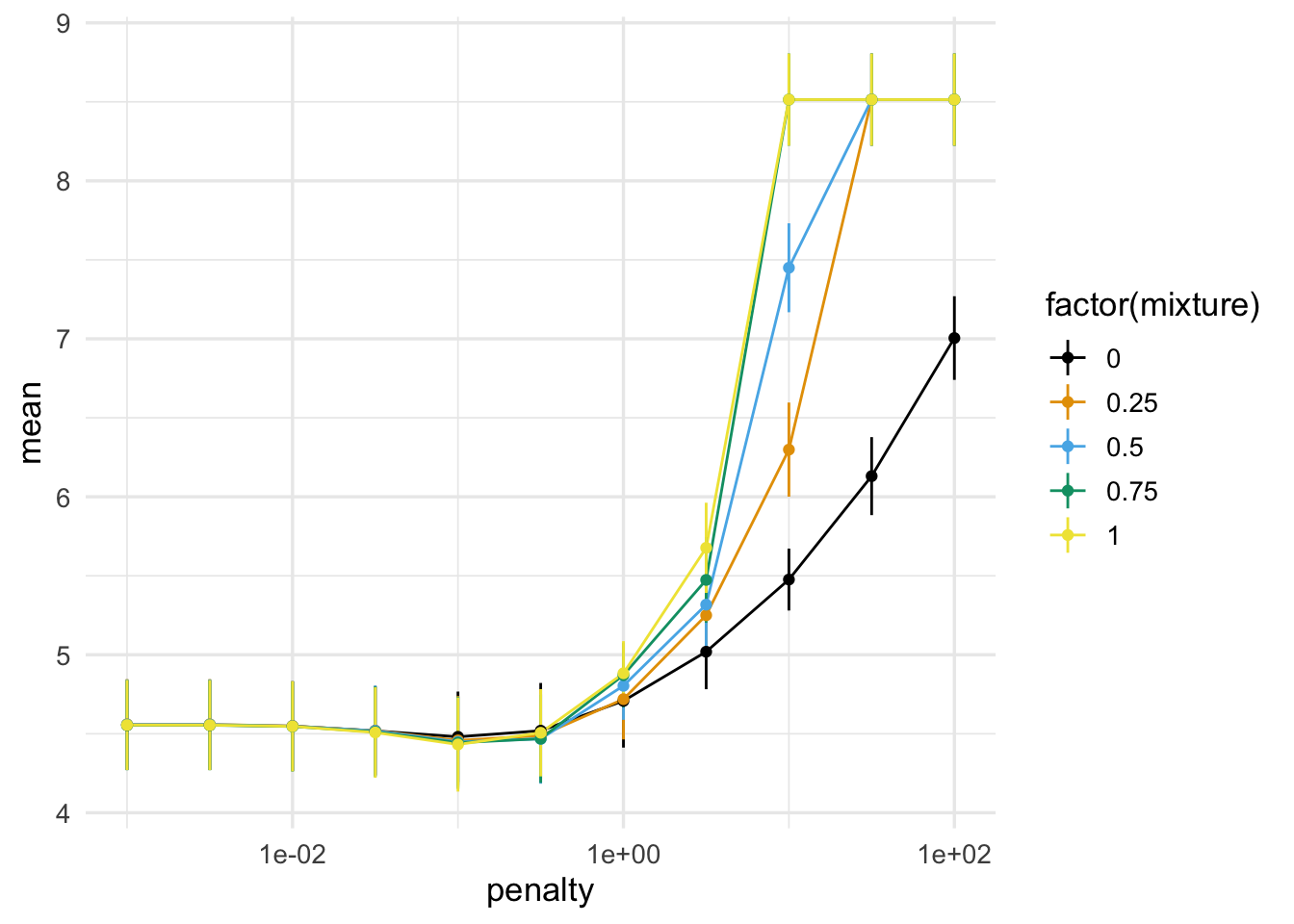

Podemos mostrar los mejores modelos como sigue:

show_best(metricas_vc, n = 3, metric = "rmse")

## # A tibble: 3 × 8
##   penalty mixture .metric .estimator  mean     n std_err .config              
##     <dbl>   <dbl> <chr>   <chr>      <dbl> <int>   <dbl> <chr>                
## 1     0.1    1    rmse    standard    4.43    10   0.298 Preprocessor1_Model49
## 2     0.1    0.75 rmse    standard    4.44    10   0.292 Preprocessor1_Model38
## 3     0.1    0.5  rmse    standard    4.45    10   0.285 Preprocessor1_Model27

En este caso, vemos que valores mixture no es muy importante cuando escogemos la penalización adecuada. Usaremos el modelo con mejor resultados, y ahora podemos finalizar nuestro ajuste:

flujo_ajustado <- 
  finalize_workflow(flujo_reg, 
                    parameters = select_best(metricas_vc, metric = "rmse")) |> 
  fit(grasa_ent)

Nuestro modelo final es:

library(gt)
flujo_ajustado |> extract_fit_parsnip() |> tidy() |> 
  filter(estimate != 0) |> 
  mutate(estimate = round(estimate, 4)) |> 
  select(-penalty) |> gt()

term	estimate
(Intercept)	19.1417
edad	0.0442
peso	-0.0232
cuello	-0.4016
abdomen	0.8036
cadera	-0.0001
tobillo	-0.2553
biceps	0.0610
antebrazo	0.3883
muñeca	-1.6709

Podemos también seleccionar un modelo ligeramente más regularizado, consistente con los resultados del mejor:

flujo_ajustado <- 
  finalize_workflow(flujo_reg, 
    parameters = 
      select_by_one_std_err(metricas_vc, metric = "rmse", desc(penalty))) |> 
  fit(grasa_ent)

Nuestro modelo final es:

flujo_ajustado |> extract_fit_parsnip() |> tidy() |> 
  filter(estimate != 0) |> 
  mutate(estimate = round(estimate, 4)) |> 
  select(-penalty) |> gt()

term	estimate
(Intercept)	19.1417
edad	0.0899
peso	0.0069
estatura	-0.1526
cuello	-0.3950
pecho	0.1715
abdomen	0.4288
cadera	0.0689
muslo	0.1666
rodilla	0.1903
tobillo	-0.4010
biceps	0.0811
antebrazo	0.3187
muñeca	-1.5680

Y finalmente, veamos su desempeño en prueba:

predict(flujo_ajustado, grasa_pr) |> 
  bind_cols(grasa_pr |> select(grasacorp)) |> 
  ggplot(aes(x = .pred, y = grasacorp)) +
  geom_point() + geom_abline() +
  coord_obs_pred()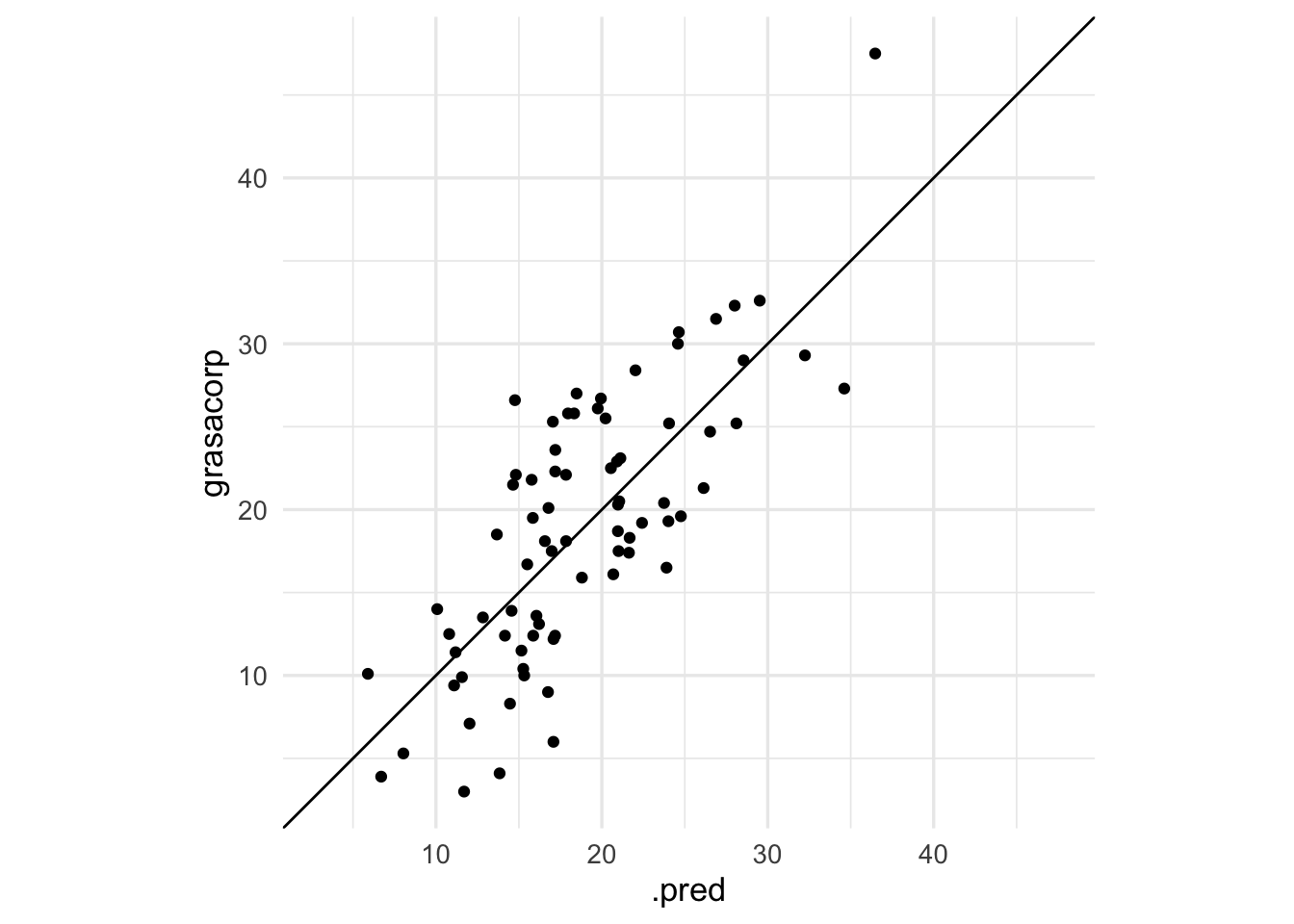

7.5 ¿Cómo se desempeña validación cruzada como estimación del error?

Podemos comparar el desempeño estimado con validación cruzada con el de muestra de prueba: Consideremos nuestro ejemplo simulado de regresión logística. Repetiremos varias veces el ajuste y compararemos el error de prueba con el estimado por validación cruzada:

set.seed(28015)
a_vec <- rnorm(50, 0, 0.2)
a <- tibble(term = paste0('V', 1:length(a_vec)), valor = a_vec)
modelo_1 <- linear_reg(penalty = 0.01) |> 
    set_engine("glmnet", lambda.min.ratio = 1e-20) 
flujo_1 <- workflow() |> 
    add_model(modelo_1) |> 
    add_formula(y ~ .)
sim_datos <- function(n, beta){
  p <- nrow(beta)
  mat_x <- matrix(rnorm(n * p, 0, 0.5), n, p) + rnorm(n) 
  colnames(mat_x) <- beta |> pull(term)
  beta_vec <- beta |> pull(valor)
  f_x <- (mat_x %*% beta_vec) 
  y <- as.numeric(f_x) + rnorm(n, 0, 1)
  datos <- as_tibble(mat_x) |> 
    mutate(y = y) 
  datos
}
simular_evals <- function(rep, flujo, beta){
  datos <- sim_datos(n = 4000, beta = beta)
  particion <- initial_split(datos, 0.05)
  datos_ent <- training(particion)
  datos_pr <- testing(particion)
  # evaluar con muestra de prueba
  metricas <- metric_set(rmse)
  flujo_ajustado <- flujo_1 |> fit(datos_ent)
  eval_prueba <- predict(flujo_ajustado, datos_pr) |> 
    bind_cols(datos_pr |> select(y)) |> 
    metricas(y, .pred)
  eval_entrena <- predict(flujo_ajustado, datos_ent) |> 
    bind_cols(datos_ent |> select(y)) |> 
    metricas(y, .pred)
  # particionar para validación cruzada
  particiones_val_cruzada <- vfold_cv(datos_ent, v = 5)
  eval_vc <- flujo_1 |> 
    fit_resamples(resamples = particiones_val_cruzada, metrics = metricas) |> 
    collect_metrics()
  res_tbl <- 
    eval_prueba |> mutate(tipo = "prueba") |> 
    bind_rows(eval_entrena |> mutate(tipo = "entrenamiento")) |> 
    bind_rows(eval_vc |> 
              select(.metric, .estimator, .estimate = mean) |> 
              mutate(tipo = "val_cruzada"))
}

set.seed(82853)
evals_tbl <- tibble(rep = 1:20) |> 
  mutate(data = map(rep, ~ simular_evals(.x, flujo_1, beta = a))) |> 
  unnest(data)

ggplot(evals_tbl |> 
        filter(.metric == "rmse") |> 
        pivot_wider(names_from = tipo, values_from = .estimate) |> 
        pivot_longer(cols = c(entrenamiento, val_cruzada), names_to = "tipo"), 
       aes(x = prueba, y = value)) +
  geom_point() + facet_wrap(~ tipo) +
  geom_abline(colour = "red") + 
  xlab("Error de predicción (prueba)") +
  ylab("Error") +
  coord_obs_pred()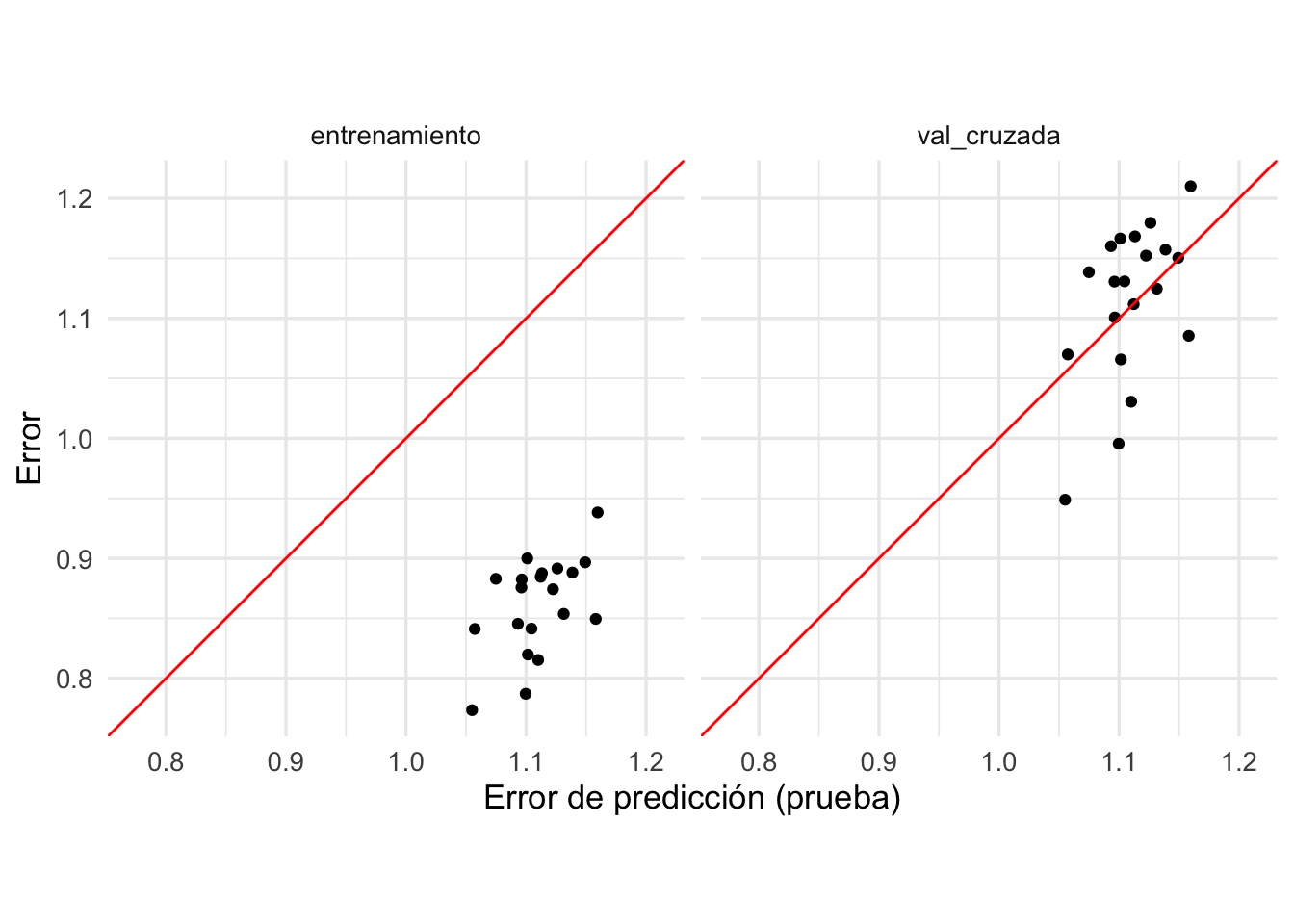

En primer lugar, vemos que el error de entrenamiento subestima considerablemente al error de predicción. En la segunda gráfica notamos que el error de prueba y la estimación de validación cruzada están centradas en lugares similares. De estas dos observaciones concluimos en primer lugar que usar la estimación de validación cruzada para estimar el error de predicción es mejor que simplemente tomar el error de entrenamiento.

La segunda observación es que el error por validación cruzada no está muy correlacionado con el error de prueba, aún cuando están centrados en lugares similares, de modo que no parece evaluar apropiadamente el modelo particular que ajustamos en cada caso.

Sin embargo, cuando usamos validación cruzada para seleccionar modelos tenemos lo siguiente:

set.seed(859)
datos <- sim_datos(n = 4000, beta = a[1:40, ])
modelo <- linear_reg(mixture = 0, penalty = tune()) |> 
  set_engine("glmnet", lambda.min.ratio = 1e-20) 
flujo <- workflow() |> 
    add_model(modelo) |> 
    add_formula(y ~ .)
# crear partición de análisis y evaluación
particion_val <- validation_split(datos, 0.05)
candidatos <- tibble(penalty = exp(seq(-5, 5, 1)))
# evaluar
val_resultado <- tune_grid(flujo, resamples = particion_val, grid = candidatos,
                       metrics = metric_set(rmse)) |> 
  collect_metrics() |> 
  select(penalty, .metric, mean) |> 
  mutate(tipo ="datos de validación")

# extraer datos de entrenamiento
set.seed(834)
datos_ent <- analysis(particion_val$splits[[1]])
particion_vc <- vfold_cv(datos_ent, v = 10)
val_c_resultado <- tune_grid(flujo, resamples = particion_vc, grid = candidatos,
                         metrics = metric_set(rmse)) |> 
  collect_metrics() |>
  select(penalty, .metric, mean) |> 
  mutate(tipo = "validación cruzada")

comparacion_val <- bind_rows(val_resultado, val_c_resultado) |> 
  filter(.metric == "rmse")
ggplot(comparacion_val, aes(x = penalty, y = mean, colour = tipo)) +
  geom_line() + geom_point() +
  facet_wrap(~.metric) +
  scale_x_log10()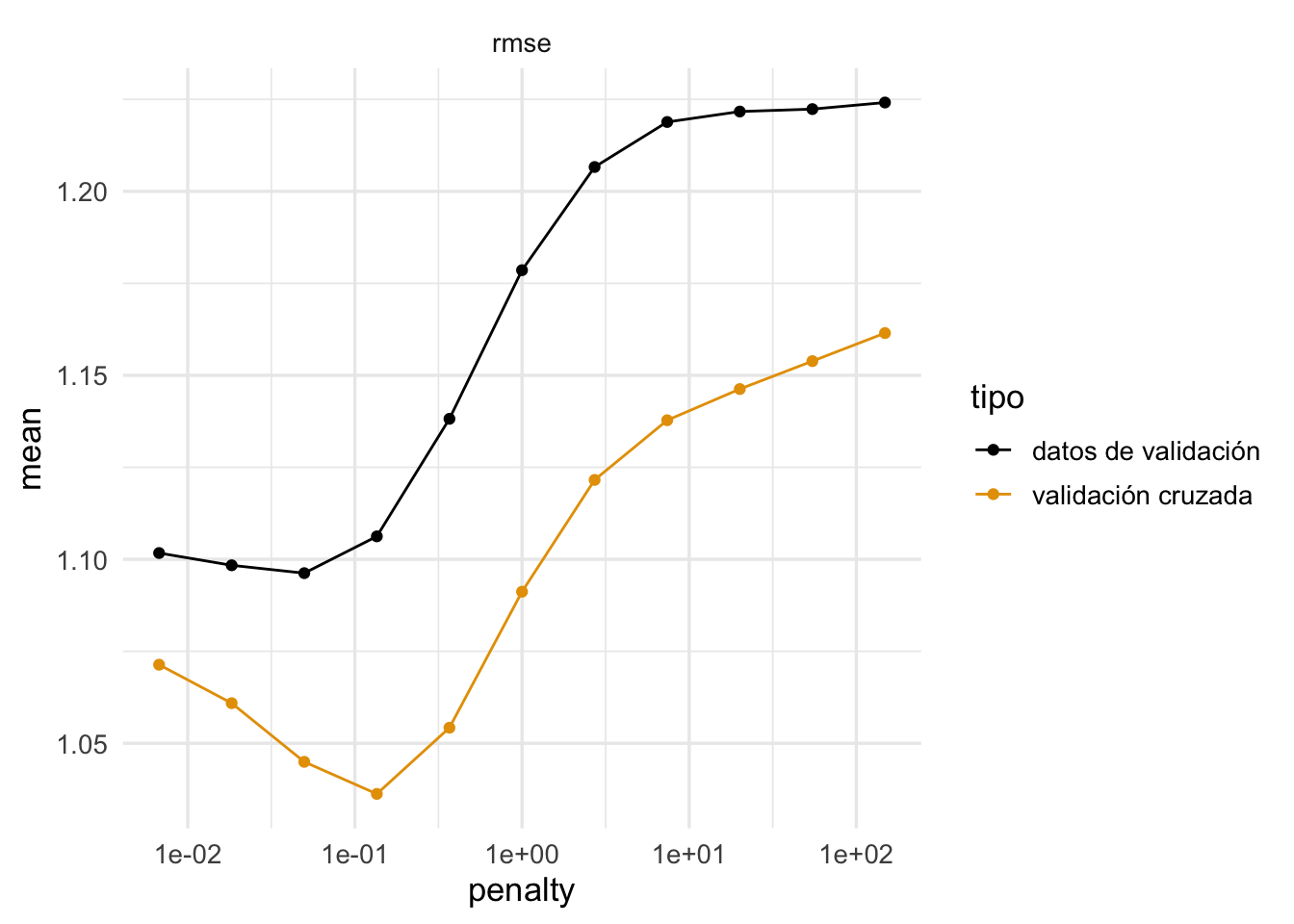

Vemos que la estimación en algunos casos no es tan buena, aún cuando todos los datos fueron usados. Pero el mínimo se encuentra en lugares similares. La razón es:

Validación cruzada en realidad considera perturbaciones del conjunto de entrenamiento, de forma que lo que intenta evaluar es el error producido, para cada lambda, sobre distintas muestras de entrenamiento. En realidad nosotros queremos evaluar el error de predicción del modelo que ajustamos. Validación cruzada es más un estimador del error esperado de predicción sobre los modelos que ajustaríamos con distintas muestras de entrenamiento.

El resultado es que:

Usamos validación cruzada para escoger la complejidad adecuada de la familia de modelos que consideramos.
Como estimación del error de predicción del modelo que ajustamos, validación cruzada es más seguro que usar el error de entrenamiento, que muchas veces puede estar fuertemente sesgado hacia abajo. Sin embargo, lo mejor en este caso es utilizar una muestra de prueba.
Existen variaciones (validación cruzada anidada, puedes ver el paper, y está implementado en tidymodels con la función nested_cv) que aún cuando es más exigente computacionalmente, produce mejores resultados cuando queremos utilizarla como estimación del error de prueba.
Estratificación: especialmente en casos donde queremos predecir una variable categórica con algunas clases muy minoritarias, o cuando la respuesta tiene colas largas, puede ser buena idea estratificar la selecciones de muestra de prueba y las muestras de validación cruzada, de manera que cada corte es similar en composición de la variable respuesta. Esto es para evitar variación debida a la composición de muestras de validación, especialmente cuando la muestra de entrenamiento es relativamente chica.

7.6 Validación cruzada repetida

Con el objeto de reducir la varianza de las estimaciones por validación cruzada, podemos repetir varias veces usando distintas particiones seleccionadas al azar.

Por ejemplo, podemos repetir 5 veces validación cruzada con 10 vueltas, y ajustamos un total de 50 modelos. Esto no es lo mismo que validación cruzada con 50 vueltas. Hay razones para no subdividir tanto la muestra de entrenamiento:

Aunque esquemas de validación cruzada-\(k\) con \(k\) grande pueden ser factibles, estos no se favorecen por la cantidad de cómputo necesaria y porque presentan sesgo hacia modelos más complejos (Shao 1993).
En el extremo, podemos hacer validación leave-one-out (LOOCV)
En estudios de simulación se desempeñan mejor métodos con \(k=5, 10, 20\), y cuando es posible, es mejor usar repeticiones

6 Regularizacion: controlando complejidad

8 Problemas de clasificación