3 La tarea predictiva fundamental

En esta parte discutiremos en qué consiste el aprendizaje supervisado, cómo medimos el desempeño de nuestras predicciones, y cómo entender este desempeño en el contexto del problema que queremos resolver.

3.1 Aprendizaje supervisado

El objetivo principal en el aprendizaje supervisado es

Usar datos etiquetados para construir modelos
Usar estos modelos para hacer predicciones precisas de nuevos casos

En función de esto, definimos la siguiente notación. Tenemos datos de entrenamiento de la forma \[(x^{(i)}, y^{(i)}) = \left ( (x_1^{(i)}, x_2^{(i)}, \ldots, x_p^{(i)}), y^{(i)} \right)\] a \(x_1, x_2, \ldots, x_p\) les llamamos variables de entrada, y \(y\) es la respuesta. El conjunto de entrenamiento es

\[{\mathcal L} = (x^{(1)}, y^{(1)}), (x^{(2)}, y^{(2)}), \ldots, (x^{(N)}, y^{(N)}) \] Usando estos datos, buscamos construir una función

\[{\mathcal L} \to \hat{f} = f_{\mathcal L}\].

Si observamos en el futuro un nuevo caso con variables de entrada \(\mathbf{x} = (\mathbf{x}_1, \ldots, \mathbf{x}_p)\), nuestra predicción sería

\[\hat{\mathbf{y}} = \hat{f} (\mathbf{x}),\]

y una vez que conocemos el verdadero valor \(\mathbf{y}\) de la variable respuesta, quisiéramos que nuestra predicción \(\hat{\mathbf{y}}\) esté cercana al verdadero valor \(\mathbf{y}\). La definición de cercana puede depender del problema particular.

Típicamente nos interesa hacer más de una predicción individual, y evaluar el desempeño en una población dada para la cual no conocemos la respuesta. Así que quisiéramos evaluar varios casos nuevos, que de preferencia son una muestra grande del universo de datos para los que nos interesa hacer predicciones. Para esto necesitamos un conjunto de datos de prueba suficientemente grande y representativo, que denotamos por:

\[{\mathcal T} = (\mathbf{x}^{(1)}, \mathbf{y}^{(1)}), (\mathbf{x}^{(2)}, \mathbf{y}^{(2)}), \ldots, (\mathbf{x}^{(m)}, \mathbf{y}^{(m)}),\]

Al principio no conocemos la respuesta \(\mathbf{y}^{(i)}\) así que hacemos las predicciones \[\hat{\mathbf{y}}^{(i)} = \hat{f}(\mathbf{x}^{(i)}).\]

Finalmente, una vez que conocemos los valores de la respuesta verdaderos, medimos el desempeño de nuestro modelo comparando \(\hat{\mathbf{y}}^{(i)}\) con \({\mathbf{y}}^{(i)}\), por ejemplo, analizando o resumiendo los residuales:

\[\hat{\mathbf{y}}^{(i)}-{\mathbf{y}}^{(i)}.\] Si en general estos valores están cercanos, entonces consideramos que nuestras predicciones son buenas.

3.2 Medidas de error de predicción

Hay varias maneras de medir el error de cada predicción particular. Es común, por ejemplo, usar el error cuadrático \[L({\mathbf{y}}^{(i)}, \hat{\mathbf{y}}^{(i)}) = \left ( {\mathbf{y}}^{(i)} - \hat{\mathbf{y}}^{(i)} \right )^2\] o también el error absoluto \[L({\mathbf{y}}^{(i)}, \hat{\mathbf{y}}^{(i)}) = \left | {\mathbf{y}}^{(i)} - \hat{\mathbf{y}}^{(i)} \right |\]

A partir de estas medidas (o funciones de pérdida como a veces se llaman), podemos definir el error de prueba \(\hat{Err}\) como el promedio de error sobre los datos de prueba. Por ejemplo, para el error absoluto calcularíamos:

\[\hat{Err} = \frac{1}{m}\sum_i \left | {\mathbf{y}}^{(i)} - \hat{\mathbf{y}}^{(i)} \right |\]

Este tipo de medidas promedio es adecuado cuando hacemos muchas predicciones, y tiene sentido usar el promedio como medida general del desempeño predictivo. Cuando sólo queremos hacer unas cuantas predicciones importantes, típicamente es necesario hacer una cuantificación más detallada de lo que puede suceder para distintas predicciones (por ejemplo usando intervalos de confianza o probabilidad, como veremos más adelante).

Con el conjunto de datos de entrenamiento construimos nuestra función de predicción \(\hat{f}\).
Con el conjunto de datos de prueba evaluamos el desempeño predictivo de nuestro modelo. Este desempeño puede resumirse como un promedio de nuestra medida de error sobre cada caso.
El conjunto de datos de prueba no debe ser utilizado en la construcción de la función de predicción \(\hat{f}\)
No tiene sentido usar los datos de prueba para construir la función de predictor: los casos de prueba son análogos a las preguntas de un examen. Los datos de entrenamiento son los casos que “mostramos” al modelo para aprender a contestar esas preguntas
El error de entrenamiento está sesgado hacia abajo como estimador del desempeño predictivo.

3.3 Ejemplo: Kaggle

En la plataforma Kaggle, los concursos de predicción siguen esta forma: se entregan a los concursantes datos etiquetados (es decir, los pares de entrenamiento \((x^{(i)}, y^{(i)})\)), y además las entradas de prueba \(\mathbf{x}^{(j)}\), pero no saben las etiquetas o valores verdaderos \(\mathbf{y}^{(i)}\). Los concursantes aplican sus algoritmos a los datos de entrenamiento, y entregan predicciones \(f(\mathbf{x}^{(j)})\) para las entradas de prueba. Kaggle se encarga de comparar esas predicciones con los valores reales que sólo Kaggle conoce.

3.4 Flujo básico de trabajo

Para construir modelos predictivos tendremos un conjunto de datos etiquetados. Un flujo básico (en general necesitaremos un proceso más complejo) podría ser el siguiente:

Preprocesamiento y modelos

Dividimos la muestra en dos partes: entrenamiento y prueba.
Exploramos e investigamos los datos de entrenamiento.
Limpiamos y preprocesamos los datos de entrenamiento, y definimos todos los pasos de preprocesamiento de manera precisa.
Ajustamos uno o varios modelos \(f\) para hacer predicciones.

Evaluación

Aplicamos el mismo preprocesamiento que ya tenemos a los **datos de prueba (no podemos modificarlo según datos de prueba)
Aplicamos nuestro modelo fijo \(f\) (que no podemos modificar según datos de prueba) a las entradas de prueba
Comparamos las predicciones de nuestro modelo con la respuesta verdadera de los datos de prueba.

La exploración, preprocesamiento y modelo no pueden depender de ninguna forma de los datos de prueba
La condición principal que buscamos en la división de entrenamiento y prueba es que tengamos suficientes datos de prueba para tener una evaluación razonablemente precisa del desempeño predictivo. Esto implica que en términos absolutos debe ser suficientemente grande.

3.5 Flujo básico en tidymodels

Primero ilustramos las funciones que utilizaremos para construir nuestros modelos según el patrón explicado arriba. Supondremos para empezar que queremos predecir el precio por metro cuadrado de las casas usando solamente la variable de calidad de acabados y area habitable por metro cuadrado. Queremos usar un modelo lineal ajustados con mínimos cuadrados, es decir, si las variables \(x_1,x_2,\ldots, x_p\) son las entradas, nuestro predictor es de la forma

\[f(x) = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \cdots + \beta_p x_p.\] Los valores de las \(\beta\)’s los encontraremos minimizando el error cuadrático medio sobre la muestra de entrenamiento.

Partición de datos

Cargamos los datos y verificamos cuántos datos tenemos disponibles:

library(tidymodels)
library(gt)
source("R/casas_traducir_geo.R")
casas <- casas |> filter(condicion_venta == "Normal")
nrow(casas)

## [1] 1198

En este ejemplo, decidimos usar 70% de los datos para entrenar, lo que nos da alrededor de 350 casos para prueba. Discutiremos al final cómo llegamos a esta proporción:

set.seed(8834)
casas_particion <- initial_split(casas, prop = 0.7)
entrena_casas <- training(casas_particion)

Análisis conceptual y exploración

Ahora podemos explorar y decidir cómo tratar los datos de entrenamiento con la idea de producir buenos predictores, lo que incluye cómo limpiamos datos, validamos sus valores, y si es necesario reexpresar ciertas variables. Sólo utilizamos los datos de entrenamiento, y usamos nuestras herramientas usuales de análisis. Por ejemplo, hacemos algunos resúmenes:

library(skimr)
skim(entrena_casas |> select(precio_m2_miles, calidad_gral,
                              area_hab_m2))

Table 3.1: Data summary
Name	select(entrena_casas, pre…
Number of rows	838
Number of columns	3
_______________________
Column type frequency:
numeric	3
________________________
Group variables	None

Variable type: numeric

skim_variable	complete_rate	mean	sd	p0	p25	p50	p75	p100	hist
precio_m2_miles	1	1.28	0.31	0.33	1.08	1.28	1.47	2.33	▁▅▇▃▁
calidad_gral	1	6.02	1.37	1.00	5.00	6.00	7.00	10.00	▁▂▇▅▁
area_hab_m2	1	140.47	47.66	31.03	103.15	137.17	166.48	400.97	▃▇▂▁▁

Y algunas gráficas:

library(patchwork)
g_1 <- ggplot(entrena_casas,
              aes(x = calidad_gral)) + geom_bar()
g_2 <- ggplot(entrena_casas |> 
                filter(calidad_gral <= 9 & calidad_gral > 2),
  aes(x = area_hab_m2, y = precio_m2_miles, 
      colour = calidad_gral, group = calidad_gral)) +
  geom_point(alpha = 0.9) + 
  scale_x_log10() +
  scale_color_gradient(low = "purple", high = "yellow") 
g_1+g_2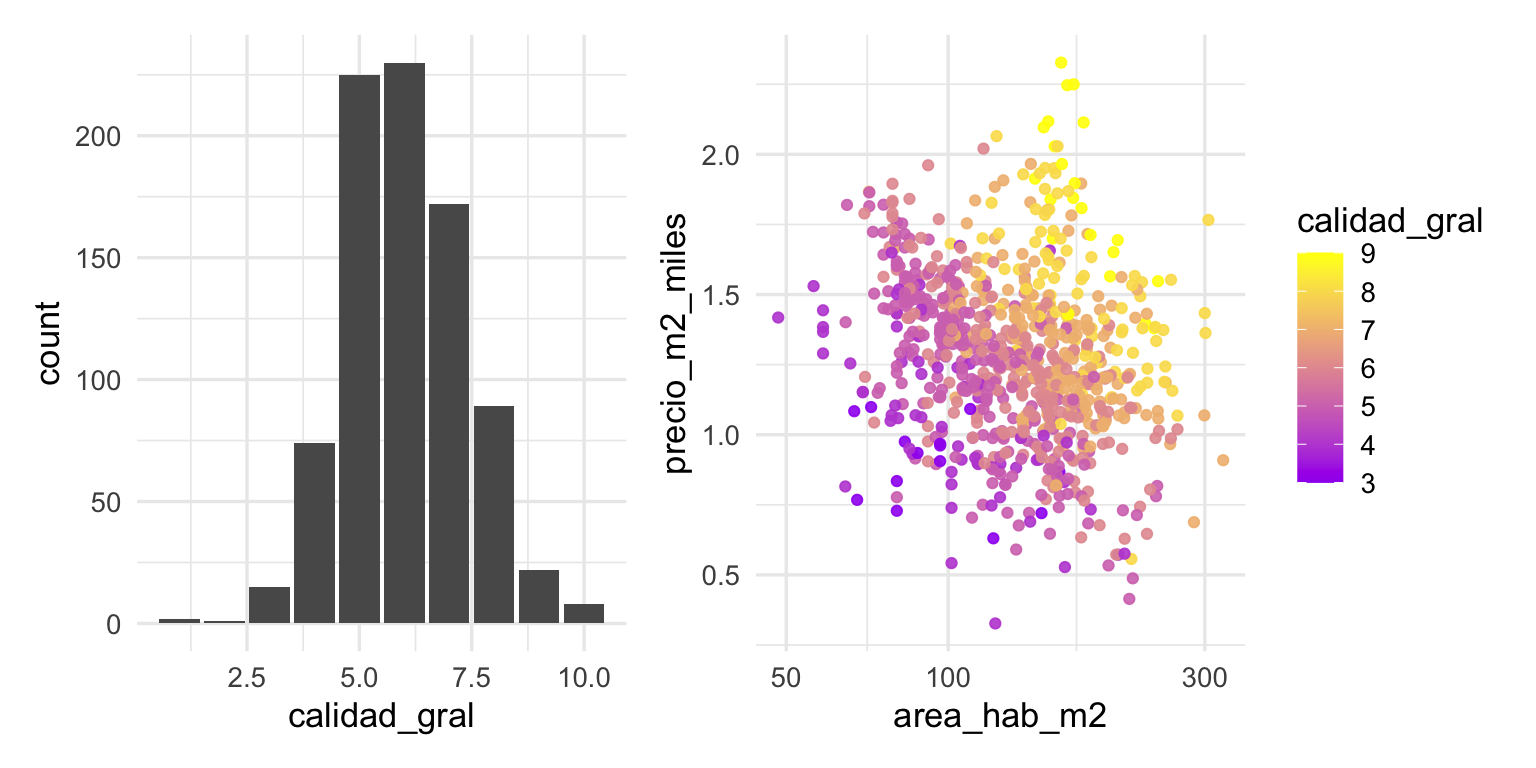

Preprocesamiento

Decidimos hacer entonces la siguiente receta preprocesamiento:

preproceso <- 
  recipe(precio_m2_miles ~ calidad_gral + area_hab_m2, 
         data = entrena_casas) |>
  step_cut(calidad_gral, breaks = c(3, 4, 5, 6, 7, 8, 9)) |> 
  step_log(area_hab_m2) |> 
  step_center(area_hab_m2)

Donde convertimos calidad general en categórica, agrupando los niveles 1,2,3 por un lado, y 9 y 10 por otro. Adicionalmente, obtenemos el logaritmo de area y después la centramos.

preproceso

## Recipe
## 
## Inputs:
## 
##       role #variables
##    outcome          1
##  predictor          2
## 
## Operations:
## 
## Cut numeric for calidad_gral
## Log transformation on area_hab_m2
## Centering for area_hab_m2

Esta receta también la entrenaremos con los datos de entrenamiento.

Definición de modelo

En nuestro caso, simplemente usaremos un modelo lineal

modelo_lineal <- linear_reg()
modelo_lineal

## Linear Regression Model Specification (regression)
## 
## Computational engine: lm

Construir el flujo y entrenamiento

Generalmente, tenemos que entrenar tanto el preprocesamiento como los modelos que queremos ajustar. Es conveniente entonces crear un objeto que junta las dos cosas, un workflow:

flujo_casas <- workflow() |> 
  add_recipe(preproceso) |> 
  add_model(modelo_lineal)

Y ahora entrenamos: se calcula todo lo necesario para hacer el preproceso, y se ajusta por mínimos cuadrados un modelo a las variables que salen del preproceso:

flujo_ajustado <- fit(flujo_casas, data = entrena_casas)
flujo_ajustado

## ══ Workflow [trained] ══════════════════════════════════════════════════════════
## Preprocessor: Recipe
## Model: linear_reg()
## 
## ── Preprocessor ────────────────────────────────────────────────────────────────
## 3 Recipe Steps
## 
## • step_cut()
## • step_log()
## • step_center()
## 
## ── Model ───────────────────────────────────────────────────────────────────────
## 
## Call:
## stats::lm(formula = ..y ~ ., data = data)
## 
## Coefficients:
##        (Intercept)   calidad_gral(3,4]   calidad_gral(4,5]   calidad_gral(5,6]  
##             0.6586              0.2621              0.4628              0.5805  
##  calidad_gral(6,7]   calidad_gral(7,8]   calidad_gral(8,9]  calidad_gral(9,10]  
##             0.7726              1.0167              1.3657              1.5059  
##        area_hab_m2  
##            -0.6246

Métricas y evaluación de desempeño

Hasta este punto, podemos regresar a hacer ajustes en el preproceso y modelo si creemos que es necesario. Una vez que tomamos una decisión final, construimos las predicciones, y evaluamos desempeño.

Primero usamos el flujo ajustado, lo cual preprocesa (con un preprocesador ya fijo) y construye las predicciones (con un modelo fijo ya ajustado):

prueba_casas <- testing(casas_particion)
preds_prueba <- predict(flujo_ajustado, prueba_casas) |> 
  bind_cols(prueba_casas |> select(precio_m2_miles))
head(preds_prueba)

## # A tibble: 6 × 2
##   .pred precio_m2_miles
##   <dbl>           <dbl>
## 1  1.32            1.31
## 2  1.30            1.18
## 3  1.53            1.38
## 4  1.31            1.56
## 5  1.41            1.61
## 6  1.22            1.31

mis_metricas <- metric_set(mape, rmse)
mis_metricas(preds_prueba, truth = precio_m2_miles, estimate = .pred)

## # A tibble: 2 × 3
##   .metric .estimator .estimate
##   <chr>   <chr>          <dbl>
## 1 mape    standard      14.4  
## 2 rmse    standard       0.216

Adicionalmente, graficamos:

ggplot(preds_prueba, aes(x = .pred, y = precio_m2_miles)) +
  geom_point() + geom_abline()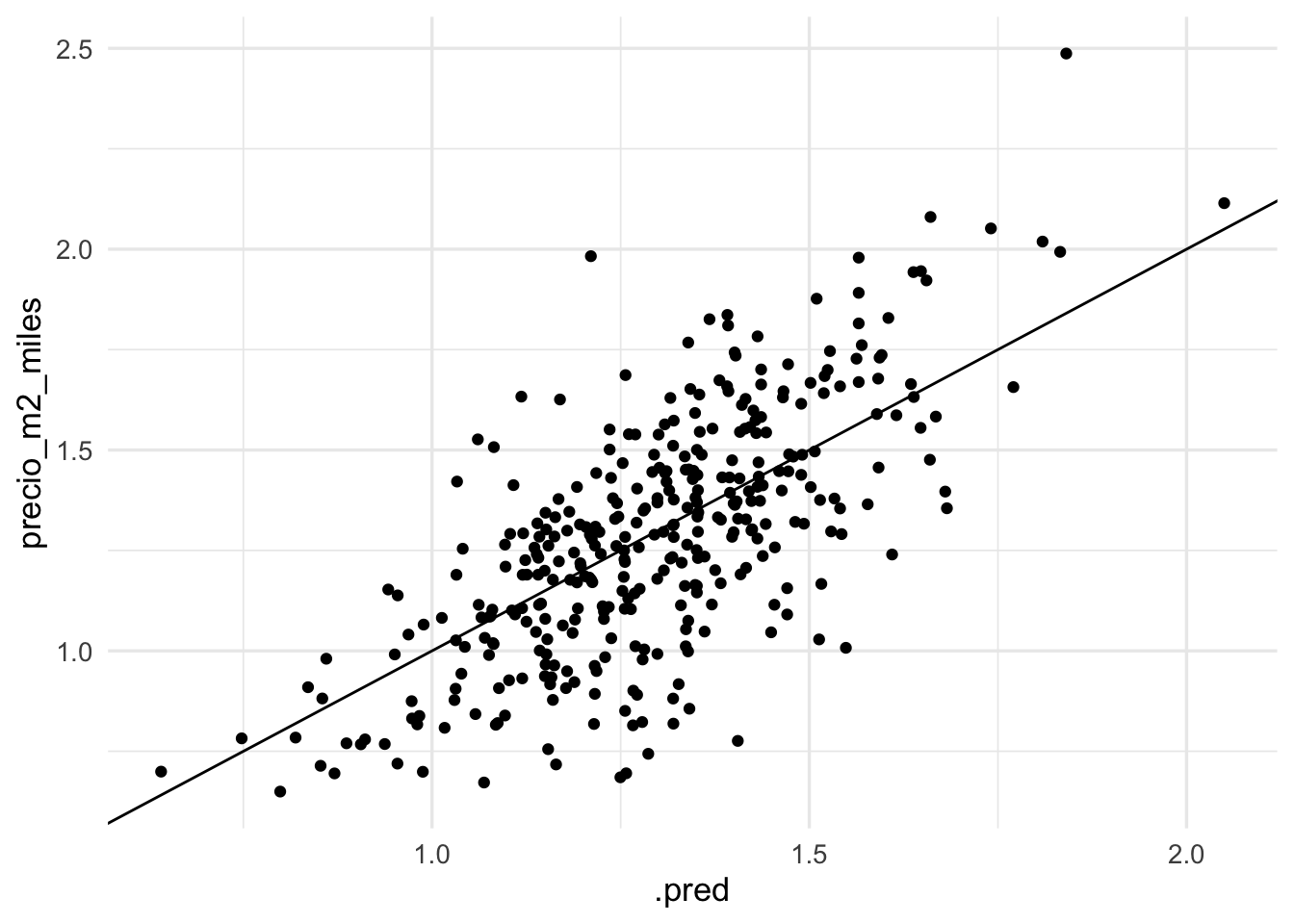

Con esto terminamos el ciclo básico de construcción y validación de modelos predictivos.

3.6 Precisión en la estimación del error

Ahora hacemos algunos cálculos que usamos para decidir el tamaño de la muestra de prueba. Como en cualquier estudio de muestreo, para hacer resto informadamente necesitamos tener algunos conocimientos previos para tener una idea de qué tamaño va a ser el error. En nuestro caso, suponemos que sabemos que en la región que nos interesa los precios por metro cuadrado están generalmente entre 0.5 y 5 mil dólares. Sabemos que una componente grande de este precio va a estar relacionado con la calidad de los acabados, así que en el peor de los casos consideramos que los errores serán de +/- 1 mil dólares. De aquí hacemos un cálculo clásico de tamaño de muestra, donde ponemos \(\sigma = 1\), de modo que si \(m\) es el tamaño de muestra de prueba, entonces el error de estimación del error promedio será de \(2\sigma /\sqrt{m}\). Si ponemos \(m=400\) por ejemplo, entonces

ee <- 2 / sqrt(400)
ee

## [1] 0.1

y el error estándar sería de alrededor de 100 dólares. Consideramos que este nivel de precisión para la estimación del error es suficiente para decidir qué tan útil es nuestro modelo. Nótese ahora que

p_ent <- 0.7
n_prueba <- nrow(casas)*(1-p_ent)
n_prueba

## [1] 359.4

Y entonces escogemos 0.7 de la muestra para entrenar. Dividimos al azar la muestra (en este caso, estamos suponiendo que las predicciones que queremos hacer son para otras casas extraídas de la misma población de casas que cubre nuestra muestra).

En nuestro caso, una vez que hemos “destapado” la muestra de prueba, podemos hacer por ejemplo bootstrap para evaluar la precisión de estimación del error. Es un problema de inferencia usual.

library(infer)
preds_prueba |>
  generate(reps = 1000, type = "bootstrap", variables = .pred) |> 
  group_by(replicate) |> 
  rmse(truth = precio_m2_miles, estimate = .pred) |> 
  select(replicate, stat = .estimate) |>
  get_ci(level = 0.90) |> 
  gt() |> fmt_number(where(is_double), decimals = 3)

## Warning: The `variables` argument is only relevant for the "permute" generation
## type and will be ignored.

lower_ci	upper_ci
0.203	0.230

En este caso, el error de estimación está alrededor de 150 dólares.

3.7 Ejemplo: vecinos más cercanos

Para repasar, probaremos ahora nuestro flujo con otro método simple de predicción: \(k\)-vecinos más cercanos. Supongamos que tenemos la entrada \(\mathbf{x}\) y queremos hacer la predicción de \(y\). Entonces encontramos las \(k\) entradas de entrenamiento más cercanas a \(\mathbf{x}\), y nuestra predicción es el promedio de esas entradas:

\[\hat{f}(\mathbf{x}) = \frac{1}{k}\sum_{x^{(i)}\in N_k(\mathbf{x})} y^{(i)}\] Es decir, buscamos los \(k\) puntos más similares a \(\mathbf{x}\) y promediamos las \(y\) correspondientes.

En este caso, nuestro preproceso será diferente. En primer lugar, podemos usar la variable calidad_gral como numérica. En segundo lugar, es razonable normalizar las dos variables (calidad y área) para que tengan la misma escala (centrando y dividiendo por la desviación estándar):

preproceso_kvmc <- 
  recipe(precio_m2_miles ~ calidad_gral + area_hab_m2, 
         data = entrena_casas) |>
  step_log(area_hab_m2) |> 
  step_normalize(all_numeric_predictors())

Nuestro modelo ahora es (por el momento usaremos simplemente 10 vecinos más cercanos)

modelo_vmc <- nearest_neighbor(neighbors = 10, weight_func = "rectangular") |>
  set_mode("regression") |> 
  set_engine("kknn")
modelo_vmc

## K-Nearest Neighbor Model Specification (regression)
## 
## Main Arguments:
##   neighbors = 10
##   weight_func = rectangular
## 
## Computational engine: kknn

Nuestro flujo es

flujo_casas <- workflow() |> 
  add_recipe(preproceso_kvmc) |> 
  add_model(modelo_vmc)

Ajustamos:

flujo_ajustado_kvmc <- fit(flujo_casas, data = entrena_casas)
flujo_ajustado_kvmc

## ══ Workflow [trained] ══════════════════════════════════════════════════════════
## Preprocessor: Recipe
## Model: nearest_neighbor()
## 
## ── Preprocessor ────────────────────────────────────────────────────────────────
## 2 Recipe Steps
## 
## • step_log()
## • step_normalize()
## 
## ── Model ───────────────────────────────────────────────────────────────────────
## 
## Call:
## kknn::train.kknn(formula = ..y ~ ., data = data, ks = min_rows(10,     data, 5), kernel = ~"rectangular")
## 
## Type of response variable: continuous
## minimal mean absolute error: 0.1613886
## Minimal mean squared error: 0.04383383
## Best kernel: rectangular
## Best k: 10

Y evaluamos:

prueba_casas <- testing(casas_particion)
preds_prueba <- predict(flujo_ajustado_kvmc, prueba_casas) |> 
  bind_cols(prueba_casas |> select(precio_m2_miles))
mis_metricas <- metric_set(mape, rmse)
mis_metricas(preds_prueba, truth = precio_m2_miles, estimate = .pred)

## # A tibble: 2 × 3
##   .metric .estimator .estimate
##   <chr>   <chr>          <dbl>
## 1 mape    standard      14.8  
## 2 rmse    standard       0.226

ggplot(preds_prueba, aes(x = .pred, y = precio_m2_miles)) +
  geom_point() + geom_abline()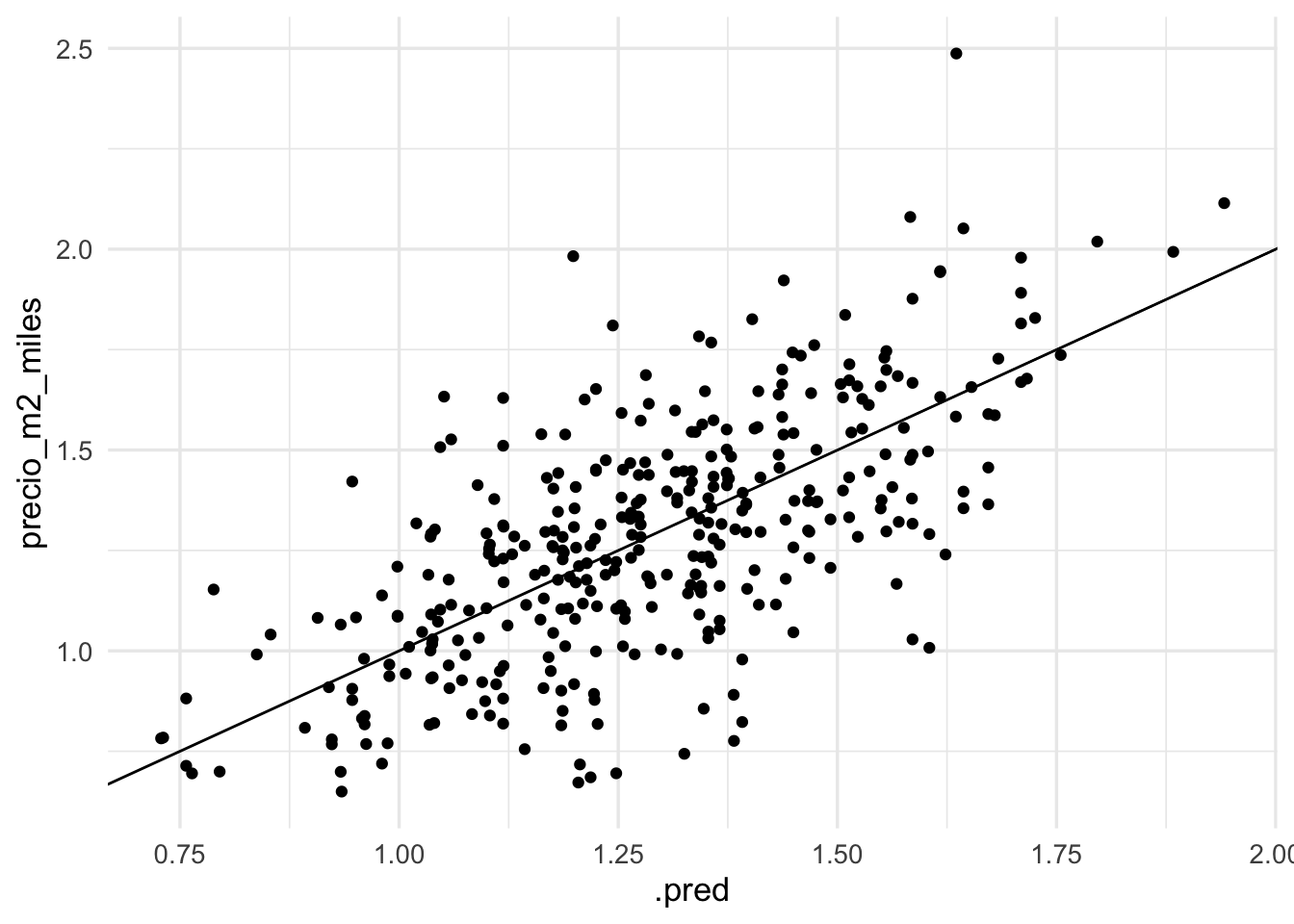

En este caso de dimensión baja, donde no hicimos mucho trabajo de preprocesamiento, el desempeño es similar al de regresión (nota la precisión que obtuvimos en la estimación del error en regresión).

3.8 El problema predictivo en contexto

Los elementos que hemos mostrado arriba proveen los fundamentos para el flujo de trabajo en machine learning. Sin embargo, debemos tomar en cuenta que hay elementos adicionales que hay que tomar en cuenta al decidir si un modelo es suficientemente preciso para algún propósito, o tomar decisiones para problemas de negocios, política pública, etc. Todos estos problemas tienen un contexto que no se puede ignorar.

En primer lugar, este contexto tienen qué ver con los costos y beneficios particulares de los errores en los que incurrimos al tomar decisiones basadas en modelos. Estos costos son a veces difíciles de elicitar y cuantificar con precisión, pero en el análisis deben tomarse en cuenta de alguna forma.

Supongamos por ejemplo que tenemos un plan o tratamiento para aumentar las compras de clientes de una tienda en línea. Es un tratamiento relativamente costoso que no quisiéramos aplicar a todos los clientes, sino que quisiéramos focalizarlo a aquellos clientes que tienen riesgo de tener muy pocas compras, lo cual degrada su valor en nuestra cartera. Por ejemplo, podríamos tener que:

El tratamiento de retención cuesta 500 pesos por cliente,
Estimamos mediante pruebas que nuestro tratamiento aumenta en 2000 pesos de un cliente que gasta menos de 700 pesos, pero no aumenta las ventas si gasta más de 700 pesos.

Una pieza de este problema es entonces un modelo predictivo de las compras de un cliente para el próximo mes en términos de su comportamiento pasado. Tenemos entonces un modelo predictivo \(\hat{f}(x)\) para las compras del próximo mes de cada cliente. Este modelo tiene un error promedio de 25%. En primer lugar, después de aplicar nuestro modelo y obtener las predicciones obtenemos:

clientes <- tibble(id = 1:6000) %>% 
    mutate(pred = 5000*rbeta(length(id), 2, 3))

La pregunta es ¿a qué clientes nos conviene tratar? Pensemos que queremos poner un punto de corte para las predicciones, de forma que si la predicción es más baja que cierto punto de corte, entonces aplicamos el tratamiento.

Tenemos que hacer un análisis costo-beneficio. Primero calculamos los costos:

calc_costos <- function(corte, mejora, corte_trata, costo_trata){
    # compras de los que recibieron tratamiento
    compras_tratados <- filter(clientes, pred < corte) %>% 
        mutate(compras_sim = pred * (1 + rnorm(n(), 0, 0.25))) %>%
        mutate(compras_trata = ifelse(compras_sim < corte_trata, compras_sim + mejora, compras_sim)) %>% 
        summarise(total = sum(compras_trata), total_cf = sum(compras_sim))
    compras_trata <- pull(compras_tratados, total)
    compras_cf <- pull(compras_tratados, total_cf)
    # compras de los que no recibieron tratamiento
    compras_no_tratados <- filter(clientes, pred > corte) %>% 
        mutate(compras = pred * (1 + rnorm(n(), 0, 0.25))) %>%
        summarise(total = sum(compras)) %>% 
        pull(total)
    total <- compras_trata -  costo_trata*nrow(filter(clientes, pred < corte)) - compras_cf 
    total
}
perdidas_sim <- map_dfr(rep(seq(0 , 3000, 100), 100), 
    function(x){
      compras_sim <- calc_costos(x, mejora = 2500, corte_trata = 700, costo_trata = 500)
      tibble(compras = compras_sim, corte = x)
    }) %>% bind_rows

ggplot(perdidas_sim, aes(x = corte, y = compras / 1000)) +
  geom_jitter(width = 10, alpha = 0.2) +
  ylab("Compras (miles)") + xlab("Corte de tratamiento")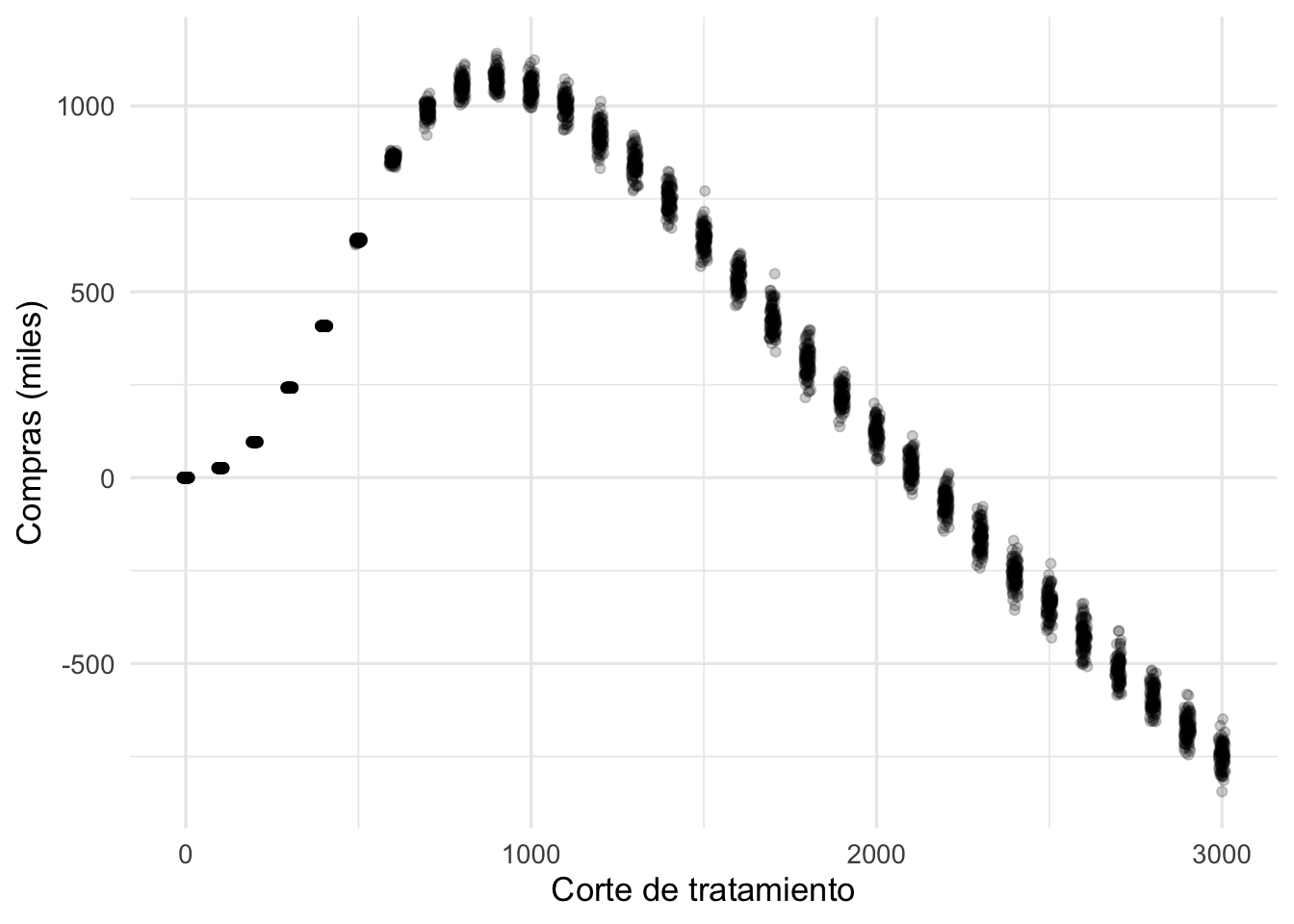

¿Qué acción convedría tomar en este caso? ¿Puedes explicar la forma de esta curva?

Los modelos que utilizamos generalmente son un insumo para tomar una decisión. Aunque usando técnicas estándar y medidas de error usuales podemos construir modelos apropiados, no son suficientes para tomar esa decisión, cuyo contexto más amplio de costo-beneficio debe ser considerado.

Una razón también a favor de usar medidas de error estándar es que

Como analistas o científicos de datos, muchas veces no tenemos completo el contexto de la decisión (especialmente en etapas tempranas de nuestro proyecto), y debemos proveer de guías o herramientas para tomar esa decisión en la que intervienen más actores.
En nuestro entrenamiento como científicos de datos nos concentramos en una cuantas métricas que entendemos mejor, y que están o son fácilmente implementadas universalmente. Por tanto es conveniente dejar para análisis posterior ad-hoc el análisis costo-beneficio particular del problema que nos interesa.

Ejemplo: Los modelos que asignan números a casas en street view de google son modelos estándar de procesamiento de imágenes. Sin embargo, la decisión de marcar o no en el mapa un número requiere consideraciones especiales: por ejemplo, si existe algo de ambigüedad, la decisión se inclina por no asignar números. El nivel de tolerancia se evalúa considerando las consecuencias de etiquetar un lugar con un número equivocado.

2 Introducción

4 Sobreajuste y subajuste