5 Metodos locales y estructura en modelos

5.1 Vecinos más cercanos

Una de las estrategias más simples para hacer predicciones es buscar en nuestro conjunto de entrenamiento casos similares a los que queremos hacer predicciones, y construir predicciones usando esos casos similares.

Por ejemplo, en el método de \(k\) vecinos más cercanos, sea \(\mathbf{x} = (\mathbf{x}_1, \mathbf{x}_2, \ldots, \mathbf{x}_n)\) el caso para el que queremos hacer predicciones. Calculamos para nuestros casos de entrenamiento \((x^{(i)}, y^{(i)})\) la distancia \[d_i = dist(\mathbf{x}, x^{(i)})\] y encontramos los \(k\) casos de entrenamiento don \(d_i\) más chica. Supongamos que \(N(\mathbf{x})\) representa el conjunto de estos \(k\) vecinos más cercanos. Nuestra predicción es entonces el promedio de las respuestas de estos \(k\) vecinos:

\[\hat{f}(\mathbf{x}) = \frac{1}{k}\sum_{i\in N(\mathbf{x})} y^{(i)}.\]

La distancia puede ser seleccionada de distintas maneras: por ejemplo, es común normalizar los datos para que tengan la misma escala, y utilizar la distancia euclideana.

También es posible utilizar una ponderación de casos, donde damos más peso a los valores cercanos y menos peso a los valores menos cercanos:

\[\hat{f}(\mathbf{x}) = \frac{\sum_{i\in N(\mathbf{x})} \phi_iy^{(i)}}{\sum_{i\in N(\mathbf{x})} \phi_i}\]

donde por ejemplo \(\phi_i = \phi(||x^{(i)} - \mathbf{x}||).\) A la función \(\phi\) le llamamos kernel para la distancia, y puede tener distintas formas, por ejemplo

• Si \(\phi\) es constante, se trata del kernel rectangular.
• Si usamos \(\phi_i = \phi(d) = e^{-d^2/2}\), se trata del kernel gaussiano.

Revisa esta liga para entender la implementación del paquete (Schliep and Hechenbichler 2016) en R.

Nota: El suavizamiento loess que quizá has utilizado para producir suavizadores en gráficas de ggplot es una variación de estos método de vecinos cercanos ponderados. Una diferencia es que en este suavizamiento, en lugar de dar un número de vecinos cercanos a considerar, usamos una ventana de distancia alrededor de cada punto:

ggplot(mtcars, aes(x = disp, y = mpg)) +
  geom_point() +
  geom_smooth(method = "loess", span = 0.35, se = FALSE,
              method.args = list(degree = 0, family = "gaussian"))

## `geom_smooth()` using formula 'y ~ x'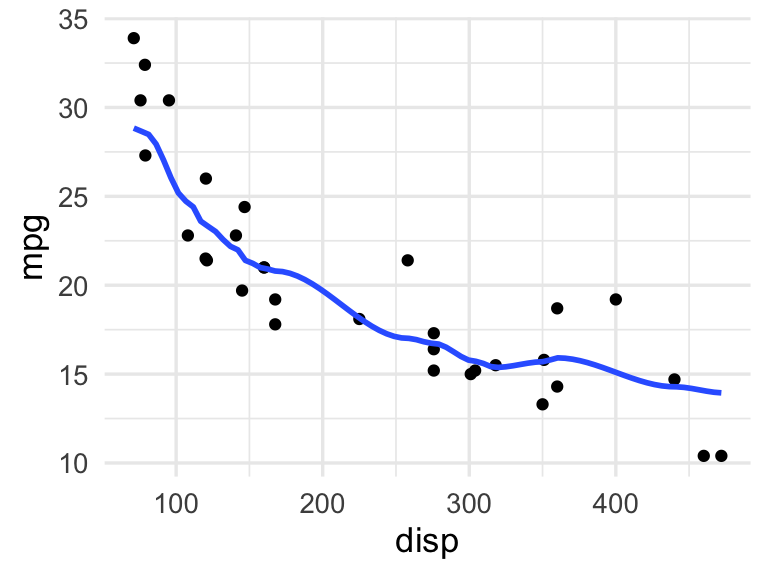

# cuando usamos degree = 1 o degree = 2, el proceso de ponderación
# también incorpora una regresión local

5.2 Ejemplo: precios de casas

Resolveremos el ejemplo de predicción de precios de ventas de casas.

set.seed(68821)
library(tidyverse)
source("R/casas_traducir_geo.R")
casas_split <- initial_split(casas, prop = 0.75)
casas_entrena <- training(casas_split)

receta_casas <- 
  recipe(precio_miles ~ area_hab_m2 + 
           area_garage_m2 + 
           area_sotano_m2 +
           area_lote_m2 +
           calidad_gral + 
           aire_acondicionado +
           año_construccion +
           condicion_venta, 
         data = casas_entrena) |> 
  step_filter(condicion_venta == "Normal") |> 
  step_select(-condicion_venta, skip = TRUE) |> 
  step_normalize(all_numeric_predictors()) |> 
  step_dummy(aire_acondicionado)

• Obsérvese el paso de normalización en la receta. Esto es importante pues consideramos variables en distintas escalas (por ejemplo, año de construcción, tamaños de garage y de áreas habitables, etc.)
• Esta receta es necesaria aprenderla o entrenarla también (¿con qué media se centran las variables por ejemplo?)
• Al incorporarla más adelante en un flujo que incluye el ajuste del modelo podemos hacer el ajuste completo de preprocesamiento y modelo

Un error común, por ejemplo, es centrar con todos los datos disponibles antes de centrar, o usar los datos de prueba para incorporar en la normalización. Explica por qué esto viola los principios de la tarea predictiva fundamental.

Definimos el tipo de modelo que queremos ajustar

casas_modelo <- nearest_neighbor(neighbors = 10, weight_func = "gaussian") |> 
  set_engine("kknn")

workflow_casas <- workflow() |> 
  add_recipe(receta_casas) |> 
  add_model(casas_modelo)

Ajustamos el flujo

ajuste <- fit(workflow_casas, casas_entrena)
ajuste

## ══ Workflow [trained] ══════════════════════════════════════════════════════════
## Preprocessor: Recipe
## Model: nearest_neighbor()
## 
## ── Preprocessor ────────────────────────────────────────────────────────────────
## 4 Recipe Steps
## 
## • step_filter()
## • step_select()
## • step_normalize()
## • step_dummy()
## 
## ── Model ───────────────────────────────────────────────────────────────────────
## 
## Call:
## kknn::train.kknn(formula = ..y ~ ., data = data, ks = min_rows(10,     data, 5), kernel = ~"gaussian")
## 
## Type of response variable: continuous
## minimal mean absolute error: 18.62947
## Minimal mean squared error: 841.5916
## Best kernel: gaussian
## Best k: 10

Y ahora podemos hacer predicciones:

set.seed(8)
casas_prueba <- testing(casas_split) 
ejemplos <- casas_prueba |> sample_n(5)
predict(ajuste, ejemplos) |> 
  bind_cols(ejemplos |> select(precio_miles, area_hab_m2)) |> 
  arrange(desc(precio_miles))

## # A tibble: 5 × 3
##   .pred precio_miles area_hab_m2
##   <dbl>        <dbl>       <dbl>
## 1  256.         275        153. 
## 2  208.         181        156. 
## 3  168.         176.       132. 
## 4  130.         133        118. 
## 5  127.         128.        90.2

Y finalmente podemos evaluar nuestro modelo. En este caso usamos el error promedio porcentual:

metricas <- metric_set(mape, mae, rmse)
metricas(casas_prueba |> bind_cols(predict(ajuste, casas_prueba)), 
     truth = precio_miles, estimate = .pred)

## # A tibble: 3 × 3
##   .metric .estimator .estimate
##   <chr>   <chr>          <dbl>
## 1 mape    standard        11.0
## 2 mae     standard        19.2
## 3 rmse    standard        30.9

ggplot(casas_prueba |> bind_cols(predict(ajuste, casas_prueba)),
       aes(x = .pred, y = precio_miles, colour = condicion_venta)) +
  geom_point() +
  geom_abline(colour = "red") +
  facet_wrap(~condicion_venta)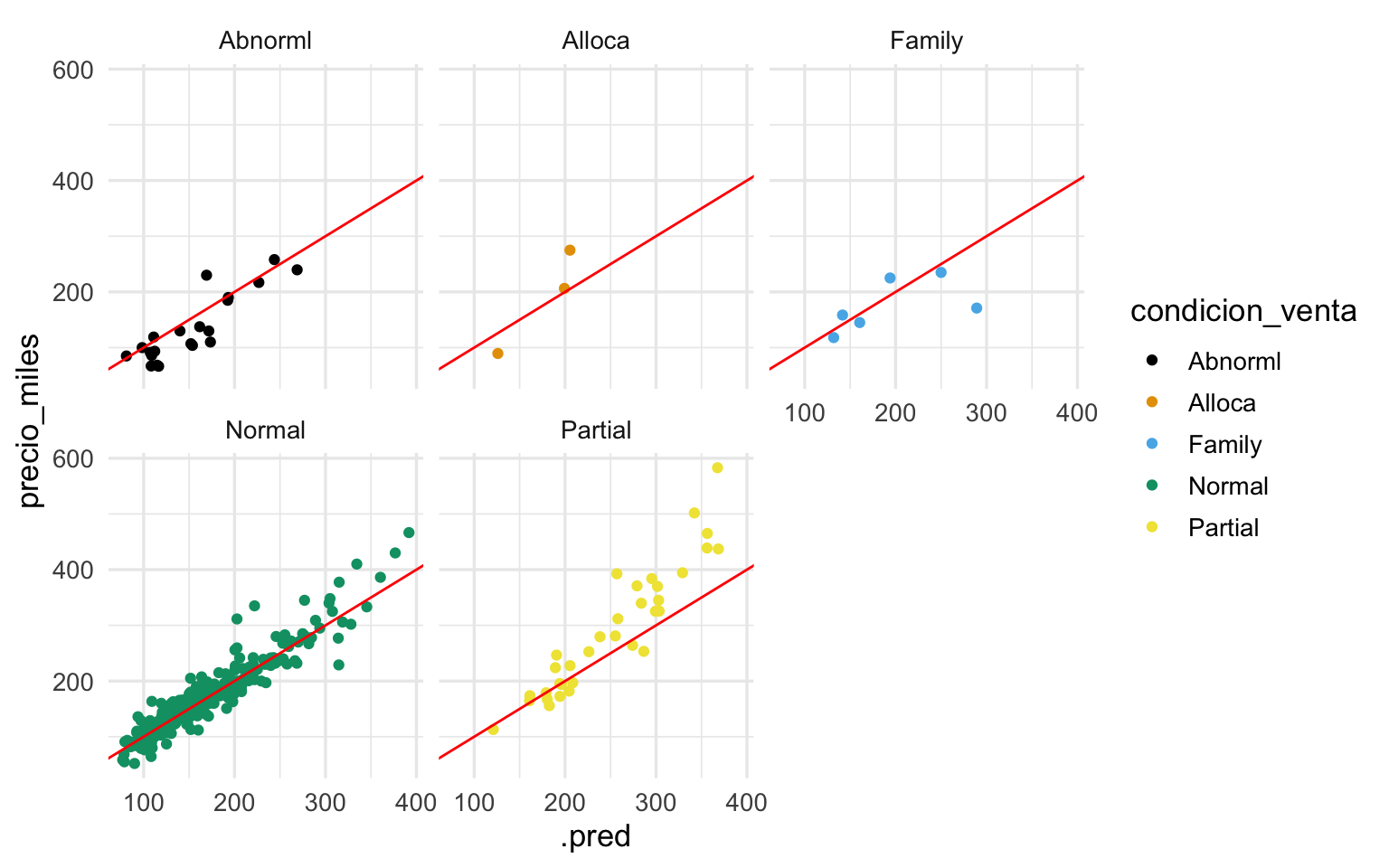

Ejercicio: prueba con distinto número de vecinos más cercanos como hicimos en el ejemplo de datos simulados.

• Los métodos locales son usualmente fácil de explicar e implementar (aunque hacer búsquedas de vecinos cercanos en una base grande puede no ser muy rápido).
• Los métodos locales parecen tener muy pocos supuestos, y parece que pueden adaptarse a cualquier situación. Aparentan ser métodos “universales” en este sentido.
• Sin embargo, veremos por qué para problemas reales no funcionan muy bien: en problemas reales tenemos más de unas cuantas variables, y en ese caso los métodos locales pueden tener fallas graves.

5.3 Dimensión alta

Consideramos el siguiente ejemplo de (Hastie, Tibshirani, and Friedman 2017) de un problema de predicción determinístico:

Consideremos que la salida Y es determinística \(Y = e^{-8\sum_{j=1}^p x_j^2}\). Vamos a usar 1-vecino más cercano para hacer predicciones, con una muestra de entrenamiento de 1000 casos. Generamos \(x^{i}\)’s uniformes en \([1,1]\), para \(p = 2\), y calculamos la respuesta \(Y\) para cada caso:

fun_exp <- function(x) exp(-8 * sum(x ^ 2))
x <- map(1:1000, ~ runif(2, -1, 1))
dat <- tibble(x = x) |> 
        mutate(y = map_dbl(x, fun_exp))
ggplot(dat |> mutate(x_1 = map_dbl(x, 1), x_2 = map_dbl(x, 2)), 
       aes(x = x_1, y = x_2, colour = y)) + geom_point()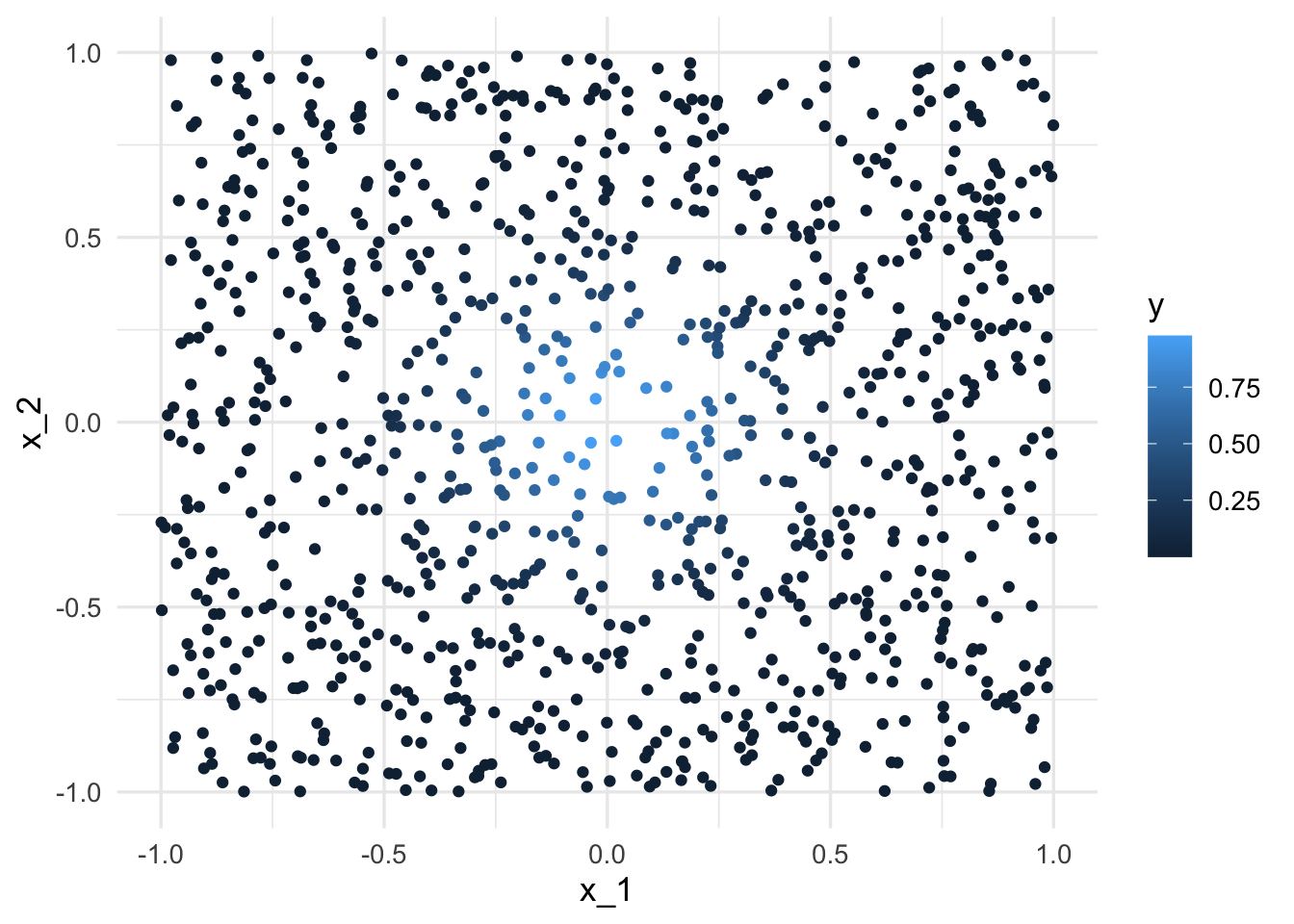

La mejor predicción en \(x_0 = (0,0)\) es \(f((0,0)) = 1\). El vecino más cercano al origen es

dat <- dat |> mutate(dist_origen = map_dbl(x, ~ sqrt(sum(.x^2)))) |> 
  arrange(dist_origen)
mas_cercano <- dat[1, ]
mas_cercano; mas_cercano$x[[1]]

## # A tibble: 1 × 3
##   x             y dist_origen
##   <list>    <dbl>       <dbl>
## 1 <dbl [2]> 0.977      0.0541

## [1]  0.02029541 -0.05016672

Nuestra predicción es entonces \(\hat{f}(0)=\) 0.9768435, que es bastante cercano al valor verdadero (1).

Ahora intentamos hacer lo mismo para dimensión \(p=8\).

x <- map(1:1000, ~ runif(8, -1, 1))
dat <- tibble(x = x) |> 
       mutate(y = map_dbl(x, fun_exp))
dat <- dat |> mutate(dist_origen = map_dbl(x, ~ sqrt(sum(.x^2)))) |> 
  arrange(dist_origen)
mas_cercano <- dat[1, ]
# el vecino más cercano al origen es:
mas_cercano$x[[1]]

## [1]  0.043662590  0.168559216 -0.001719197 -0.297265332 -0.437267008
## [6] -0.118857601 -0.011902106 -0.234526337

Y el resultado es catastrófico. Nuestra predicción puntual es

mas_cercano$y

## [1] 0.04815662

Necesitaríamos una muestra de alrededor de un millón de casos para obtener resultados no tan malos (pruébalo). Si la dimensión es más alta que 8, lo cual no es ninguna situación excepcional en problemas aplicados, entonces para obtener buen desempeño se requieren tamaños de datos que no ocurren en la práctica.

¿Qué es lo que está pasando? La razón es que en dimensiones altas, los puntos de la muestra de entrenamiento están muy lejos unos de otros, y están cerca de la frontera, incluso para tamaños de muestra relativamente grandes como n = 1000. Cuando la dimensión crece, la situación empeora exponencialmente.

La maldición de la dimensionalidad

En dimensiones altas, todos los conjuntos de entrenamiento factibles se distribuyen de manera rala en el espacio de entradas: los puntos de entrenamiento típicamente están lejanos a prácticamente cualquier punto en el que queramos hacer predicciones. El desempeño de los métodos locales no estructurados es mediocre o malo usualmente.

5.4 Métodos lineales y su estructura

¿Cuál es la manera de superar la maldición de la dimensionalidad que mostramos en la sección anterior? ¿Por qué es posible resolver problemas en dimensión alta (imágenes, texto, múltiples características sociodemográficas, etc)? La principal razón

• Muchos datos tienen estructuras o regularidades fuertes, lo que localiza su posición en el espacio de dimensión alta (por ejemplo imágenes).
• Métodos más estructurados que incorporan esas regularidades pueden explotar información que no necesariamente está “cerca” de donde queremos hacer predicciones.

El primer ejemplo de métodos estructurados es la regresión lineal. Si la respuesta que nos interesa modelar tiene una relación aproximadamente lineal con las entradas, entonces requerimos relativamente muy pocos datos para construir predicciones buenas (en el caso extremo, piensa que solo necesitas dos datos para construir una recta: si el problema es de ruido bajo y la relación es lineal, las predicciones de este modelo serán muy buenas).

En regresión lineal, buscamos funciones de predicción de la forma:

\[f(x) = a_0 + a_1 x_1 + a_2 x_2 + \cdots + a_p x_p\] donde \(x_1,\ldots, x_p\) son las entradas. Es quizá la manera más simple de combinar información de estas entradas: la predicción es una suma ponderada de las entradas.

Nótese que antes de hacer predicciones, es necesario entrenar este modelo, que en este caso significa calcular los pesos \(a_i\) apropiados. Una manera simple es encontrar las \(a_i\) que minimizan algún error sobre la muestra de entrenamiento. Por ejemplo, si usamos el error cuadrático, y nuestro conjunto de entrenamiento es \((x^{(1)}, y^{(1)}), (x^{(2)}, y^{(2)}), \ldots, (x^{(N)}, y^{(N)})\), podemos intentar resolver

\[\min_{a_0, a_1, \ldots, a_p}\sum_{i=1}^N (y^{(i)} - f(x^{(i)}))^2\]

que también se puede escribir como

\[\min_{a_0, a_1, \ldots, a_p}\sum_{i=1}^N (y^{(i)} - a_0 - a_1 x^{(i)}_1 - \cdots -a_p x^{(i)}_p)^2.\] Este se llama un problema de mínimos cuadrados, y es posible resolverlo analíticamente (derivando e igualando a cero), o con algún método numérico.

• Nótese que el problema de arriba no intenta “minimizar el error de predicción”. Simplemente intenta ajustar los valores de \(f(x)\) a las \(y\) sobre la mustra de entrenamiento.
• En realidad queremos minimizar el error de predicción, pero este está en términos de la muestra de prueba, que no podemos usarla para entrenar el modelo lineal.
• En consecuencia, este problema de minimización generalmente no es que queremos resolver, y muchas veces lo modificamos para obtener mejor desempeño predictivo: esto lo veremos más adelante.

5.5 Ejemplo: explotando estructura

Este segundo ejemplo también es de (Hastie, Tibshirani, and Friedman 2017). Supongamos que estamos otra vez en un problema de dimensión alta, y ahora intentamos algo similar con una función que es razonable aproximar con una función lineal. Esta función *solo depende de la primera entrada, y las demás componentes de \(x\) son ruido en términos del problema de predicción:

fun_cuad <- function(x)  0.5 * (1 + x[1])^2

Y queremos predecir para \(x=(0,0,\ldots,0)\), cuyo valor exacto es

fun_cuad(0)

## [1] 0.5

Los datos se generan de la siguiente forma:

simular_datos <- function(p = 40){
    x_tbl <- map(1:1000,  ~ tibble(x = runif(p, -1, 1), nombre = paste0("x_", 1:p)))
    dat <- tibble(x_tbl = x_tbl) |> 
      mutate(y = map_dbl(x_tbl, ~ fun_cuad(.x$x)))
    dat |> unnest(cols = c(x_tbl)) |> 
      pivot_wider(names_from = nombre, values_from = x)
}

Por ejemplo, para dimensión \(p=1\) (nótese que una aproximación lineal no es tan mala):

ejemplo <- simular_datos(p = 1) 
ggplot(ejemplo, aes(x = x_1, y = y)) + geom_point() +
    geom_smooth(method = "lm")

## `geom_smooth()` using formula 'y ~ x'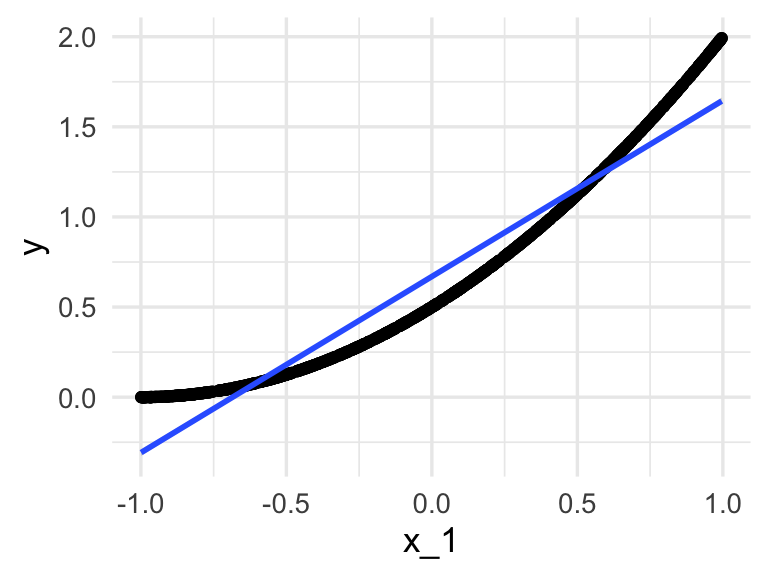

Ahora simulamos el proceso en dimensión \(p=40\): simulamos las entradas, y aplicamos un vecino más cercano

library(tidymodels)

set.seed(831)
dat <- simular_datos(p = 40)
origen <- dat |> select(-y) |> slice(1) |> 
  mutate(across(where(is.numeric), ~ 0))
modelo_vmc <- nearest_neighbor(n = 1) |> 
  set_mode("regression") |> set_engine("kknn")
ajuste_vmc <- modelo_vmc |> fit(y ~ ., dat) 
predict(ajuste_vmc, origen)

## # A tibble: 1 × 1
##   .pred
##   <dbl>
## 1  1.23

Este no es un resultado muy bueno (muy lejos de 0.5). Sin embargo, regresión se desempeña considerablemente mejor:

modelo_lineal <- linear_reg() 
ajuste_lineal <- modelo_lineal |> fit(y ~ ., dat) 
predict(ajuste_lineal, origen)

## # A tibble: 1 × 1
##   .pred
##   <dbl>
## 1 0.666

Donde podemos ver que típicamente la predicción de regresión es mucho mejor que la de 1 vecino más cercano (prueba con otras semillas).

5.6 Ejemplo: precios de casas

Algunas veces, encontrar la estructura apropiada puede requerir más trabajo que simplemente escoger una familia de modelos. En el ejemplo de precios de casas, por ejemplo, podriamos usar:

source("R/casas_traducir_geo.R")
casas_split <- initial_split(casas, prop = 0.75)
casas_entrena <- training(casas_split)
receta_casas <- 
  recipe(precio_miles ~ area_hab_m2 + calidad_gral + 
           area_garage_m2 + area_sotano_m2 + 
           area_lote_m2 + año_construccion + 
           aire_acondicionado + condicion_venta, 
         data = casas_entrena) |> 
  step_filter(condicion_venta == "Normal") |> 
  step_select(-condicion_venta, skip = TRUE) |> 
  step_cut(calidad_gral, breaks = c(3, 5, 7, 8)) |> 
  step_normalize(starts_with("area")) |> 
  #step_discretize(año_construccion, num_breaks = 4) |> 
  step_dummy(calidad_gral, aire_acondicionado) |> 
  step_interact(terms = ~ c(area_hab_m2, area_garage_m2, area_sotano_m2):starts_with("calidad_gral"))

Donde notamos que:

• Cortamos la variable calidad general en niveles
• Construimos variables indicadores de cada rango de calidad general y aire acondicionado para incluir en el modelo lineal
• Agregamos al modelo el producto de las indicadoras de calidad general con las mediciones de metros cuadrados. Esto tiene sentido pues los metros cuadrados tienen distinto valor dependiendo de la calidad de los terminados.

Este proceso de construicción de entradas derivadas de las variable originales se llama ingenería de entradas. Tiene el propósito de utilizar una estructura o especificación apropiada para los datos bajo el modelo que estamos usando (lineal en este caso). Este proceso combina conocimiento de dominio, de los datos, conocimiento de técnicas general de transformaciones y qué tan bien funcionan en distintos casos, e intuición.

Examinamos cómo se ven los datos que vamos a usar para ajustar el modelo:

receta_casas_prep <- prep(receta_casas, verbose = TRUE)

## oper 1 step filter [training] 
## oper 2 step select [training] 
## oper 3 step cut [training] 
## oper 4 step normalize [training] 
## oper 5 step dummy [training] 
## oper 6 step interact [training] 
## The retained training set is ~ 0.17 Mb  in memory.

datos_tbl <- juice(receta_casas_prep)

datos_tbl |>
  mutate(across(where(is.numeric), round, 2)) |> 
  DT::datatable(options = list(scrollX = TRUE))

Y ahora ajustamos nuestro flujo:

flujo_casas <- workflow() |> 
  add_recipe(receta_casas) |> 
  add_model(linear_reg() |> set_engine("lm"))
ajuste <- fit(flujo_casas, casas_entrena)

ajuste |> extract_fit_parsnip() |> broom::tidy() |> 
  mutate(across(where(is.numeric), round, 2)) |> 
  select(term, estimate) |> 
  gt()

term	estimate
(Intercept)	-544.09
area_hab_m2	10.66
area_garage_m2	15.24
area_sotano_m2	9.01
area_lote_m2	8.83
año_construccion	0.34
calidad_gral_X.3.5.	-0.31
calidad_gral_X.5.7.	24.87
calidad_gral_X.7.8.	43.36
calidad_gral_X.8.10.	69.78
aire_acondicionado_Y	19.67
area_hab_m2_x_calidad_gral_X.3.5.	4.98
area_hab_m2_x_calidad_gral_X.5.7.	18.50
area_hab_m2_x_calidad_gral_X.7.8.	27.16
area_hab_m2_x_calidad_gral_X.8.10.	37.81
area_garage_m2_x_calidad_gral_X.3.5.	-10.68
area_garage_m2_x_calidad_gral_X.5.7.	-5.55
area_garage_m2_x_calidad_gral_X.7.8.	1.65
area_garage_m2_x_calidad_gral_X.8.10.	6.08
area_sotano_m2_x_calidad_gral_X.3.5.	-0.89
area_sotano_m2_x_calidad_gral_X.5.7.	2.89
area_sotano_m2_x_calidad_gral_X.7.8.	5.39
area_sotano_m2_x_calidad_gral_X.8.10.	6.13

Nótese que:

• En esta tabla están los coeficientes \(a_i\) en las covariables que creamos a partir de las variables de entrada.
• El modelo lineal no tiene que ser lineal en las variables que recibimos originalmente en la tabla de datos.
• En este ejemplo, convertimos algunas variables a dummy, y multiplicamos algunas variables de área por esas variables dummy.

metricas <- metric_set(mape, mae, rmse)
casas_prueba <- testing(casas_split)
metricas(casas_prueba |> bind_cols(predict(ajuste, casas_prueba)), 
     truth = precio_miles, estimate = .pred)

## # A tibble: 3 × 3
##   .metric .estimator .estimate
##   <chr>   <chr>          <dbl>
## 1 mape    standard        10.9
## 2 mae     standard        19.5
## 3 rmse    standard        29.2

5.7 Ingeniería de entradas

Hay una gran cantidad de transformaciones que podemos considerar para mejorar el desempeño de un modelo. En este caso vimos ejemplos donde:

• Convertimos variables categóricas a variables indicadoras (dummy) para incluirlas en nuestro modelo
• Discretizamos una variable continua para capturar efectos no lineales
• Incluímos interacciones para que los efecto lineal de una variable dependa de otras variables

Pero existen muchas otras que son muy útiles, entre ellas mencionamos:

• Expansión de entradas con splines o polinomios para incluir efectos no lineales sin tener que discretizar.
• Transformaciones como logaritmo y raíz cuadrada que comprimen colas largas de variables de entrada
• Tratamiento de variables categóricas de alta cardinalidad (qué hacer con los niveles que tienen pocos valores?)
• Tratamiento de colecciones de mediciones que se refieren a una unidad (por ejemplo, cada unidad tiene un número variable de observaciones de cierto tipo)

Una buena guía puede consultarse aquí: Feature Engineering and Selection: A Practical Approach for Predictive Models

5.8 Ejemplo: precios de casas

5.9 Regresión ridge: escogiendo el parámetro de complejidad

Intentamos ahora con más preprocesamiento, incluyendo más variables e interacciones:

receta_casas_ext <- 
  recipe(precio_miles ~ calidad_gral +
           area_hab_m2 + 
           area_garage_m2 + area_sotano_m2 + 
           area_2o_piso_m2 +
           area_lote_m2 + 
           año_construccion + año_venta +
           nombre_zona + 
           aire_acondicionado + condicion_venta +
           condicion_gral + condicion_exteriores + tipo_sotano +
           calidad_sotano +
           baños_completos +  
           forma_lote + tipo_edificio + estilo + num_coches +
           año_venta, 
         data = casas_entrena) |> 
  step_filter(condicion_venta == "Normal") |> 
  step_select(-condicion_venta, skip = TRUE) |> 
  step_cut(calidad_gral, breaks = c(3, 5, 7, 8)) |> 
  step_cut(condicion_gral, breaks = c(3, 5, 7, 8)) |> 
  step_mutate(sin_piso_2 = as.numeric(area_2o_piso_m2 == 0)) |> 
  step_unknown(tipo_sotano, calidad_sotano, new_level = "sin sótano") |> 
  step_other(nombre_zona, threshold = 0.02) |>
  step_novel(condicion_exteriores) |> 
  step_ns(año_venta, deg_free = 3) |> 
  step_ns(año_construccion, deg_free = 3) |> 
  step_dummy(calidad_gral, condicion_gral, condicion_exteriores, aire_acondicionado,
        tipo_sotano, forma_lote, tipo_edificio, estilo,
        nombre_zona, calidad_sotano) |> 
  step_interact(terms = ~ c(area_hab_m2, area_garage_m2, 
        area_sotano_m2, area_2o_piso_m2):starts_with("calidad_gral")) |> 
  step_interact(terms = ~ area_sotano_m2:starts_with("calidad_sotano")) |> 
  step_interact(terms = ~ c(area_hab_m2, area_garage_m2, 
        area_sotano_m2, area_2o_piso_m2):starts_with("condicion_gral")) |> 
  step_interact(terms = ~ c(area_hab_m2, area_garage_m2, 
        area_sotano_m2, area_2o_piso_m2):starts_with("nombre_zona")) |> 
  step_nzv(all_numeric_predictors(), freq_cut = 600)

Para ver el número de entradas de este modelo:

prep(receta_casas_ext) |> juice() |> dim()

## [1] 900 144

flujo_casas_ext <- workflow() |> 
  add_recipe(receta_casas_ext) |> 
  add_model(linear_reg() |> set_engine("lm"))
ajuste <- fit(flujo_casas_ext, casas_entrena)

metricas <- metric_set(mape, mae, rmse)
casas_prueba <- testing(casas_split)
metricas(casas_prueba |> bind_cols(predict(ajuste, casas_prueba)), 
     truth = precio_miles, estimate = .pred)

## Warning in predict.lm(object = object$fit, newdata = new_data, type =
## "response"): prediction from a rank-deficient fit may be misleading

## # A tibble: 3 × 3
##   .metric .estimator .estimate
##   <chr>   <chr>          <dbl>
## 1 mape    standard        9.13
## 2 mae     standard       16.7 
## 3 rmse    standard       25.7

Nótese dos cosas: logramos un desempeño considerablemente mejor que nuestros dos modelos anteriores, pero también una advertencia de que nuestra matriz de diseño no es de ranƒgo completo, lo cual suguiere también que es posible que nuestro modelo sufra de algo de sobreajuste. Veremos cómo remediar esta situación en la siguiente sección.

• Hacemos expansión de entradas y transformaciones para reducir el sesgo de nuestro modelo
• Puede ser, sin embargo, que esto nos lleve a problemas de predicciones inestables y con varianza alta. Aunque reducimos el problema de sesgo, ahora nos enfrentamos a problemas de varianza, que con el modelo simple no eran importantes.

En la siguiente sección veremos cómo controlar la varianza.