8 Problemas de clasificación

8.1 El problema de clasificación

Una variable \(g\) categórica o cualitativa toma valores que no son numéricos. Por ejemplo, si \(g\) denota el estado del contrato de celular de un cliente dentro de un año, podríamos tener \(g\in \{ activo, cancelado\}\).

En un problema de clasificación buscamos predecir una variable respuesta categórica \(G\) en función de otras variables de entrada \(x=(x_1,x_2,\ldots, x_p)\).

Ejemplos

Predecir si un cliente cae en impago de una tarjeta de crédito, de forma que podemos tener \(g=corriente\) o \(g=impago\). Variables de entrada podrían ser \(x_1=\) porcentaje de saldo usado, \(x_2=\) atrasos en los úlltimos 3 meses, \(x_3=\) edad, etc
En nuestro ejemplo de reconocimiento de dígitos tenemos \(g\in\{ 0,1,\ldots, 9\}\). Nótese que los dígitos no se pueden considerar como valores numéricos (son etiquetas). Tenemos que las entradas \(x_j\) para \(j=1,2,\ldots, 256\) son valores de cada pixel (imágenes blanco y negro).
En reconocimiento de imágenes quiza tenemos que \(g\) pertenece a un conjunto que típicamente contiene miles de valores (manzana, árbol, pluma, perro, coche, persona, cara, etc.). Las \(x_j\) son valores de pixeles de la imagen para tres canales (rojo, verde y azul). Si las imágenes son de 100x100, tendríamos 30,000 variables de entrada.

8.2 ¿Qué estimar en problemas de clasificación?

En problemas de regresión, consideramos modelos de la forma \(y= f(x) + \epsilon\), y vimos que podíamos plantear el problema de aprendizaje supervisado como uno donde el objetivo es estimar lo mejor que podamos la función \(f\) mediante un estimador \(\hat{f}\). Usamos entonces \(\hat{f}\) para hacer predicciones. En el caso de regresión:

\(f(x)\) es la relación sistemática de \(y\) en función de \(x\)
Dada \(x\), la variable observada \(y = f(x) + \epsilon\) es una variable aleatoria (\(\epsilon\) depende de otras variables que no conocemos).

No podemos usar un modelo así en clasificación pues \(g\) no es numérica. Sin embargo, podemos pensar que \(x\) nos da cierta información probabilística acerca de las clases que pueden ocurrir:

\(P(g|x)\) es la probabilidad condicional de observar \(g\) si tenemos \(x\). Esto es la información sistemática de \(g\) en función de \(x\)
Dada \(x\), la clase observada \(g\) es una variable aleatoria (depende de otras variables que no conocemos). En analogía con el problema de regresión, quisiéramos estimar las probabilidades condicionales \(P(g|x) = p_g (x)\), que es la parte sistemática de la relación de \(g\) en función de \(x\). Normalmente codificamos las clases \(g\) con una etiqueta numérica, de modo que \(g\in\{0,1,\ldots, K-1\}\):

Ejemplo

(Impago de tarjetas de crédito) Supongamos que \(X=\) porcentaje del crédito máximo usado, y \(g\in\{0, 1\}\), donde \(1\) corresponde al corriente y \(0\) representa impago. Podríamos tener, por ejemplo: \[\begin{align*} p_1(10\%) &= P(g=1|x=10\%) = 0.95 \\ p_0(10\%) &= P(g=0|x=10\%) = 0.05 \end{align*}\] y \[\begin{align*} p_1(95\%) &= P(g=1|x=95\%) = 0.70 \\ p_0(95\%) &= P(g=0|x=95\%) = 0.30 \end{align*}\] En resumen:

En problemas de clasificación queremos estimar la parte sistemática de la relación de \(g\) en función \(x\), que en este caso quiere decir que buscamos estimar las probabilidades condicionales: \[\begin{align*} p_0(x) &= P(g=0|x), \\ p_1(x) &= P(g=1|x), \\ \vdots & \\ p_{K-1}(x) &= P(g=K-1|x) \end{align*}\] para cada valor \(x\) de las entradas.

A partir de estas probabilidades de clase podemos producir un clasificador de varias maneras (las discutiremos más adelante). La forma más simple es usando el clasificador de Bayes:

Dadas las probabilidades condicionales \(p_0(x),p_1(x),p_2(x),\ldots, p_{K-1}(x)\), el clasificador de Bayes asociado está dado por \[\hat{g}_{bayes} (x) = \arg\max_{g} p_g(x)\] Es decir, clasificamos en la clase que tiene máxima probabilidad de ocurrir.

Nótese sin embargo que este clasificador colapsa información útil de las probabilidades de clase (por ejemplo, no es lo mismo que \(p_1(x) = 0.55\) vs \(p_1(x) = 0.98\): cada uno de estos casos puede requerir decisiones diferentes).

Ejemplo

(Impago de tarjetas de crédito) Supongamos que \(x=\) porcentaje del crédito máximo usado, y \(g\in\{0, 1\}\), donde \(1\) corresponde al corriente y \(0\) representa impago. Las probabilidades condicionales de clase para la clase al corriente podrían ser, por ejemplo:

\(p_1(x) = P(g=1|x) =0.95\) si \(x < 0.15\)
\(p_1(x) = P(g=1|x) = 0.95 - 0.7(x - 0.15)\) si \(x>=0.15\)

Estas son probabilidades, pues hay otras variables que influyen en que un cliente permanezca al corriente o no en sus pagos más allá de información contenida en el porcentaje de crédito usado. Nótese que estas probabilidades son diferentes a las no condicionadas, por ejempo, podríamos tener que a total \(P(g=1)=0.83\)

p_1 <- function(x){
  ifelse(x < 0.15, 0.95, 0.95 - 0.7 * (x - 0.15))
}
ggplot(tibble(x = seq(0, 1, 0.01)), aes(x = x)) + 
    stat_function(fun = p_1)  +
    ylab("p_1")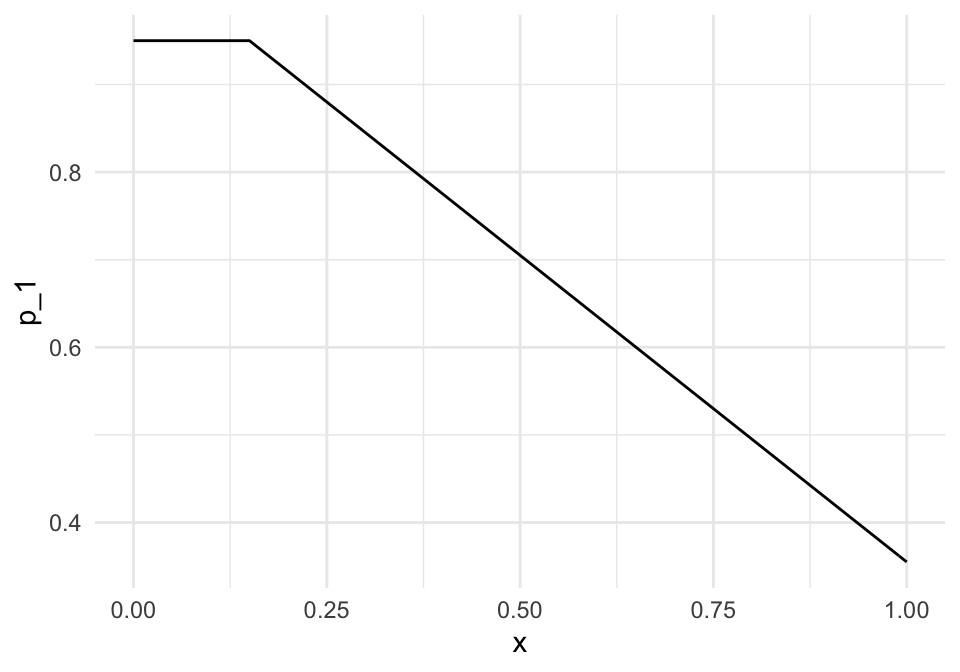

¿Por qué en este ejemplo ya no mostramos la función \(p_0(x)\)?

Si usamos el clasificador de Bayes, tendríamos por ejemplo que si \(x=10\%\), como \(p_1(10\%) = 0.95\) y \(p_0(10\%)=0.05\), nuestra predicción de clase sería \(\hat{g}(10\%) = 1\) (al corriente), pero si \(x=90\%\), \(\hat{g}(90\%) = 0\) (impago), pues \(p_1(90\%) = 0.425\) y \(p_0(90\%) = 0.575\).

8.3 Estimación de probabilidades de clase

¿Cómo estimamos ahora las probabilidades de clase a partir de una muestra de entrenamiento? Veremos por ahora dos métodos: k-vecinos más cercanos y regresión logística.

Ejemplo

Vamos a generar unos datos con el modelo simple del ejemplo anterior:

simular_impago <- function(n = 500){
    # suponemos que los valores de x están concentrados en valores bajos,
    # quizá la manera en que los créditos son otorgados
    x <- pmin(rexp(n, 100 / 40), 1)
    # las probabilidades de estar al corriente:
    probs <- p_1(x)
    # finalmente, simulamos cuáles clientes siguen al corriente y cuales no:
    g <- rbinom(length(x), 1, probs)
    dat_ent <- tibble(x = x, p_1 = probs, g = g)
    dat_ent
}
set.seed(193)
dat_ent  <- simular_impago() |> select(x, g) 
dat_ent |> sample_n(20)

## # A tibble: 20 × 2
##          x     g
##      <dbl> <int>
##  1 0.118       1
##  2 0.109       1
##  3 0.444       1
##  4 0.153       1
##  5 0.100       1
##  6 0.0109      1
##  7 0.216       1
##  8 1           0
##  9 0.0846      1
## 10 0.144       1
## 11 0.377       0
## 12 0.0908      1
## 13 0.128       1
## 14 0.00262     1
## 15 0.411       1
## 16 0.545       1
## 17 0.402       1
## 18 0.0544      1
## 19 0.00265     1
## 20 0.0927      1

Como este problema es de dos clases, podemos graficar como sigue (agregamos variación artificial para evitar traslape de los puntos):

graf_1 <- ggplot(dat_ent, aes(x = x)) +
  geom_jitter(aes(colour = factor(g), y = g), 
    width=0.02, height=0.1) + ylab("") + 
    labs(colour = "Clase")
graf_1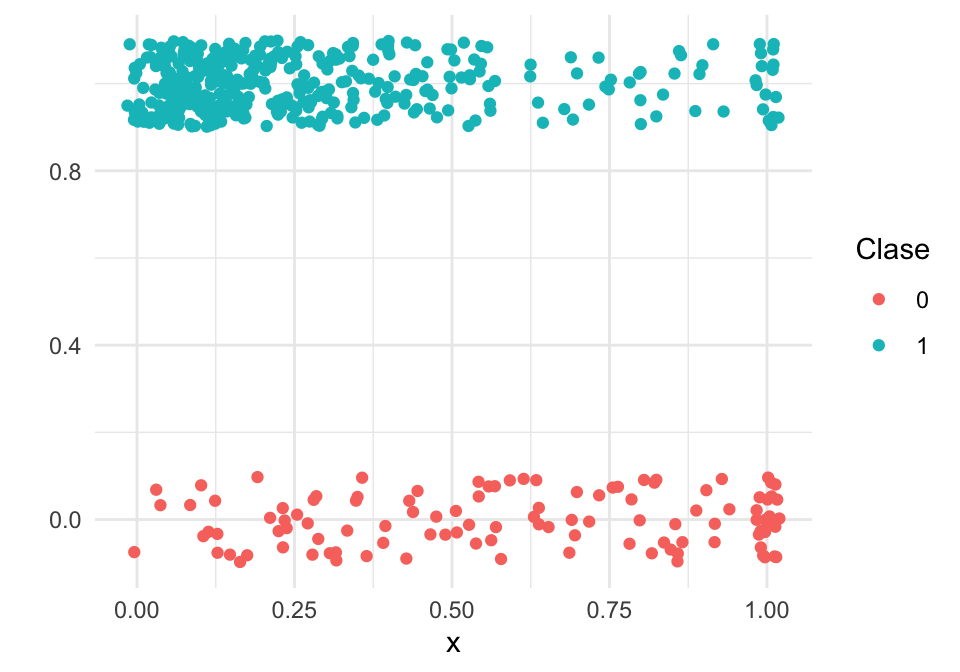

8.4 k-vecinos más cercanos

La idea general de \(k\) vecinos más cercanos es simple: nos fijamos en las tasas locales de impago alrededor de la \(x\) para la que queremos predecir, y usamos esas tasas locales para estimar la probabilidad condicional.

Supongamos entonces que tenemos un conjunto de entrenamiento \[{\mathcal L}=\{ (x^{(1)},g^{(1)}),(x^{(2)},g^{(2)}), \ldots, (x^{(N)}, g^{(N)}) \}\]

La idea es que si queremos predecir en \(x_0\), busquemos varios \(k\) vecinos más cercanos a \(x_0\), y estimamos entonces \(p_g(x)\) como la proporción de casos tipo \(g\) que hay entre los \(k\) vecinos de \(x_0\).

Vemos entonces que este método es un intento de hacer una aproximación directa de las probabilidades condicionales de clase.

Podemos escribir esto como:

k vecinos más cercanos para clasificación Estimamos contando los elementos de cada clase entre los \(k\) vecinos más cercanos: \[\hat{p}_g (x_0) = \frac{1}{k}\sum_{x^{(i)} \in N_k(x_0)} I( g^{(i)} = g),\]

para \(g=1,2,\ldots, K\), donde \(N_k(x_0)\) es el conjunto de \(k\) vecinos más cercanos en \({\mathcal L}\) de \(x_0\), y \(I(g^{(i)}=g)=1\) cuando \(g^{(i)}=g\), y cero en otro caso (indicadora). Usualmente normalizamos las variables de entrada \((X_1, \ldots, X_p)\) antes de calcular las distancias que usamos para encontrar los vecinos, especialmente si estas variables están en distintas escalas.

Ejemplo

Regresamos a nuestro problema de impago. Vamos a intentar estimar la probabilidad condicional de estar al corriente usando k vecinos más cercanos (curva roja):

vmc_modelo <- nearest_neighbor(neighbors = 100, weight_func = "gaussian") |> 
  set_engine("kknn") |> 
  set_mode("classification")
ajuste_vmc <- vmc_modelo |> fit(factor(g, levels = c(1, 0)) ~ x, dat_ent)
# para graficar:
graf_kvmc <- tibble(x = seq(0, 1, 0.01))
graf_kvmc <- predict(ajuste_vmc, graf_kvmc, type = "prob") |> 
  bind_cols(graf_kvmc) |> 
  select(x, .pred_1)
graf_kvmc |> head()

## # A tibble: 6 × 2
##       x .pred_1
##   <dbl>   <dbl>
## 1  0      0.947
## 2  0.01   0.946
## 3  0.02   0.948
## 4  0.03   0.954
## 5  0.04   0.973
## 6  0.05   0.985

# convertir g a factor para usar clasificación
graf_verdadero <- tibble(x = seq(0, 1, 0.01), p_1 = p_1(x))
graf_2 <- graf_1 + 
  geom_line(data = graf_kvmc, aes(y = .pred_1), colour = 'red', size=1.2) +
  geom_line(data = graf_verdadero, aes(y = p_1)) +
  ylab('Probabilidad al corriente') + xlab('% crédito usado') 
graf_2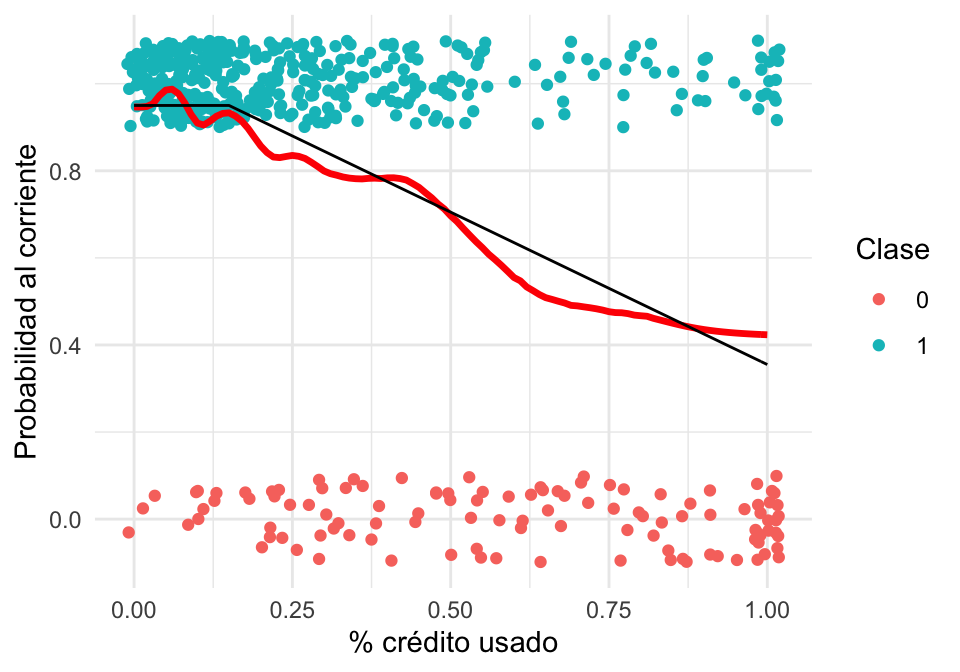

Igual que en el caso de regresión, ahora tenemos qué pensar cómo validar nuestra estimación, pues no vamos a tener la curva negra real para comparar.

Arriba denotamos las probabilidades teóricas como \(p_0 (x), p_1 (x), \ldots, p_{K-1} (x)\). Denotamos probabilidades estimadas como \(\hat{p}_0 (x), \hat{p}_1 (x), \ldots, \hat{p}_{K-1} (x)\)

8.5 Ejemplo: diabetes

Consideremos datos de diabetes en mujeres Pima:

A population of women who were at least 21 years old, of Pima Indian heritage and living near Phoenix, Arizona, was tested for diabetes according to World Health Organization criteria. The data were collected by the US National Institute of Diabetes and Digestive and Kidney Diseases. We used the 532 complete records after dropping the (mainly missing) data on serum insulin.

npreg number of pregnancies.
glu plasma glucose concentration in an oral glucose tolerance test.
bp diastolic blood pressure (mm Hg).
skin triceps skin fold thickness (mm).
bmi body mass index (weight in kg/(height in m)^2).
ped diabetes pedigree function.
age age in years.
type Yes or No, for diabetic according to WHO criteria.

diabetes_ent <- as_tibble(MASS::Pima.tr)
diabetes_pr <- as_tibble(MASS::Pima.te)
diabetes_ent

## # A tibble: 200 × 8
##    npreg   glu    bp  skin   bmi   ped   age type 
##    <int> <int> <int> <int> <dbl> <dbl> <int> <fct>
##  1     5    86    68    28  30.2 0.364    24 No   
##  2     7   195    70    33  25.1 0.163    55 Yes  
##  3     5    77    82    41  35.8 0.156    35 No   
##  4     0   165    76    43  47.9 0.259    26 No   
##  5     0   107    60    25  26.4 0.133    23 No   
##  6     5    97    76    27  35.6 0.378    52 Yes  
##  7     3    83    58    31  34.3 0.336    25 No   
##  8     1   193    50    16  25.9 0.655    24 No   
##  9     3   142    80    15  32.4 0.2      63 No   
## 10     2   128    78    37  43.3 1.22     31 Yes  
## # … with 190 more rows

Intentaremos predecir diabetes dependiendo del BMI:

library(ggplot2)
ggplot(diabetes_ent, aes(x = bmi, y= as.numeric(type=='Yes'), colour = type)) +
  geom_jitter(height = 0.05)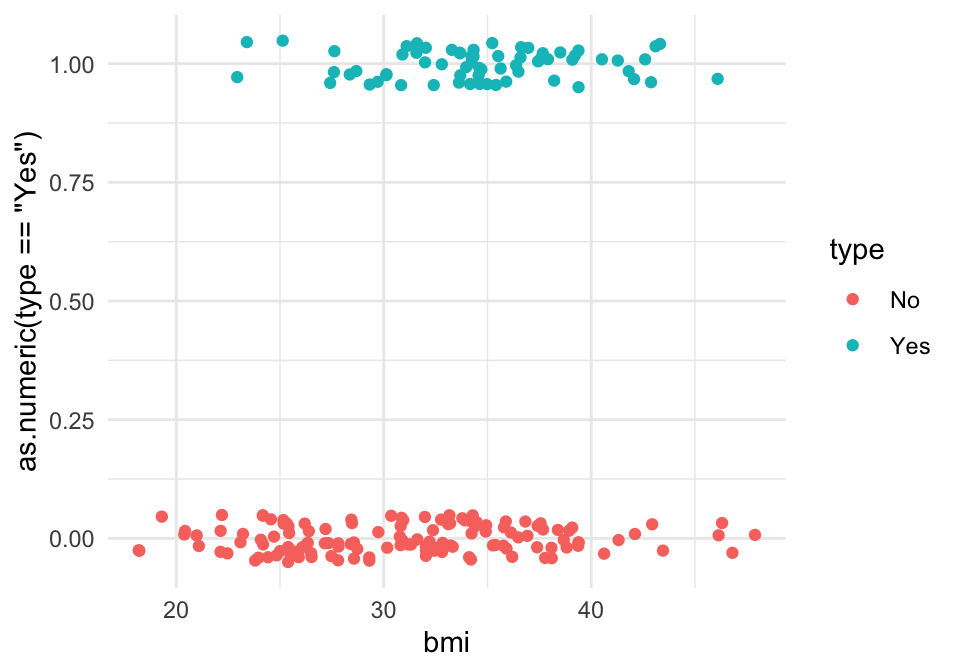

Usamos \(30\) vecinos más cercanos para estimar \(p_g(x)\):

graf_data <- tibble(bmi = seq(20, 45, 1))
# ajustar modelo
ajuste_vmc_diabetes <- vmc_modelo |> set_args(neighbors = 30) |> 
  fit(type ~ bmi, diabetes_ent)
# graficar
graf_data <- predict(ajuste_vmc_diabetes, graf_data, type = "prob") |> 
  bind_cols(graf_data) |> 
  select(bmi, .pred_Yes)
ggplot(diabetes_ent, aes(x = bmi)) + 
  geom_point(aes(y = as.numeric(type == "Yes"), colour = type)) + 
  geom_line(data = graf_data, aes(y = .pred_Yes)) +
  ylab('Probabilidad diabetes')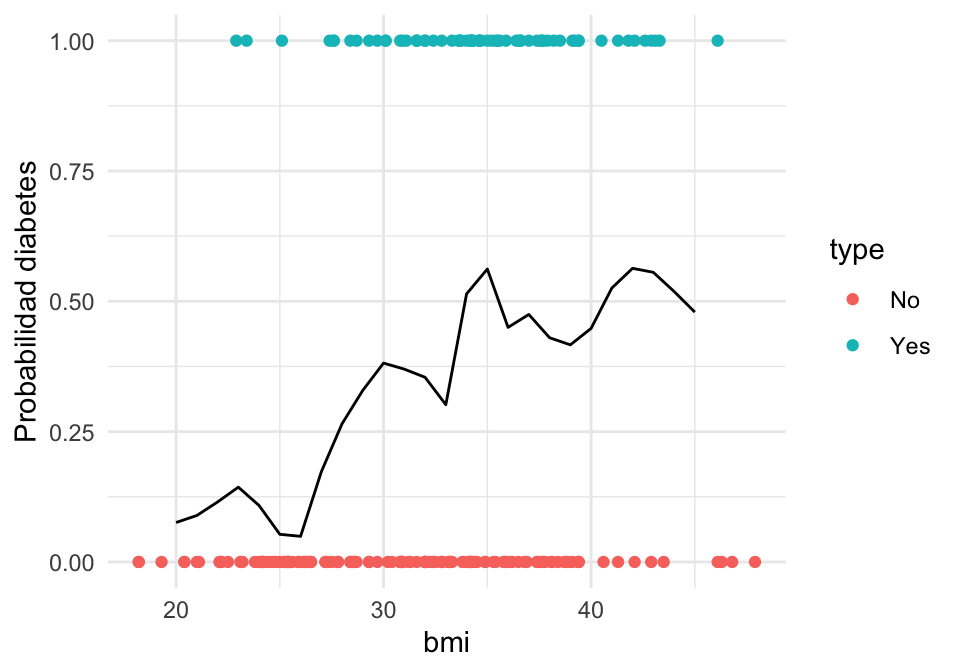

8.6 Error para modelos de clasificación

En regresión, vimos que la pérdida cuadrática era una opción razonable para ajustar modelos, y también para evaluar su desempeño. Ahora necesitamos una pérdida apropiada para trabajar con modelos de clasificación.

Consideremos entonces que tenemos una estimación \(\hat{p}_g(x)\) de las probabilidad de clase. Supongamos que observamos ahora \((x, g)\) (la clase verdadera es \(g\)).

Si \(\hat{p}_{g}(x)\) es muy cercana a uno, deberíamos penalizar poco, pues dimos probabilidad alta a la clase \(g\) que ocurrió.
Si \(\hat{p}_{g}(x)\) es chica, deberíamos penalizar más, pues dimos probabilidad baja a observar la clase \(g\).
Si \(\hat{p}_{g}(x)\) es muy cercana a cero, y observamos \(g\), deberíamos hacer una penalización muy alta (convergiendo a \(\infty\), pues no es aceptable que sucedan eventos con probabilidad estimada extremadamente baja).

Quisiéramos encontrar una función \(h\) apropiada, de forma que la pérdida al observar \((x, g)\) sea \[s(\hat{p}_{g}(x)),\] y que cumpla con los puntos arriba señalados. Entonces tenemos que

\(s\) debe ser una función continua y decreciente en \([0,1]\)
Podemos poner \(s(1)=0\) (no hay pérdida si ocurre algo con que dijimos tiene probabilidad 1)
\(s(p)\) debe ser muy grande is \(p\) es muy chica.

Una opción analíticamente conveniente es \[s(p) = - \log(p)\]

s <- function(z){ -log(z) }
ggplot(tibble(p = (0:100) / 100), aes(x = p)) + 
    stat_function(fun = s) + ylab("Devianza")

Y entonces la pérdida (que llamamos pérdida logarítmica) que construimos está dada, para \((x,g)\) observado y probabilidades estimadas \(\hat{p}_g(x)\) por

\[ - \log(\hat{p}_g(x)) \]

donde \(\hat{p}(x)\) es la probabilidad estimada de nuestro modelo. Cuando ajustamos nuestro modelo, buscamos entonces encontrar los parámetros que minimizan la pérdida logarítmica.

Observaciones:

Ojo: a la pérdida logarítmica también se le llama de diferentes maneras en distintos lugares: entropía cruzada binaria o devianza (en este último caso, multipicada por 2)
Una razón importante para usar la pérdida logarítica como el objetivo a minimizar es que resulta en una estimación de máxima verosimilitud para los parámetros (condicional a las x’s), como veremos más adelante.
No es fácil interpretar la pérdida logarítmica, pero es útil para ajustar y comparar modelos. Veremos otras medidas más fáciles de interpretar más adelante.

Compara la siguiente definición con la que vimos para modelos de regresión:

Sea \[{\mathcal L}=\{ (x^{(1)},g^{(1)}),(x^{(2)},g^{(2)}), \ldots, (x^{(N)}, g^{(N)}) \}\] una muestra de entrenamiento, a partir de las cuales construimos mediante un algoritmo funciones estimadas \(\hat{p}_{g} (x)\) para \(g=0,1,\ldots, K-1\). La pérdida logarítmica promedio de entrenamiento está dada por \[\begin{equation} \overline{err} = - \frac{1}{N}\sum_{i=1}^N log(\hat{p}_{g^{(i)}} (x^{(i)})) \tag{8.1} \end {equation}\] Sea \[{\mathcal T}=\{ (x_0^{(1)},g_0^{(1)}),(x_0^{(2)},g_0^{(2)}), \ldots, (x_0^{(m)}, g_0^{(m)}) \}\] una muestra de prueba. La pérdida logarítmica de prueba es \[\begin{equation} \hat{Err} = - \frac{1}{m}\sum_{i=1}^m log(\hat{p}_{g_0^{(i)}} (x_0^{(i)})) \end {equation}\] que es una estimación de la pérdida logarítmica de predicción \[-E_{(x,g)}\left [ \log(\hat{p}_g(x)) \right ]\]

Ejemplo

Regresamos a nuestros ejemplo simulado de impago de tarjetas de crédito. Primero calculamos la devianza de entrenamiento

s <- function(x) -log(x)
dat_dev <- ajuste_vmc |> 
  predict(dat_ent, type = "prob") |> 
  bind_cols(dat_ent) |> 
  select(x, g, .pred_0, .pred_1)
dat_dev <- dat_dev |> mutate(hat_p_g = ifelse(g==1, .pred_1, .pred_0))

Nótese que dependiendo de qué clase observamos (columna \(g\)), extraemos la probabilidad correspondiente a la columna hat_p_g:

set.seed(125)
dat_dev |> sample_n(20)

## # A tibble: 20 × 5
##         x     g .pred_0 .pred_1 hat_p_g
##     <dbl> <int>   <dbl>   <dbl>   <dbl>
##  1 0.199      1  0.140    0.860  0.860 
##  2 0.674      1  0.502    0.498  0.498 
##  3 0.0518     1  0.0130   0.987  0.987 
##  4 0.785      1  0.530    0.470  0.470 
##  5 0.514      1  0.323    0.677  0.677 
##  6 0.116      1  0.0896   0.910  0.910 
##  7 0.504      0  0.309    0.691  0.309 
##  8 0.688      0  0.508    0.492  0.508 
##  9 0.749      0  0.523    0.477  0.523 
## 10 0.151      1  0.0685   0.931  0.931 
## 11 1          0  0.577    0.423  0.577 
## 12 0.0715     1  0.0254   0.975  0.975 
## 13 0.0893     1  0.0689   0.931  0.931 
## 14 0.328      1  0.213    0.787  0.787 
## 15 0.204      1  0.150    0.850  0.850 
## 16 0.679      0  0.503    0.497  0.503 
## 17 0.191      1  0.124    0.876  0.876 
## 18 0.182      1  0.106    0.894  0.894 
## 19 0.267      1  0.169    0.831  0.831 
## 20 0.0204     0  0.0523   0.948  0.0523

Ahora aplicamos la función \(s\) que describimos arriba, y promediamos sobre el conjunto de entrenamiento:

dat_dev <- dat_dev |> mutate(dev = s(hat_p_g))
dat_dev |> sample_n(20)

## # A tibble: 20 × 6
##          x     g .pred_0 .pred_1 hat_p_g    dev
##      <dbl> <int>   <dbl>   <dbl>   <dbl>  <dbl>
##  1 0.426       0  0.221    0.779  0.221  1.51  
##  2 0.0405      1  0.0264   0.974  0.974  0.0268
##  3 0.0371      1  0.0340   0.966  0.966  0.0345
##  4 0.377       0  0.217    0.783  0.217  1.53  
##  5 0.623       0  0.470    0.530  0.470  0.756 
##  6 0.155       1  0.0705   0.929  0.929  0.0732
##  7 0.155       1  0.0706   0.929  0.929  0.0732
##  8 0.118       1  0.0883   0.912  0.912  0.0925
##  9 0.506       0  0.311    0.689  0.311  1.17  
## 10 0.00410     1  0.0536   0.946  0.946  0.0551
## 11 0.150       1  0.0672   0.933  0.933  0.0696
## 12 0.00306     1  0.0536   0.946  0.946  0.0551
## 13 0.0703      1  0.0231   0.977  0.977  0.0234
## 14 0.300       1  0.199    0.801  0.801  0.222 
## 15 0.323       1  0.210    0.790  0.790  0.236 
## 16 0.109       1  0.0953   0.905  0.905  0.100 
## 17 0.00896     0  0.0537   0.946  0.0537 2.92  
## 18 1           0  0.577    0.423  0.577  0.551 
## 19 0.118       1  0.0887   0.911  0.911  0.0929
## 20 0.0358      1  0.0367   0.963  0.963  0.0374

dat_dev |> ungroup() |> summarise(dev_entrena = mean(dev))

## # A tibble: 1 × 1
##   dev_entrena
##         <dbl>
## 1       0.421

dat_dev |> mn_log_loss(factor(g, levels = c(1, 0)), .pred_1) |> 
  mutate(.estimate = .estimate)

## # A tibble: 1 × 3
##   .metric     .estimator .estimate
##   <chr>       <chr>          <dbl>
## 1 mn_log_loss binary         0.421

Recordemos que la devianza de entrenamiento no es la cantidad que evalúa el desempeño del modelo. Hagamos el cálculo entonces para una muestra de prueba:

set.seed(1213)
dat_prueba <- simular_impago(n = 5000) |> select(x, g)
## calcular para muestra de prueba
dat_dev_prueba <- ajuste_vmc |> 
  predict(dat_prueba, type = "prob") |> 
  bind_cols(dat_prueba) |> 
  select(x, g, .pred_0, .pred_1)
dat_dev_prueba <- dat_dev_prueba |> 
  mutate(hat_p_g = ifelse(g==1, .pred_1, .pred_0))
dat_dev_prueba <- dat_dev_prueba |> mutate(dev = s(hat_p_g))
dat_dev_prueba |> ungroup() |> summarise(dev_prueba = mean(dev))

## # A tibble: 1 × 1
##   dev_prueba
##        <dbl>
## 1      0.434

8.7 Regresión logística

En \(k\) vecinos más cercanos, intentamos estimar directamente con promedios las probabilidades de clase, sin considerar ninguna estructura. Ahora consideramos modelos más estructurados, definidos por parámetros, e intentaremos ajustarlos minimizando error logarítmico.

Igual que en regresión lineal, algunos de los modelos más simples que podemos imaginar son modelos lineales. Solo es necesario hacer una adaptación:

Supongamos que nuestra variable respuesta es \(y\), que toma valores 0 o 1.

Ahora queremos definir \(p(x) = p_1(x)\) (probabilidad de que ocurra la clase 1) en términos de un promedio ponderado de las variables de entrada, como en regresión lineal:

\[a_0 + a_1 x_1 + a_2 x_2 + \cdots + a_px_p.\]

Sin embargo, observamos que esta expresión puede dar valores negativos o mayores a uno, de forma que no necesariamente puede interpetarse como una probabilidad \(p(x)\). Una de las formas más sencillas de resolver este problema es transformar esta expresión para que necesariamente esté en \([0,1]\) por medio de una función fija \(h\):

\[p_{1}(x) = h(a_0 + a_1 x_1 + a_2 x_2 + \cdots + a_px_p),\] donde \(h\) debe ser una función que mapea valores reales a valores en \([0,1]\).

En este punto hay muchas funciones que podríamos usar. Para simplificar la interpretación y uso de este modelo, podemos escoger entre funciones que satisfagan, por ejemplo:

\(h\) toma valores en \([0,1]\) es creciente y diferenciable
\(h(0) = 0.5\) (0 equivale a probabilidad 0.5, negativos dan probabilidades menores a 0.5 y positivos dan probabilidades mayores a 0.5)
\(h(-x)=1-h(x)\) (simetría). Por ejemplo, si \(h(-2)=0.16\) entonces \(h(2)= 1-0.16=0.84\).

Hay todavía muchas opciones. Una de las más simples es usar la función logística

La función logística está dada por \[h(x)=\frac{e^x}{1+e^x}\]

h <- function(x){exp(x)/(1+exp(x)) }
ggplot(tibble(x = seq(-6, 6, 0.01)), aes(x = x)) + stat_function(fun = h)

Esta función comprime adecuadamente (para nuestros propósitos) el rango de todos los reales dentro del intervalo \([0,1]\). Si aplicamos al predictor lineal que consideramos, obtenemos:

El modelo de regresión logística está dado por \[p_1(x)=p_1(x;a)= h(a_0+a_1x_1 + a_2 x_2 + \cdots + a_p x_p)\]

y \[p_0(x)=p_0(x;a)=1-p_1(x;a),\] donde \(a=(a_0,a_1, a_2, \cdots, a_p)\).

Ejemplo

Consideremos nuestro ejemplo de impago. Podemos examinar qué tipo de probilidades obtendríamos con regresión logística y distintos parametros beta:

crear_p <- function(a_0, a_1){
    function(x){
        h(a_0 + a_1 * x)
    }
}
df_grid <- tibble(x = seq(0, 1, 0.01))
coefs_tbl <- tibble(a_0 = c(-5, -0.5, 2.5),
                a_1 = c(10, -2, -4))
graf_tbl <- coefs_tbl |> 
    mutate(p = map2(a_0, a_1, crear_p)) |> 
    mutate(grid = map(p, ~ df_grid |> mutate(p_1 = .(x)))) |> 
    select(-p) |> 
    mutate(fun_nom = paste(a_0, "+", a_1, "x")) |> 
    unnest(cols = c(grid))
graf_1 + geom_line(data = graf_tbl, aes(x = x, y = p_1)) + facet_wrap(~fun_nom)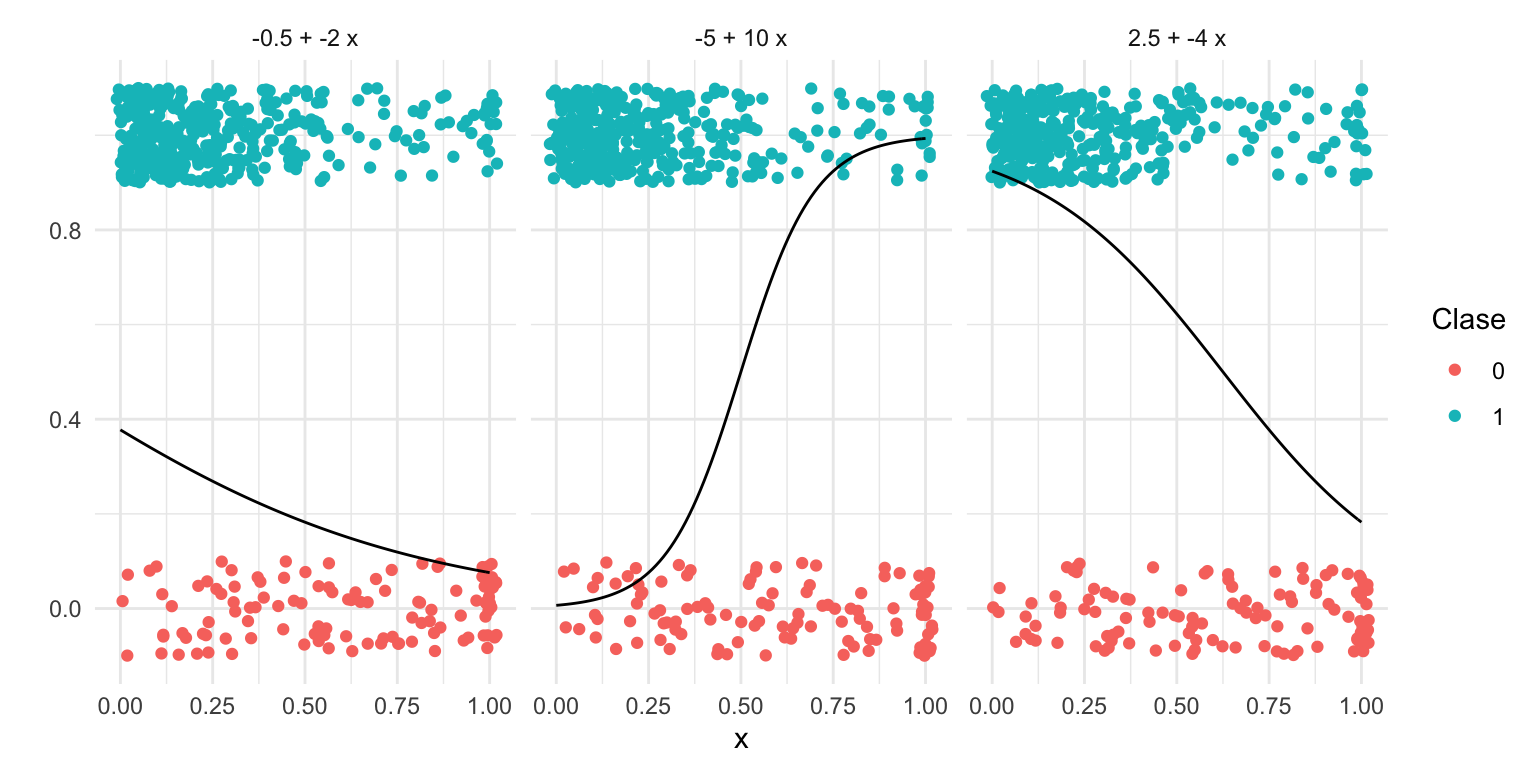

Experimenta con otros valores de \(a_0\) y \(a_1\).

8.8 Ejercicio: datos de diabetes

Ya están divididos los datos en entrenamiento y prueba

diabetes_ent <- as_tibble(MASS::Pima.tr)
diabetes_pr <- as_tibble(MASS::Pima.te)
diabetes_ent

## # A tibble: 200 × 8
##    npreg   glu    bp  skin   bmi   ped   age type 
##    <int> <int> <int> <int> <dbl> <dbl> <int> <fct>
##  1     5    86    68    28  30.2 0.364    24 No   
##  2     7   195    70    33  25.1 0.163    55 Yes  
##  3     5    77    82    41  35.8 0.156    35 No   
##  4     0   165    76    43  47.9 0.259    26 No   
##  5     0   107    60    25  26.4 0.133    23 No   
##  6     5    97    76    27  35.6 0.378    52 Yes  
##  7     3    83    58    31  34.3 0.336    25 No   
##  8     1   193    50    16  25.9 0.655    24 No   
##  9     3   142    80    15  32.4 0.2      63 No   
## 10     2   128    78    37  43.3 1.22     31 Yes  
## # … with 190 more rows

diabetes_ent$id <- 1:nrow(diabetes_ent)
diabetes_pr$id <- 1:nrow(diabetes_pr)

receta_diabetes <- recipe(type ~ ., diabetes_ent) |>
  update_role(id, new_role = "id_variable")

modelo_lineal <- logistic_reg(mode = "classification") |> 
  set_engine("glm")
flujo_diabetes <- workflow() |> 
  add_model(modelo_lineal) |> 
  add_recipe(receta_diabetes)
flujo_ajustado <- fit(flujo_diabetes, diabetes_ent)
flujo_ajustado

## ══ Workflow [trained] ══════════════════════════════════════════════════════════
## Preprocessor: Recipe
## Model: logistic_reg()
## 
## ── Preprocessor ────────────────────────────────────────────────────────────────
## 0 Recipe Steps
## 
## ── Model ───────────────────────────────────────────────────────────────────────
## 
## Call:  stats::glm(formula = ..y ~ ., family = stats::binomial, data = data)
## 
## Coefficients:
## (Intercept)        npreg          glu           bp         skin          bmi  
##   -9.773062     0.103183     0.032117    -0.004768    -0.001917     0.083624  
##         ped          age  
##    1.820410     0.041184  
## 
## Degrees of Freedom: 199 Total (i.e. Null);  192 Residual
## Null Deviance:       256.4 
## Residual Deviance: 178.4     AIC: 194.4

Ahora calculamos error logarítmico de prueba:

preds_prueba <- 
  predict(flujo_ajustado, diabetes_pr, type= "prob") |> 
  bind_cols(predict(flujo_ajustado, diabetes_pr)) |> 
  bind_cols(diabetes_pr |> select(type))
preds_prueba

## # A tibble: 332 × 4
##    .pred_No .pred_Yes .pred_class type 
##       <dbl>     <dbl> <fct>       <fct>
##  1    0.232    0.768  Yes         Yes  
##  2    0.960    0.0403 No          No   
##  3    0.975    0.0253 No          No   
##  4    0.959    0.0413 No          Yes  
##  5    0.204    0.796  Yes         Yes  
##  6    0.265    0.735  Yes         Yes  
##  7    0.590    0.410  No          Yes  
##  8    0.780    0.220  No          No   
##  9    0.558    0.442  No          No   
## 10    0.798    0.202  No          Yes  
## # … with 322 more rows

Nótese que tidymodels también da predicciones de clase simples, asignando a la clase de máxima probabilidad. Podemos estimar también qué tanto coincide esta clasificación con los valores observados (accuracy):

levels(preds_prueba$type)

## [1] "No"  "Yes"

# ponemos event_level si "positivo" no es el primer factor
metricas <- metric_set(accuracy, mn_log_loss)
metricas(preds_prueba, truth = type, .pred_Yes, estimate = .pred_class, 
         event_level = "second")

## # A tibble: 2 × 3
##   .metric     .estimator .estimate
##   <chr>       <chr>          <dbl>
## 1 accuracy    binary         0.801
## 2 mn_log_loss binary         0.441

Nota: concentrarse en predicciones de clase de esta forma generalmente no es buena idea al ajustar modelos o tomar decisiones de clasificación. Veremos más adelante cómo abordar el problema de tomar la decisión de clasificación.

8.9 Calibración de probabilidades

Adicionalmente a buscar pérdida logarítmica baja, cuando usamos las probabilidades obtenidas para más análisis o algún proceso, es necesario checar el ajuste. Podemos hacer esto realizando pruebas de la calibración de las probabilidades que arroja el modelo. Esto quiere decir que si el modelo nos dice que la probabilidad de que la clase 1 es 0.8, entonces si tenemos un número grande de estos casos (con probabilidad 0.8), alrededor de 80% de éstos tienen que ser positivos.

Ejemplo

Podemos checar la calibración de nuestro modelo para el ejemplo de diabetes.

dat_calibracion <- predict(flujo_ajustado, diabetes_pr, type = "prob") |> 
  bind_cols(diabetes_pr |> select(type)) |> 
  mutate(obs_yes = ifelse(type == "Yes", 1, 0))
dat_calibracion

## # A tibble: 332 × 4
##    .pred_No .pred_Yes type  obs_yes
##       <dbl>     <dbl> <fct>   <dbl>
##  1    0.232    0.768  Yes         1
##  2    0.960    0.0403 No          0
##  3    0.975    0.0253 No          0
##  4    0.959    0.0413 Yes         1
##  5    0.204    0.796  Yes         1
##  6    0.265    0.735  Yes         1
##  7    0.590    0.410  Yes         1
##  8    0.780    0.220  No          0
##  9    0.558    0.442  No          0
## 10    0.798    0.202  Yes         1
## # … with 322 more rows

ggplot(dat_calibracion, aes(x = .pred_Yes, y = obs_yes)) + 
    geom_jitter(width = 0, height = 0.02, alpha = 0.2) +
    geom_smooth(method = "loess", span = 0.75, colour = "red", se = FALSE) + 
    geom_abline() +
    coord_equal()

## `geom_smooth()` using formula 'y ~ x'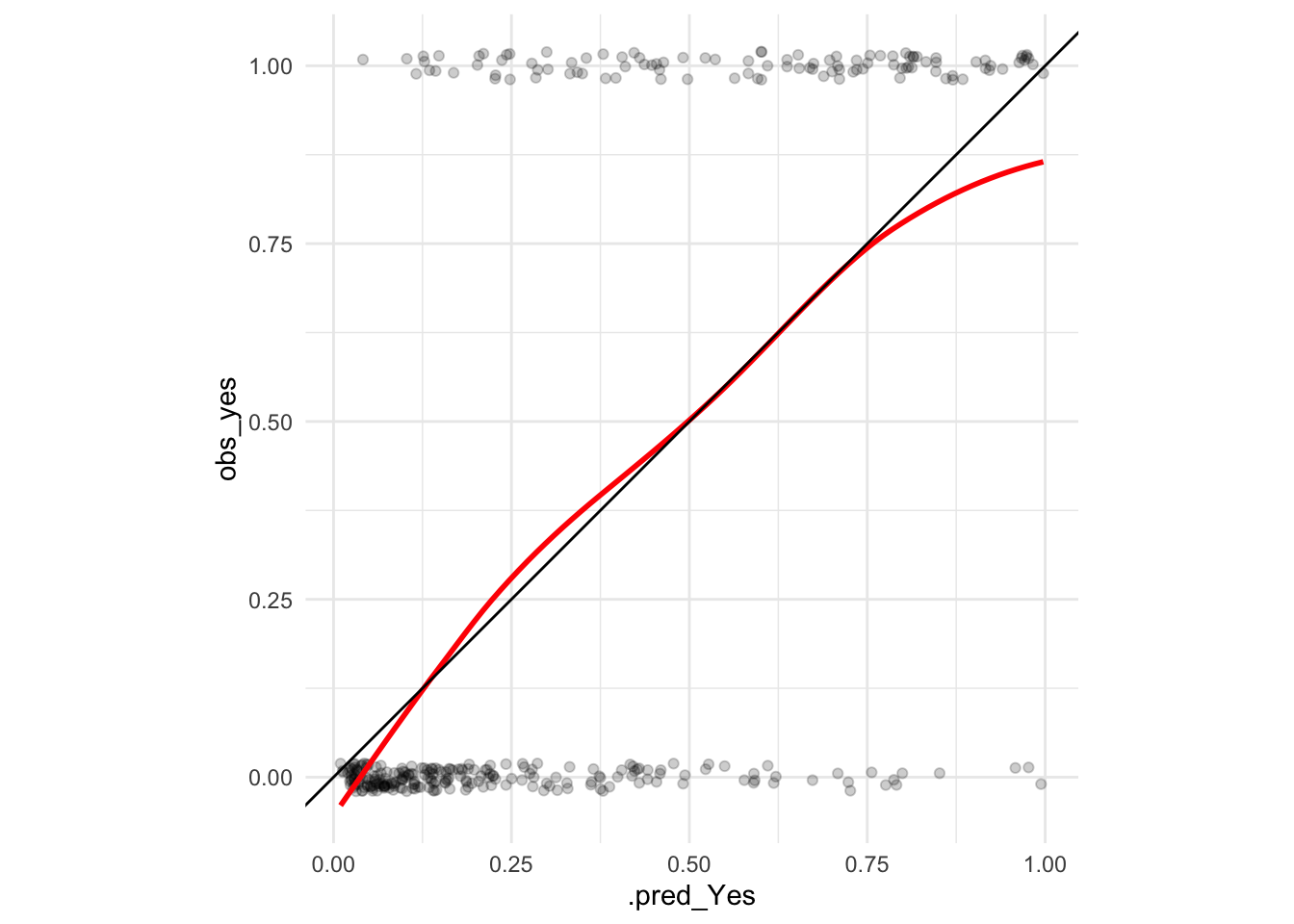

Y en esta gráfica verificamos que los promedios locales de proporciones de 0-1’s son consistentes con las probabilidades que estimamos. Otra manera de hacer esta gráfica es cortando las probabilidades en cubetas y calculamos intervalos de credibilidad para cada estimación: con esto checamos si el observado es consistente con las probabilidades de clase.

# usamos intervalos suavizados (bayesiano beta-binomial) en lugar de los basados
# en los errores estándar sqrt(p*(1-p) / n)
calibracion_gpos <- dat_calibracion |> 
    mutate(proba_grupo = cut(.pred_Yes, 
      quantile(.pred_Yes, seq(0, 1, 0.1)), include.lowest = TRUE)) |> 
    group_by(proba_grupo) |> 
    summarise(prob_media = mean(.pred_Yes), 
              n = n(),
              obs = sum(obs_yes), .groups = "drop") |> 
    mutate(obs_prop = (obs + 1) / (n + 2), 
           inferior = qbeta(0.05, obs + 1,  n - obs + 2),
           superior = qbeta(0.95, obs + 1,  n - obs + 2))
calibracion_gpos

## # A tibble: 10 × 7
##    proba_grupo      prob_media     n   obs obs_prop inferior superior
##    <fct>                 <dbl> <int> <dbl>    <dbl>    <dbl>    <dbl>
##  1 [0.00988,0.0412]     0.0289    34     0   0.0278  0.00142   0.0798
##  2 (0.0412,0.0714]      0.0574    33     1   0.0571  0.0102    0.129 
##  3 (0.0714,0.114]       0.0944    33     1   0.0571  0.0102    0.129 
##  4 (0.114,0.158]        0.136     33     6   0.2     0.0978    0.311 
##  5 (0.158,0.224]        0.191     33     4   0.143   0.0580    0.243 
##  6 (0.224,0.334]        0.276     33    12   0.371   0.236     0.496 
##  7 (0.334,0.454]        0.399     33    14   0.429   0.286     0.553 
##  8 (0.454,0.65]         0.548     33    17   0.514   0.365     0.635 
##  9 (0.65,0.805]         0.733     33    24   0.714   0.564     0.813 
## 10 (0.805,0.997]        0.901     34    30   0.861   0.730     0.925

ggplot(calibracion_gpos, 
  aes(x = prob_media, y = obs_prop, ymin = inferior, ymax = superior)) +
    geom_abline() +
    geom_linerange() +
    geom_point(colour = "red") + coord_equal() +
  xlab("Probabilidad de clase") +
  ylab("Proporción observada") +
  labs(subtitle = "Intervalos de 90% para prop observada")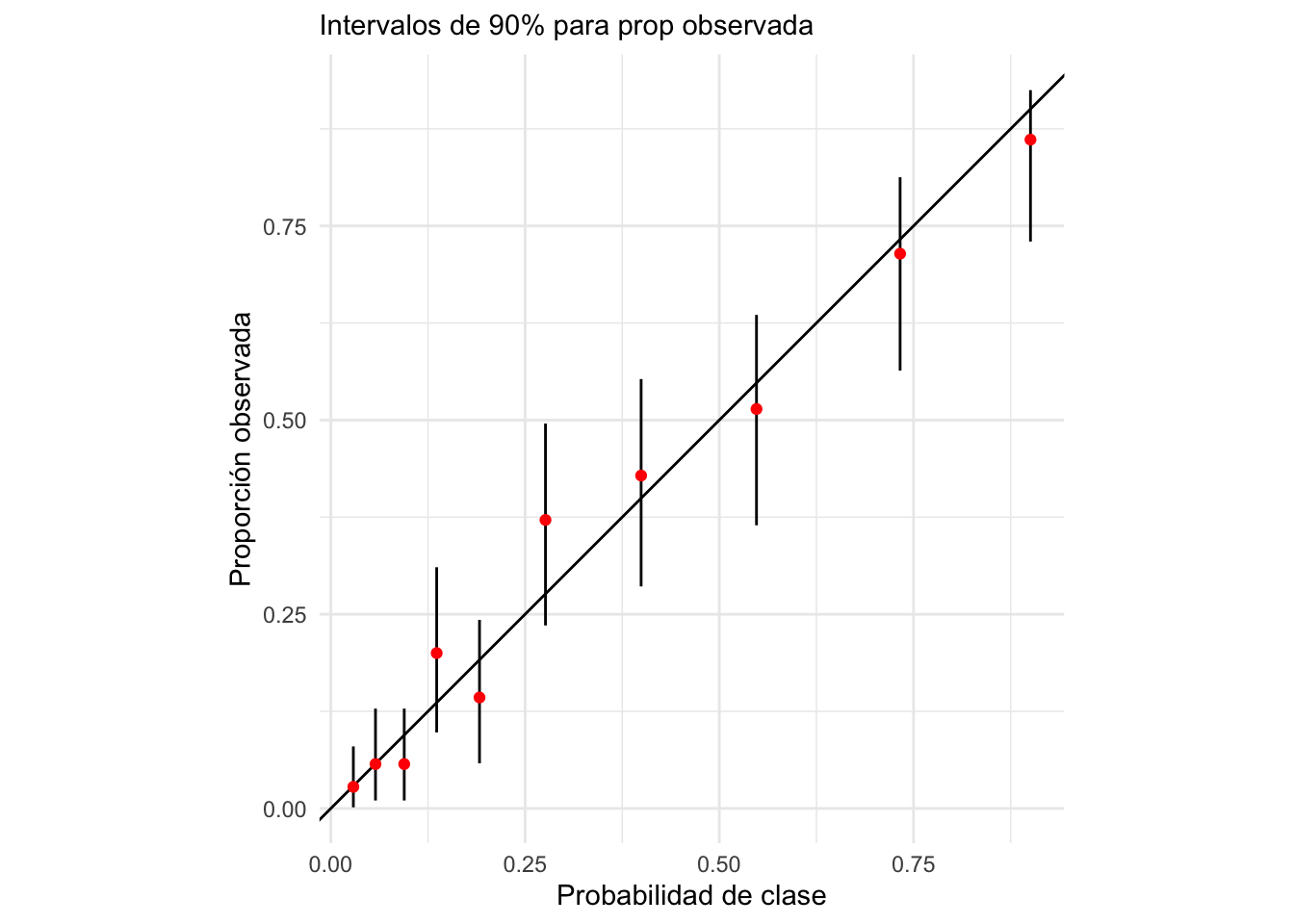

Y con esto verificamos que calibración del modelo es razonable. Observación: 1. Si las probabilidades no están calibradas, y las queremos utilizar como tales (con simplemente como scores), entonces puede ser necesario hacer un paso adicional de calibración, con una muestra separada de calibración (ver por ejemplo (kuhn?), sección 11.1). 2. En este ejemplo construimos intervalos para las proporciones observadas usando intervalos bayesianos. Es posible usar intervalos normales o t (usando el error estándar), pero estos intervalos tienen cobertura mala para proporciones muy chicas o muy grandes (https://en.wikipedia.org/wiki/Binomial_proportion_confidence_interval). Nuestro ejemplo es similar a los intervalos de Agresti-Coull.

8.10 Regularización para regresión logística

Podemos usar las mismas ideas regularización para modelos de regresión para respuesta numérica en el caso de regresión logística: la función objetivo original es la pérdida logarítmica, a la que podemos agregar una penalización tipo L1 o L2 para controlar varianza.

Ejemplo: clasificación de textos

En este ejemplo hacemos análisis de sentimiento, intentanto predecir si reseñas de películas son positivas o negativas a partir del texto de las reseñas. En este ejemplo veremos un enfoque relativamente simple, que consiste en considerar solamente las palabras que contienen las reseñas, sin tomar en cuenta el orden (el modelo de bolsa de palabras o bag of words).

Usaremos regresión logística regularizada.

Hay muchas maneras de preprocesar los datos para obtener variables numéricas a partir del texto. En este caso simplemente tomamos las palabras que ocurren más frecuentemente.

Encontramos las 3000 palabras más frecuentes sobre todos los textos, por ejemplo. Estas palabras son nuestro vocabulario.
Registramos en qué documentos ocurre cada una de esas palabras.
Cada palabra es una columna de nuestros datos, el valor es 1 si la palabra ocurre en documento y 0 si no ocurre.

Por ejemplo, para el texto “Un gato blanco, un gato negro”, “un perro juega”, “un astronauta juega” quedarían los datos:

texto_id	un	gato	negro	blanco	perro	juega
texto_1	1	1	1	1	0	0
texto_2	1	0	0	0	1	1
texto_3	1	0	0	0	0	1

Nótese que la palabra astronauta no está en nuestro vocabulario para este ejemplo.

Hay varias opciones para tener mejores variables, que pueden o no ayudar en este problema (no las exploramos en este ejercicio):

Usar conteos de frecuencias de ocurrencia de palabras en cada documento, o usar log(1+ conteo), en lugar de 0-1’s
Usar palabras frecuentes, pero quitar las que son stopwords, como son preposiciones y artículos entre otras, pues no tienen significado: en inglés, por ejemplo, so, is, then, the, a, etc.
Lematizar palabras: por ejemplo, contar en la misma categoría movie y movies, o funny y funniest, etc.
Usar indicadores binarios si la palabra ocurre o no en lugar de la frecuencia
Usar frecuencias ponderadas por qué tan rara es una palabra sobre todos los documentos (frecuencia inversa sobre documentos)
Usar pares de palabras en lugar de palabras sueltas: por ejemplo: juntar “not” con la palabra que sigue (en lugar de usar not y bad por separado, juntar en una palabra not_bad),
Usar técnicas de reducción de dimensionalidad que considera la co-ocurrencia de palabras (veremos más adelante en el curso).
Muchas otras

Los textos originales los puedes encontrarlos en la carpeta datos/sentiment. Están en archivos individuales que tenemos que leer. Podemos hacer lo que sigue:

# puedes necesitar el siguiente paquete
# install.packages("textrecipes")
# install.packages("stopwords")
nombres_neg <- list.files("./datos/sentiment/neg", full.names = TRUE)
nombres_pos <- list.files("./datos/sentiment/pos", full.names = TRUE)
# positivo
textos_pos <- tibble(texto = map_chr(nombres_pos, read_file), polaridad = "pos")
textos_neg <- tibble(texto = map_chr(nombres_neg, read_file), polaridad = "neg")
textos <- bind_rows(textos_pos, textos_neg)
nrow(textos)

## [1] 2000

table(textos$polaridad)

## 
##  neg  pos 
## 1000 1000

Y un fragmento del primer texto:

str_sub(textos$texto[[5]], 1, 300)

## [1] "moviemaking is a lot like being the general manager of an nfl team in the post-salary cap era -- you've got to know how to allocate your resources . \nevery dollar spent on a free-agent defensive tackle is one less dollar than you can spend on linebackers or safeties or centers . \nin the nfl , this l"

Particionamos la muestra:

set.seed(83224)
polaridad_particion <- initial_split(textos, 0.5)
textos_ent <- training(polaridad_particion)
textos_pr <- testing(polaridad_particion)
nrow(textos_ent)

## [1] 1000

Ahora hacemos feature engineering y limpieza:

# install.packages("textrecipes")
# install.packages("stopwords")
library(textrecipes)
receta_polaridad <- recipe(polaridad ~ ., textos_ent) |>
  step_mutate(texto = str_remove_all(texto, "[_()]")) |> 
  step_mutate(texto = str_remove_all(texto, "\n")) |> 
  step_mutate(texto = str_remove_all(texto, "[0-9]*")) |> 
  step_tokenize(texto) |> # separar por palabras
  step_stopwords(texto) |> 
  step_tokenfilter(texto, max_tokens = 6000) |> 
  step_tf(texto, weight_scheme = "raw count") 
# en el prep se separa en palabras, se eliminan stopwords,
# se filtran los de menor frecuencia y se crean las variables
# 0 - 1 que discutimos arriba, todo con los textos de entrenamiento

Los términos seleccionados (el vocabulario) están aquí (una muestra)

receta_prep <- receta_polaridad |> prep()
receta_prep$term_info |> sample_n(30)

## # A tibble: 30 × 4
##    variable              type    role      source 
##    <chr>                 <chr>   <chr>     <chr>  
##  1 tf_texto_ford         numeric predictor derived
##  2 tf_texto_upbeat       numeric predictor derived
##  3 tf_texto_ocean        numeric predictor derived
##  4 tf_texto_secondary    numeric predictor derived
##  5 tf_texto_holding      numeric predictor derived
##  6 tf_texto_movie's      numeric predictor derived
##  7 tf_texto_subsequently numeric predictor derived
##  8 tf_texto_hawke        numeric predictor derived
##  9 tf_texto_hunting      numeric predictor derived
## 10 tf_texto_glad         numeric predictor derived
## # … with 20 more rows

El tamaño de la matriz que usaremos para regresión logística tiene 1400 renglones (textos) por 6000 columnas de términos:

mat_textos_entrena <- juice(receta_prep) 
dim(mat_textos_entrena)

## [1] 1000 6001

head(mat_textos_entrena)

## # A tibble: 6 × 6,001
##   polaridad tf_texto_abandon tf_texto_abandon… tf_texto_abilit… tf_texto_ability
##   <fct>                <dbl>             <dbl>            <dbl>            <dbl>
## 1 pos                      0                 0                0                0
## 2 neg                      0                 0                0                0
## 3 pos                      0                 0                0                0
## 4 neg                      0                 0                0                0
## 5 neg                      0                 0                0                0
## 6 pos                      0                 0                0                0
## # … with 5,996 more variables: tf_texto_able <dbl>, tf_texto_aboard <dbl>,
## #   tf_texto_abraham <dbl>, tf_texto_absence <dbl>, tf_texto_absent <dbl>,
## #   tf_texto_absolute <dbl>, tf_texto_absolutely <dbl>,
## #   tf_texto_absorbing <dbl>, tf_texto_absurd <dbl>, tf_texto_abuse <dbl>,
## #   tf_texto_abyss <dbl>, tf_texto_academy <dbl>, tf_texto_accent <dbl>,
## #   tf_texto_accents <dbl>, tf_texto_accept <dbl>, tf_texto_acceptable <dbl>,
## #   tf_texto_acceptance <dbl>, tf_texto_accepted <dbl>, …

Ahora hacemos regresión lineal con regularización ridge/lasso (aunque este es un problema que podríamos tratar mejor con regresión logística). La penalización es de la forma

\[\lambda((1-\alpha) \sum_j \beta_j^2 + \alpha \sum_j |\beta_j|)\] de manera que combina ventajas de ridge (encoger juntos parámetros de variables correlacionadas) y lasso (eliminar variables que aportan poco a la predicción).

Primero intentamos un modelo con regularización baja:

textos_pr <- testing(polaridad_particion)
modelo_baja_reg <- logistic_reg(mixture = 0.5, penalty = exp(-10)) |> 
  set_engine("glmnet") |> set_mode("classification") |> 
  set_args(lambda.min.ratio = 1e-20)
flujo_textos <- workflow() |> 
  add_recipe(receta_polaridad) |> 
  add_model(modelo_baja_reg) |> 
  fit(textos_ent)
preds_baja_reg <- predict(flujo_textos, textos_pr, type = "prob") |> 
  bind_cols(textos_pr |> select(polaridad))

preds_baja_reg |> 
  mn_log_loss(factor(polaridad), .pred_pos, event_level = "second")

## # A tibble: 1 × 3
##   .metric     .estimator .estimate
##   <chr>       <chr>          <dbl>
## 1 mn_log_loss binary         0.606

Selecciona ahora un modelo con regularización mayor:

modelo_reg <- logistic_reg(mixture = 0.5, penalty = 0.05) |> 
  set_engine("glmnet") |> set_mode("classification") |> 
  set_args(lambda.min.ratio = 1e-20)
flujo_textos_reg <- workflow() |> 
  add_recipe(receta_polaridad) |> 
  add_model(modelo_reg) |> 
  fit(textos_ent)
preds_reg <- predict(flujo_textos_reg, textos_pr, type = "prob") |> 
  bind_cols(textos_pr |> select(polaridad))

Evaluamos:

preds_reg |> 
  mn_log_loss(factor(polaridad), .pred_pos, event_level = "second")

## # A tibble: 1 × 3
##   .metric     .estimator .estimate
##   <chr>       <chr>          <dbl>
## 1 mn_log_loss binary         0.462

El resultado es considerablemente mejor.

Examinamos ahora cómo son los coeficientes de nuestros modelos. Primero extraemos los modelos:

#por ejemplo:
coefs_baja <- flujo_textos |> extract_fit_parsnip() |> tidy() 
coefs_reg <- flujo_textos_reg |> extract_fit_parsnip() |> tidy() 
coefs_2mod <- bind_rows(coefs_baja, coefs_reg) |> 
  mutate(tipo = ifelse(penalty < 0.01, "coef_reg_baja", "coef_reg_alta")) |> 
  select(term, tipo, estimate) |> 
  pivot_wider(names_from = tipo, values_from = estimate)

Por ejemplo, podemos contrastar las palabras con coeficiente más positivo:

coefs_2mod |>  arrange(desc(coef_reg_baja)) |> select(term, coef_reg_baja) |> 
  head(20) |> gt()

term	coef_reg_baja
tf_texto_kicked	4.581457
tf_texto_musicians	3.697626
tf_texto_owned	3.259668
tf_texto_show's	3.043520
tf_texto_trials	2.956250
tf_texto_sappy	2.931601
tf_texto_openly	2.902903
tf_texto_buffs	2.595512
tf_texto_teams	2.437480
tf_texto_breathtaking	2.073268
tf_texto_searching	2.054267
tf_texto_believes	2.036386
tf_texto_midst	2.008365
tf_texto_collect	2.002440
tf_texto_nervous	1.978484
tf_texto_rooting	1.949066
tf_texto_strengths	1.933924
tf_texto_counselor	1.913895
tf_texto_instantly	1.879175
tf_texto_hilarious	1.825872

coefs_2mod |>  arrange(desc(coef_reg_alta)) |> select(term, coef_reg_alta) |> 
   head(20) |> gt()

term	coef_reg_alta
tf_texto_hilarious	0.4677061
tf_texto_owned	0.4296241
tf_texto_captures	0.3586261
tf_texto_edge	0.3442659
tf_texto_allows	0.3026168
tf_texto_outstanding	0.2911509
tf_texto_perfectly	0.2896178
tf_texto_believes	0.2811596
tf_texto_performances	0.2556436
tf_texto_subtle	0.2497019
tf_texto_maintains	0.2447731
tf_texto_age	0.2419194
tf_texto_excellent	0.2293933
tf_texto_absorbing	0.2217514
tf_texto_tender	0.2216957
tf_texto_crafted	0.2085651
tf_texto_terrific	0.1947051
tf_texto_overall	0.1924918
tf_texto_song	0.1745820
tf_texto_buffs	0.1725759

Ejercicio: repite para los coeficientes negativos.

8.11 Análisis de error para clasificadores

En muchos casos, podemos usar las probabilidades estimadas de calse para tomar decisiones acerca de los casos nuevos (por ejemplo, qué hacer si una transacción tiene probabilidad de fraude de 10% o de 5% o de 0.1% ?). Una manera simple de construir un clasificador (que toma una decisión de “predicción de clase”) es cortar a distintos niveles de probabilidad, lo que pretende reflejar qué tanto nos importa clasificar correctamente a los casos positivos o exluir a los casos negativos:

Si tenemos un modelo que estima probablidades de clase (para un problema binario), podemos construir distintos clasificadores (decisiones) usando distintos puntos de corte. Para cada \(0 < \alpha <1\), tenemos un clasificador \(\hat{G}_{\alpha}\) dado por:

Si \(p_1(x) > \alpha\), clasificamos el caso como positivo. En otro caso clasificamos como negativo.

Supondremos entonces que hemos construido un clasificador \(\hat{G}_\alpha\) a partir de probabilidades estimadas \(\hat{p}_1(x) > \alpha\). Por ejemplo, podemos construir el clasificador de Bayes clasificando como positivo a todos los casos \(x\) que cumplan \(\hat{p}_1(x) > 0.5\), y negativos al resto.

Hay dos tipos de errores en un clasificador binario (positivo - negativo):

Falsos positivos (fp): clasificar como positivo a un caso negativo.
Falsos negativos (fn): clasificar como negativo a un caso positivo.

A los casos clasificados correctamente les llamamos positivos verdaderos (pv) y negativos verdaderos (nv).

La matriz de confusión es entonces

tabla <- tibble(' ' = c('positivo.pred','negativo.pred','total'),
                    'positivo'=c('vp','fn','pos'),
                    'negativo'=c('fp','vn','neg'),
                    'total' = c('pred.pos','pred.neg',''))
knitr::kable(tabla)

	positivo	negativo	total
positivo.pred	vp	fp	pred.pos
negativo.pred	fn	vn	pred.neg
total	pos	neg

Nótese que un clasificador bueno, en general, es uno que tiene la mayor parte de los casos en la diagonal de la matriz de confusión.

Podemos estudiar a nuestro clasificador en términos de las proporciones de casos que caen en cada celda, que dependen del desempeño del clasificador en cuanto a casos positivos y negativos. La nomenclatura puede ser confusa, pues en distintas áreas se usan distintos nombres para estas proporciones:

Tasa de falsos positivos: proporción de veces que nos equivocamos en la clasificación para casos negativos. \[\frac{fp}{fp+nv}=\frac{fp}{neg}\]
Tasa de falsos negativos: proporción de veces que nos equivocamos en la clasificación para casos positivos. \[\frac{fn}{pv+fn}=\frac{fn}{pos}\]
Especificidad: tasa de correctos entre negativos, es el complemento de la tasa de falsos positivos. \[\frac{vn}{fp+vn}=\frac{vn}{neg}\]
Sensibilidad o Recall o Exhaustividad: tasa de correctos entre positivos, es el complemento de la tasa de falsos negativos. \[\frac{vp}{vp+fn}=\frac{vp}{pos}\]

También existen otras que tienen como base la clasificación en lugar de la clase verdadera, y en algunos casos estas ayudan en la interpretación:

Precisión o valor predictivo positivo: tasa de correctos entre todos los que clasificamos como positivos \[\frac{vp}{vp+fp}=\frac{vp}{pred.pos}\]
Valor predictivo negativo: tasa de correctos entre todos los que clasificamos como negativos \[\frac{vn}{fn+vn}=\frac{vn}{pred.neg}\]

Dependiendo de el tema y el objetivo hay medidas más naturales que otras:

En búsqueda y recuperación de documentos o imagenes, o detección de fraude ( donde positivo = el documento es relevante / la transacción es fraudulenta y negativo = el documento no es relevante / transacción normal), se usa más comunmente precisión y exhaustividad. La exhaustividad (recall o sensibilidad) es muy importante porque mide qué tan completa es la lista de resultados que entregamos. Pero para que el sistema sea utilizable (efectivo para el usuario), la mayor parte de los resultados entregados deben ser relevantes. Entonces es natural usal la precisión, que mide, entre todos los resultados con predicción positiva, que presentamos al usuario, qué porcentaje realmente son relevantes (precisión).

Un clasificador preciso es uno que tal que una fracción alta de sus predicciones positivas son positivos verdaderos. Sin embargo, podría no ser muy sensible: de todos los positivos que hay, solamente clasifica como positivos a una fracción chica. Conversamente, un clasificador podría ser muy sensible: captura una fracción alta de los positivos, pero también clasifica como positivos a muchos casos que son negativos (precisión baja).

En pruebas para detectar alguna enfermedad, muchas veces se utliza sensibilidad (recall o exhaustividad) y especificidad (qué proporción de negativos excluimos). Sensibilidad nos dice si estamos capturando a la mayoría de los verdaderos positivos. La especificidad nos dice qué tan bien estamos descartando casos que son verdaderos negativos. Si después de la prueba se propone algún tratamiento, estas dos cantidades nos dicen qué proporción de “enfermos” vamos a tratar y qué proporción de “sanos” vamos a tratar.

Cada clasificador tiene un balance distinto precisión y sensibilidad (o sensibilidad y especificidad) . Muchas veces no escogemos clasificadores por la tasa de incorrectos solamente, sino que intentamos buscar un balance adecuado entre el comportamiento de clasificación para positivos y para negativos.

Ejercicio

Calcular la matriz de confusión (sobre la muestra de prueba) para el clasificador logístico de diabetes en términos de imc y edad (usando punto de corte de 0.5). Calcula adicionalmente con la muestra de prueba sus valores de especificidad y sensibilidad, y precisión y recall.

receta_diabetes <- recipe(type ~ bmi + age, diabetes_ent) 
modelo_lineal <- logistic_reg(mode = "classification") |> 
  set_engine("glm")
flujo_diabetes <- workflow() |> 
  add_model(modelo_lineal) |> 
  add_recipe(receta_diabetes)
flujo_ajustado <- fit(flujo_diabetes, diabetes_ent)

Ahora probamos. Primero calculamos directamente:

preds_prueba <- predict(flujo_ajustado, diabetes_pr, type ='prob') |> 
  bind_cols(diabetes_pr)
# usar punto de corte 0.5
preds_prueba <- preds_prueba |> 
  mutate(clase_pred_g = ifelse(.pred_Yes > 0.5, "pred_Yes", "pred_No")) 
# calcular matriz de confusión
confusion <- preds_prueba |> 
  group_by(type, clase_pred_g) |> 
  count() |> pivot_wider(names_from = type, values_from = n) |> 
  ungroup() |> 
  column_to_rownames("clase_pred_g")
# en los renglones están las predicciones
confusion[c("pred_Yes", "pred_No"), ]

##           No Yes
## pred_Yes  29  42
## pred_No  194  67

Finalmente podemos calcular:

sensibilidad_1 <- confusion["pred_Yes", "Yes"] / sum(confusion[, "Yes"])
precision_1 <- confusion["pred_Yes", "Yes"] / sum(confusion["pred_Yes", ])
sprintf("Precisión: %.2f, Sensibilidad (recall): %.2f", precision_1, sensibilidad_1)

## [1] "Precisión: 0.59, Sensibilidad (recall): 0.39"

O también podemos hacer, usando tidymodels:

preds_prueba <- preds_prueba |> 
  mutate(clase_pred = ifelse(.pred_Yes > 0.5, "Yes", "No")) |> 
  mutate(clase_pred = factor(clase_pred, levels = c("No", "Yes")))
## calcular con yardstick
metricas_1 <- metric_set(accuracy, precision, recall)
preds_prueba |> 
  metricas_1(type, estimate = clase_pred, event_level = "second")

## # A tibble: 3 × 3
##   .metric   .estimator .estimate
##   <chr>     <chr>          <dbl>
## 1 accuracy  binary         0.711
## 2 precision binary         0.592
## 3 recall    binary         0.385

También podemos evaluar con sensibilidad y especificidad:

metricas_2 <- metric_set(accuracy, sens, spec)
preds_prueba |> 
  metricas_2(type, estimate = clase_pred, event_level = "second")

## # A tibble: 3 × 3
##   .metric  .estimator .estimate
##   <chr>    <chr>          <dbl>
## 1 accuracy binary         0.711
## 2 sens     binary         0.385
## 3 spec     binary         0.870

8.12 Análisis de error para probabilidades de clase

Con las métricas interpretables de la sección anterior (sensibilidad, especificidad, etc) es posible construir métricas resumen para evaluar probabilidades de clase. La idea general es:

Buscamos resúmenes que incorporen desempeño de todos los posibles clasificadores \(\hat{G}_{\alpha}\), usando las medidas de arriba de desempeño para clasificadores binarios.

Distintos valores de de \(\alpha\) dan distintos perfiles de sensibilidad-especificidad para una misma estimación de las probabilidades condicionales de clase: Para minimizar la tasa de incorrectos conviene poner \(\alpha= 0.5\). Sin embargo, es común que este no es el único fin de un clasificador bueno (pensar en ejemplo de fraude).

Cuando incrementamos \(\alpha\), quiere decir que exigimos estar más seguros de que un caso es positivo para clasificarlo como positivo. Esto quiere decir que la sensibilidad (recall) tiende a ser más chica. Por otro lado la precisión tiende a aumentar, pues el porcentaje de verdaderos positivos entre nuestras predicciones positivas será mayor. También la especificidad tiende a ser más grande.

Ejemplo

Por ejemplo, si en el caso de diabetes incrementamos el punto de corte a 0.7:

preds_prueba <- preds_prueba |> 
  mutate(clase_pred = ifelse(.pred_Yes > 0.7, "Yes", "No")) |> 
  mutate(clase_pred = factor(clase_pred, levels = c("No", "Yes")))
## calcular con yardstick
metricas <- metric_set(accuracy, precision, recall)
preds_prueba |> 
  metricas(type, estimate = clase_pred, event_level = "second")

## # A tibble: 3 × 3
##   .metric   .estimator .estimate
##   <chr>     <chr>          <dbl>
## 1 accuracy  binary         0.702
## 2 precision binary         0.656
## 3 recall    binary         0.193

La precisión mejora, pero la sensibilidad (recall) se deteriora. Visto desde el punto de vista de sensiblidad y especificidad:

preds_prueba |> 
  metricas_2(type, estimate = clase_pred, event_level = "second")

## # A tibble: 3 × 3
##   .metric  .estimator .estimate
##   <chr>    <chr>          <dbl>
## 1 accuracy binary         0.702
## 2 sens     binary         0.193
## 3 spec     binary         0.951

Cuando hacemos más chico \(\alpha\), entonces exigimos estar más seguros de que un caso es negativo para clasificarlo como negativo. Esto aumenta la sensibilidad, pero la precisión baja. Por ejemplo, si en el caso de diabetes ponemos el punto de corte en 0.3:

Ejemplo

preds_prueba <- preds_prueba |> 
  mutate(clase_pred = ifelse(.pred_Yes > 0.3, "Yes", "No")) |> 
  mutate(clase_pred = factor(clase_pred, levels = c("No", "Yes")))
## calcular con yardstick
metricas <- metric_set(accuracy, precision, recall)
preds_prueba |> 
  metricas(type, estimate = clase_pred, event_level = "second")

## # A tibble: 3 × 3
##   .metric   .estimator .estimate
##   <chr>     <chr>          <dbl>
## 1 accuracy  binary         0.657
## 2 precision binary         0.485
## 3 recall    binary         0.734

preds_prueba |> 
  metricas_2(type, estimate = clase_pred, event_level = "second")

## # A tibble: 3 × 3
##   .metric  .estimator .estimate
##   <chr>    <chr>          <dbl>
## 1 accuracy binary         0.657
## 2 sens     binary         0.734
## 3 spec     binary         0.619

Buscamos ahora hacer análisis de este tipo para todos los posibles puntos de corte. Dos técnicas son curvas ROC y curvas de precisión-exhaustividad, y medidas resumen asociadas.

8.13 Espacio ROC de clasificadores

Podemos visualizar el desempeño de cada uno de estos clasificadores construidos con puntos de corte mapeándolos a las coordenadas de tasa de falsos positivos (1-especificidad) y sensibilidad:

clasif_1 <- tibble(
  corte = c('0.3','0.5','0.7','perfecto','azar'),
  tasa_falsos_pos=c(0.24,0.08,0.02,0,0.7),
  sensibilidad =c(0.66, 0.46,0.19,1,0.7))
ggplot(clasif_1, aes(x=tasa_falsos_pos, y=sensibilidad,
  label=corte)) + geom_point() + 
  geom_abline(intercept=0, slope=1) +
  xlim(c(0,1)) +ylim(c(0,1)) + geom_text(hjust=-0.3, col='red')+
  xlab('1-especificidad (tasa falsos pos)')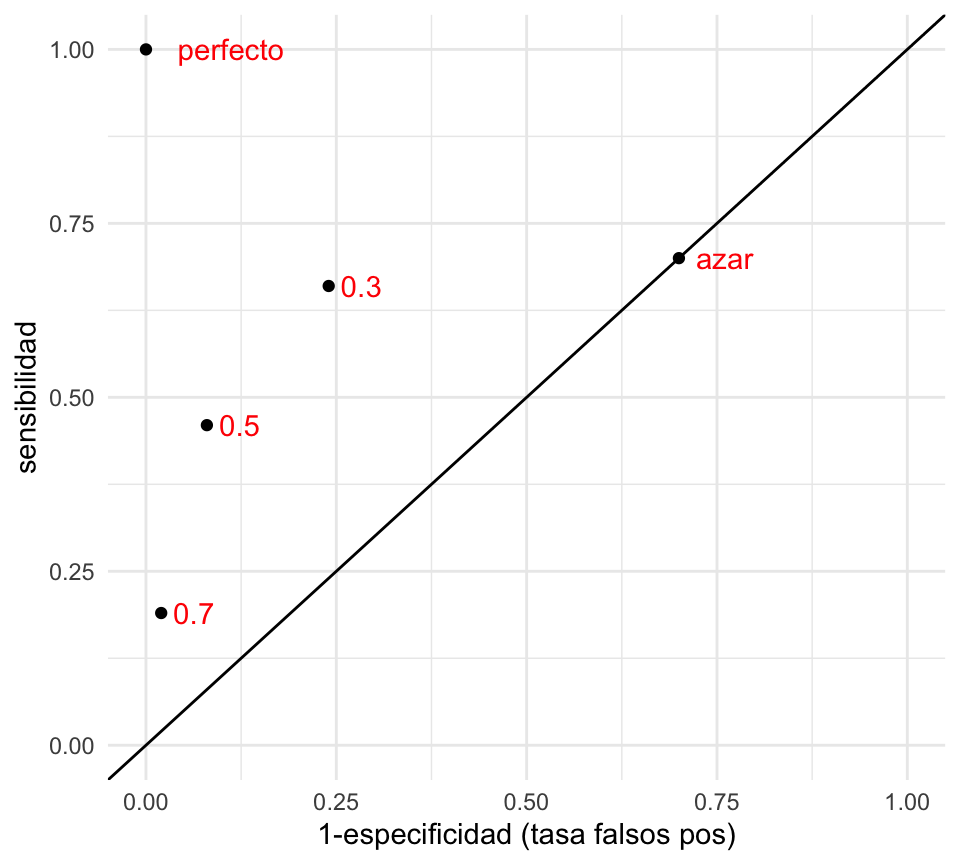

Nótese que agregamos otros dos clasificadores, uno perfecto, que tiene tasa de falsos positivos igual a 0 y sensibilidad igual a 1.
En esta gráfica, un clasificador \(G_2\) que está arriba a la izquierda de \(G_1\) domina a \(G_1\), pues tiene mejor especificidad y mejor sensibilidad. Entre los clasificadores 0.3, 0.5 y 0.7 de la gráfica, no hay ninguno que domine a otro.
Todos los clasificadores en la diagonal son equivalentes a un clasificador al azar. ¿Por qué? La razón es que si cada vez que vemos un nuevo caso lo clasificamos como positivo con probabilidad \(p\) fija y arbitraria. Esto implica que cuando veamos un caso positivo, la probabilidad de ’atinarle’ es de p (sensibilidad), y cuando vemos un negativo, la probabilidad de equivocarnos también es de 1-p (tasa de falsos positivos), por lo que la espcificidad es p también. De modo que este clasificador al azar está en la diagonal.
¿Qué podemos decir acerca de clasificadores que caen por debajo de la diagonal? Estos son clasificadores particularmente malos, pues existen clasificadores con mejor especificidad y/o sensibilidad que son clasificadores al azar! Sin embargo, se puede construir un mejor clasificador volteando las predicciones, lo que cambia sensibilidad por tasa de falsos positivos.
¿Cuál de los tres clasificadores es el mejor? En términos de la tasa de incorrectos, el de corte 0.5. Sin embargo, para otros propósitos puede ser razonable escoger alguno de los otros.

8.14 Perfil de un clasificador binario y curvas ROC

En lugar de examinar cada punto de corte por separado, podemos hacer el análisis de todos los posibles puntos de corte mediante la curva ROC (receiver operating characteristic, de ingeniería).

Para un problema de clasificación binaria, dadas estimaciones \(\hat{p}_1(x)\), la curva ROC grafica todos los pares de (1-especificidad, sensibilidad) para cada posible punto de corte \(\hat{p}_1(x) > \alpha\).

Ejemplo

roc_tbl <- roc_curve(preds_prueba, truth = type, estimate = .pred_Yes, 
                     event_level = "second")
roc_tbl

## # A tibble: 321 × 3
##    .threshold specificity sensitivity
##         <dbl>       <dbl>       <dbl>
##  1  -Inf          0                 1
##  2     0.0524     0                 1
##  3     0.0556     0.00448           1
##  4     0.0601     0.00897           1
##  5     0.0622     0.0135            1
##  6     0.0647     0.0224            1
##  7     0.0653     0.0269            1
##  8     0.0664     0.0314            1
##  9     0.0669     0.0359            1
## 10     0.0699     0.0404            1
## # … with 311 more rows

ggplot(roc_tbl, aes(x = 1 - specificity, y = sensitivity)) +
  geom_path(aes(colour = .threshold), size = 1.2) +
  geom_abline(colour = "gray") + 
  coord_equal() +
  xlab("Tasa de falsos positivos") + ylab("Sensibilidad")

En esta gráfica podemos ver todos los clasificadores posibles basados en las probabilidades de clase. Podemos usar estas curvas como evaluación de nuestros clasificadores, dejando para más tarde la selección del punto de corte, si esto es necesario (por ejemplo, dependiendo de los costos de cada tipo de error).

También podemos definir una medida resumen del desempeño de un clasificador según esta curva:

La medida AUC (area under the curve) para un clasificador es el área bajo la curva generada por los pares sensibilidad-especificidad de la curva ROC.

roc_auc(preds_prueba, type, .pred_Yes, event_level = "second")

## # A tibble: 1 × 3
##   .metric .estimator .estimate
##   <chr>   <chr>          <dbl>
## 1 roc_auc binary         0.761

Cuanto más cerca de uno es este valor, mejor discriminan las probabilidades.

También es útil para comparar modelos. Consideremos el modelo de los datos de diabetes que incluyen todas las variables:

receta_diabetes <- recipe(type ~ ., diabetes_ent) |> 
  update_role(id, new_role = "id_var")
modelo_lineal <- logistic_reg(mode = "classification") |> 
  set_engine("glm")
flujo_diabetes_todas <- workflow() |> 
  add_model(modelo_lineal) |> 
  add_recipe(receta_diabetes)
flujo_ajustado_todas <- fit(flujo_diabetes_todas, diabetes_ent)
preds_prueba_todas <- predict(flujo_ajustado_todas, diabetes_pr, type ='prob') |> 
  bind_cols(diabetes_pr)
preds_prueba_2 <- bind_rows(preds_prueba |> mutate(modelo = "IMC y edad"),
                            preds_prueba_todas |> mutate(modelo = "Todas")) |> 
  group_by(modelo)

Y graficamos juntas:

roc_2_tbl <- roc_curve(preds_prueba_2, type, .pred_Yes, event_level = "second")
ggplot(roc_2_tbl, aes(x = 1 - specificity, y = sensitivity)) +
  geom_path(aes(colour = modelo), size = 1.2) +
  geom_abline(colour = "gray") + 
  coord_equal() +
  xlab("Tasa de falsos positivos") + ylab("Sensibilidad")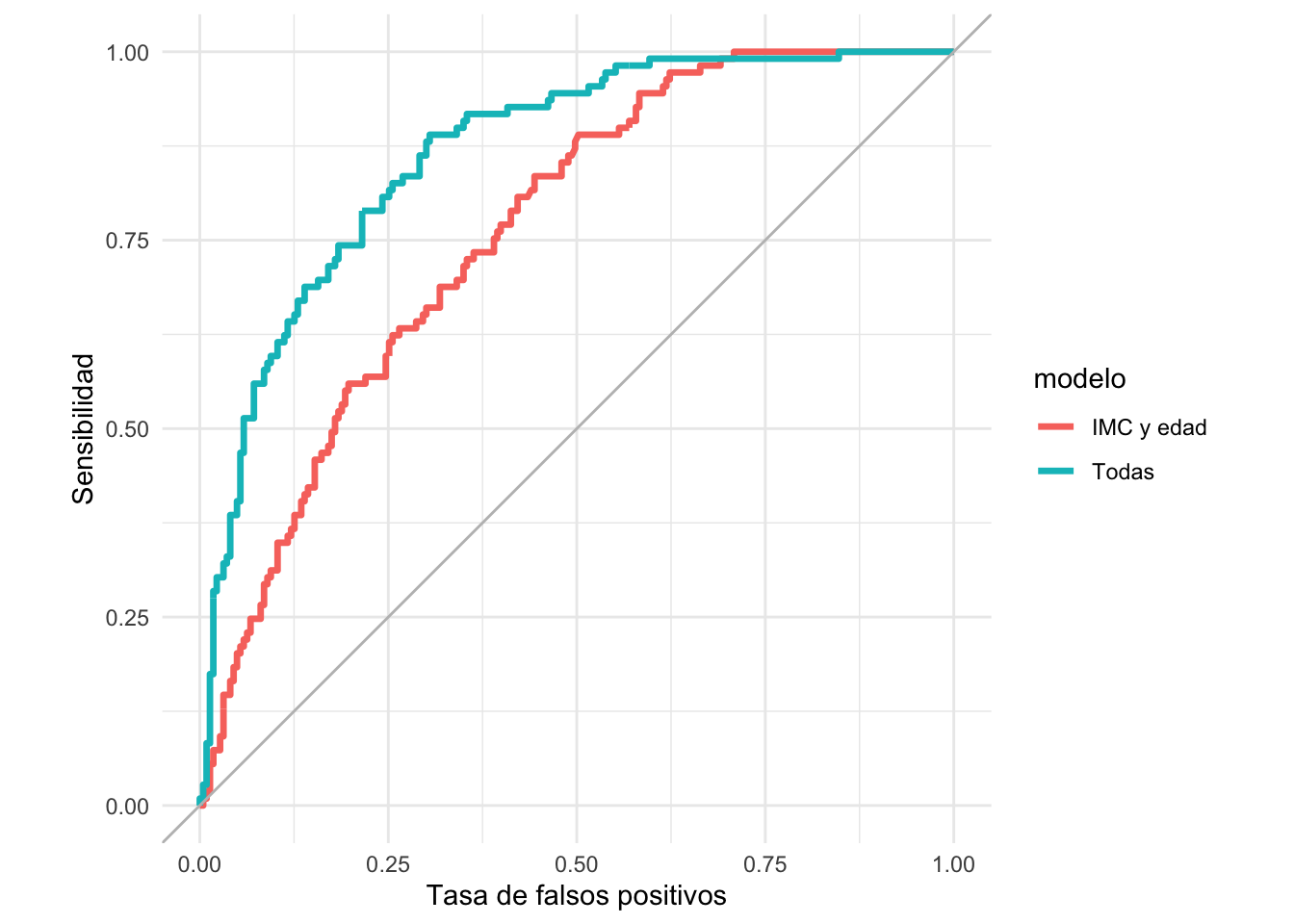

Comparación auc:

roc_auc(preds_prueba_2, type, .pred_Yes, event_level = "second")

## # A tibble: 2 × 4
##   modelo     .metric .estimator .estimate
##   <chr>      <chr>   <chr>          <dbl>
## 1 IMC y edad roc_auc binary         0.761
## 2 Todas      roc_auc binary         0.866

En este ejemplo, vemos que casi no importa qué perfil de especificidad y sensibilidad busquemos: el clasificador que usa todas las variables domina casi siempre al clasificador que sólo utiliza IMC y edad.

8.15 Curvas de precisión-sensibilidad

Para mostrar los posibles perfiles de clasificación de nuestro modelo, podemos mostrar las posibles combinaciones de precisión y recall bajo todos los posibles cortes:

pr_auc_tbl <- pr_curve(preds_prueba_2, type, .pred_Yes, event_level = "second")
ggplot(pr_auc_tbl |> filter(modelo != "Todas"), 
       aes(x = recall , y = precision)) +
  geom_path(aes(colour = .threshold), size = 1.2) +
  geom_abline(colour = "gray") + 
  coord_equal() +
  xlab("Exhaustividad (Sensibilidad)") + ylab("Precisión")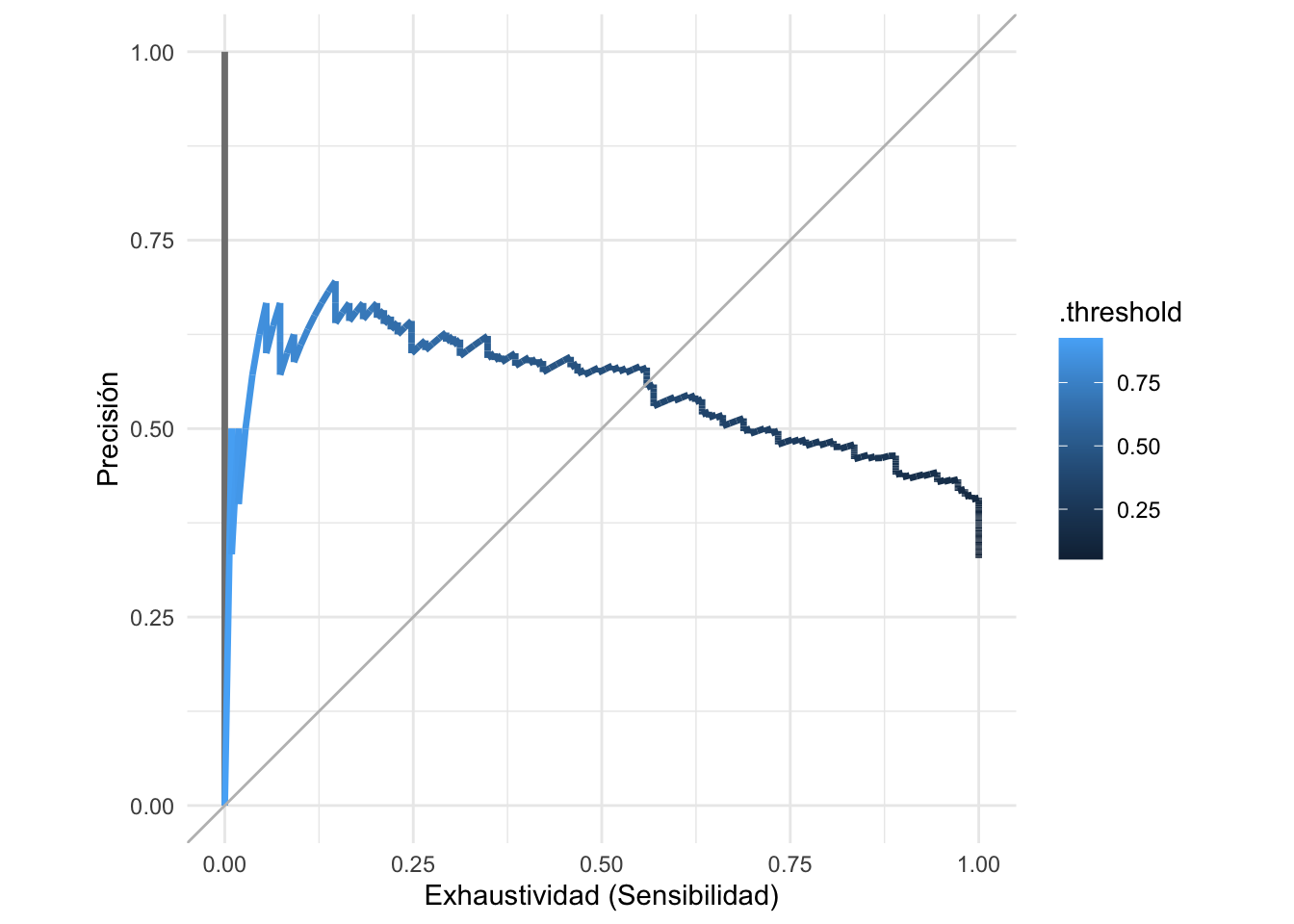

Nota que hay algunas oscilaciones en la curva. Cuando el punto de corte sube, la sensibilidad siempre baja o se queda igual (hay la misma cantidad o menos de verdaderos positivos). Sin embargo, la precisión se calcula sobre la base del número predicciones positivas, y esta cantidad siempre disminuye cuando el punto de corte aumenta. Especialmente cuando el número de predicciones positivas es chico, esto puede producir oscilaciones como las de la figura.

Ahora probamos usando todas las variables y comparamos

ggplot(pr_auc_tbl , 
       aes(x = recall , y = precision)) +
  geom_path(aes(colour = modelo), size = 1.2) +
  xlab("Exhaustividad (Sensibilidad)") + ylab("Precisión")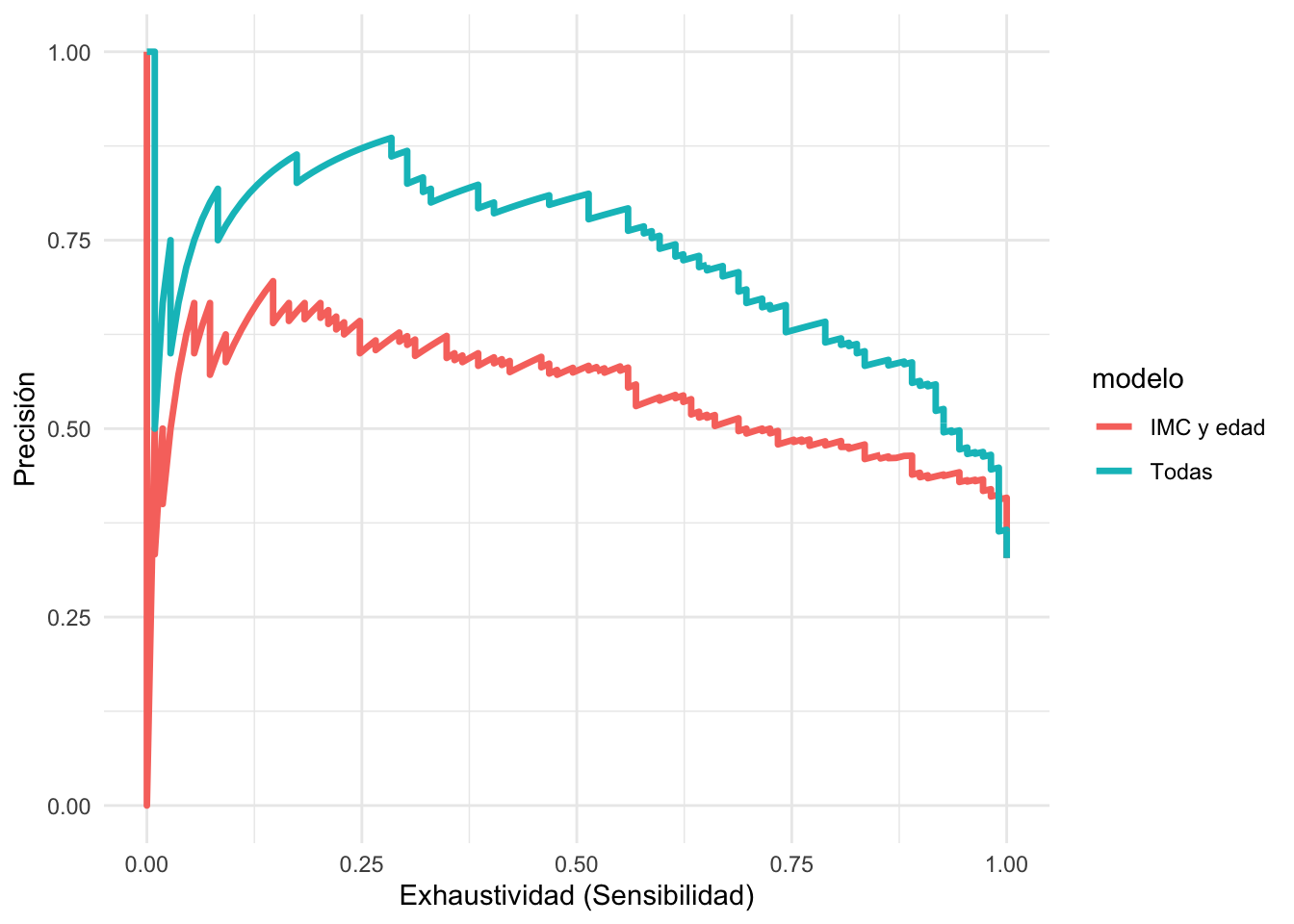

Y observamos que el modelo con todas las variables tiende a domina al modelo de IMC y edad.

Observaciones: - Precisión y Recall (sensibilidad) son medidas muy naturales para muchos problemas, en particular aquellos donde la clase de positivos es relativamente chica. - Sin embargo, en puntos de corte altos las estimaciones de precisión son ruidosas cuando nuestro conjunto de prueba es relativamente chico y no existen muchos casos con probabilidades altas (el denominador de precisión es el número de clasificados como positivos) - Una alternativa es usar curvas ROC

8.16 Curvas acumuladas de ganancia y lift

Otro enfoque común y útil es graficar en el eje horizontal el porcentaje de casos que cada clasificador clasifica como positivos para cada punto de corte- en términos de la decisión que nos interesa, esto usualmente indica qué porcentaje de los casos esperamos intervenir o probar (por ejemplo, el porcentaje que recibe una campaña publicitaria, o que califica para algún programa especial). En el eje vertical ponemos la sensibilidad, que es qué porcentaje de todos los positivos esperamos encontrar:

gain_tbl <- gain_curve(preds_prueba_2, type, .pred_Yes, event_level = "second")
ggplot(gain_tbl, 
       aes(x = .percent_tested , y = .percent_found)) +
  geom_path(aes(colour = modelo), size = 1.2) +
  geom_abline(colour = "gray") + 
  coord_equal() +
  xlab("% Clasificado positivo") + ylab("Sensibilidad")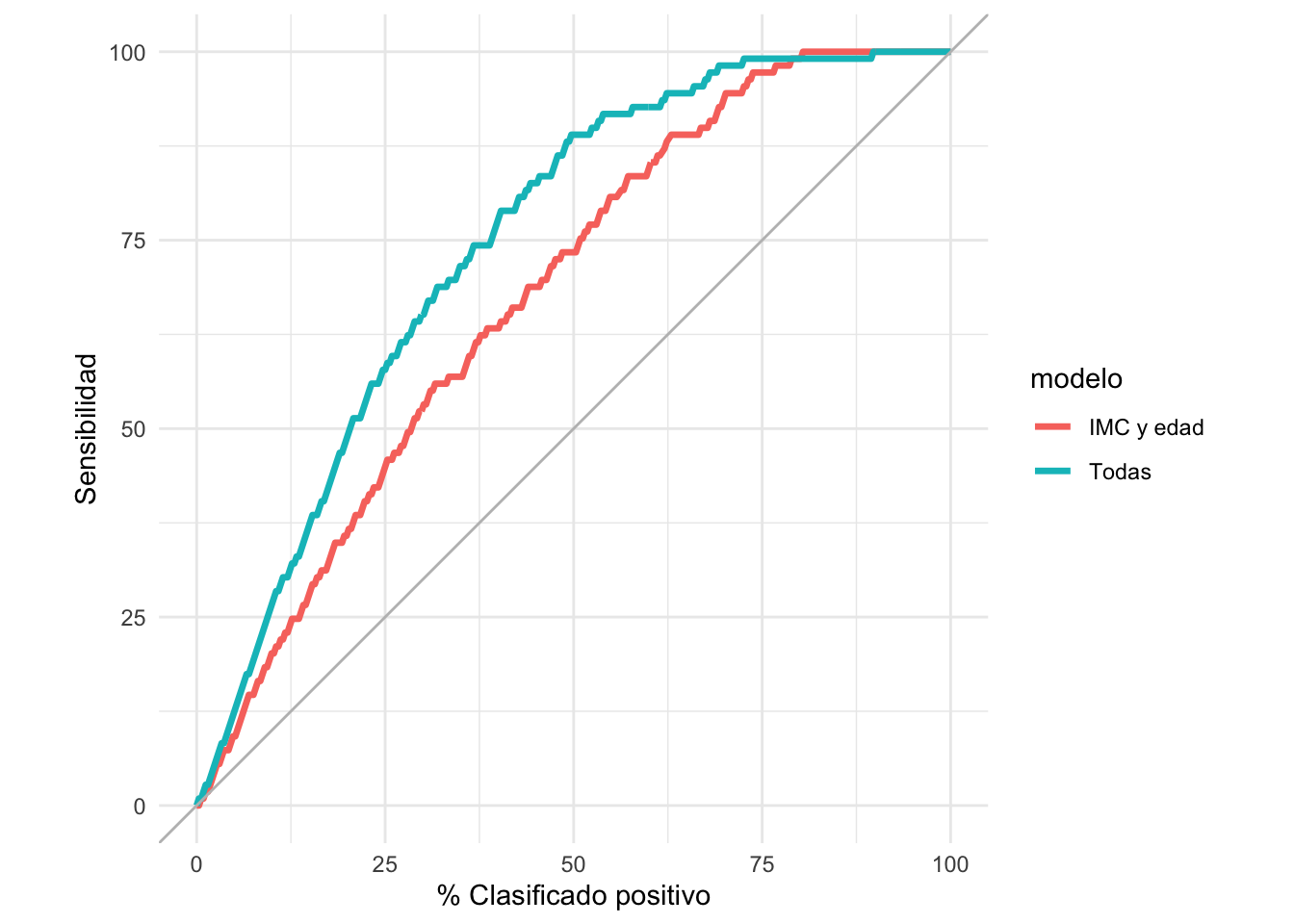

Y un análogo para las curvas de precisión-recall es la curva del lift. En el eje vertical graficamos la sensibilidad entre el % de clasificados como positivos (que es lo mismo que la precisión entre el % de casos positivos):

lift_tbl <- lift_curve(preds_prueba_2, type, .pred_Yes, event_level = "second")
ggplot(lift_tbl, 
       aes(x = .percent_tested , y = .lift)) +
  geom_path(aes(colour = modelo), size = 1.2) +
  xlab("% Clasificado positivo") + ylab("Lift")

## Warning: Removed 2 row(s) containing missing values (geom_path).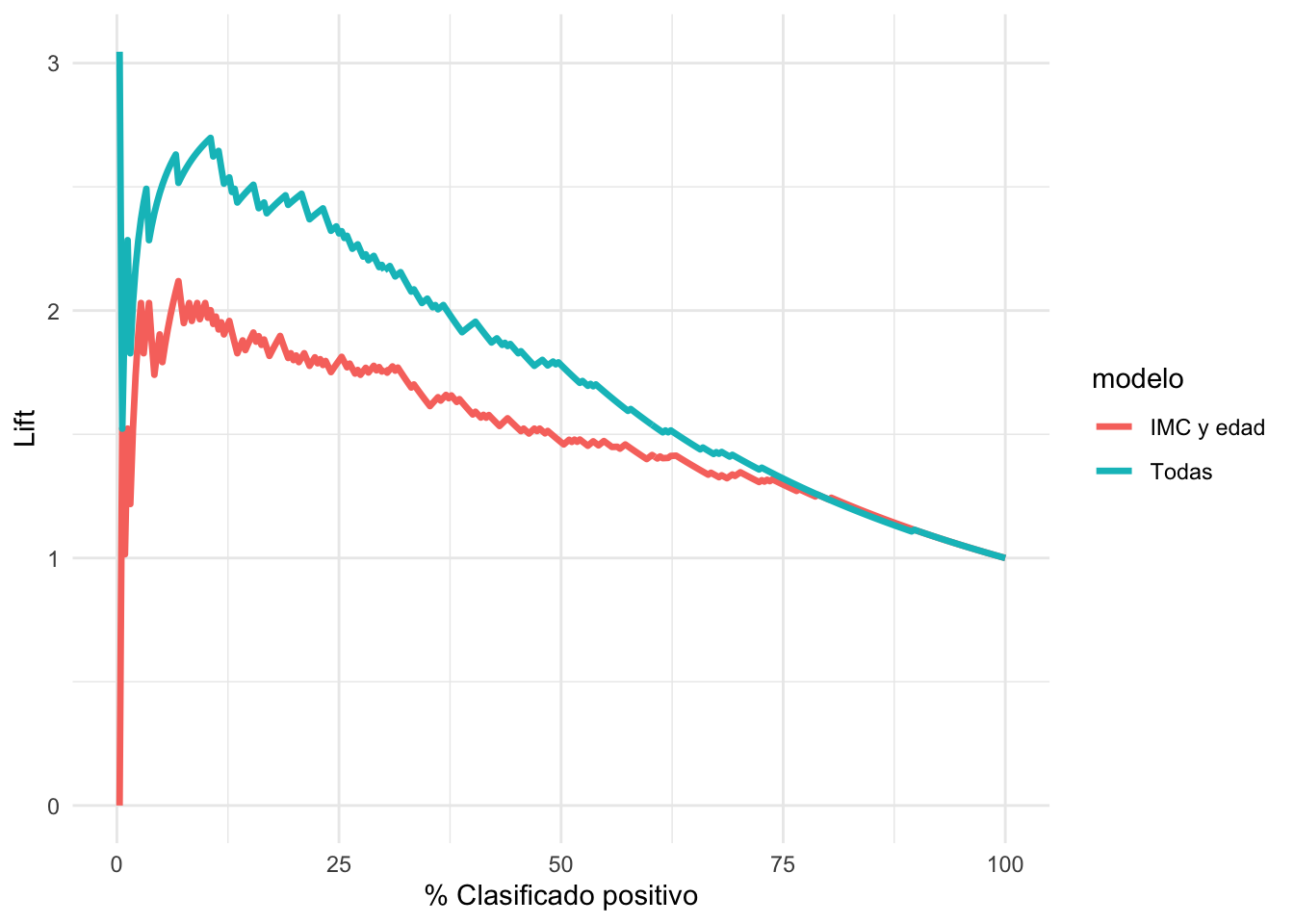

Cuando el lift es más grande que uno, quiere decir que el modelo es superior en encontrae positivos que una estrategia de tomar casos al azar. Por las mismas razones que las curvas de precisión-exhaustividad, la gráfica puede ser ruidosa para puntos de corte altos.

8.17 Resumen: análisis de error

Como hemos discutido antes, cómo usar las predicciones puede variar mucho dependiendo del problema particular, y usualmente requiere un análisis costo-beneficio más completo. Sin embargo, en la práctica, cuando estamos construyendo clasificadores, muchas veces no sabemos las aplicaciones particulares de los modelos predictivos que estamos construyendo, o no sabemos bien cuál es el balance de costos de los distintos tipos de errores. De esta forma:

Usamos medidas como perdida logarítmica y AUC para construir y seleccionar modelos.
Mostramos resultados interpretables de cómo se puede decidir la clasificación en términos de curvas ROC, curvas precisión-exhaustividad o alguna similar. Este primer análisis muchas veces es suficiente para decidir qué tan buenos o aplicables son nuestros modelos en distintos escenarios.
El análisis completo costo-beneficio puede hacerse posteriormente si es necesario, pero requiere general un esfuerzo más grande.

7 Selección y evaluación de modelos

9 Árboles de decisión