6 Regularizacion: controlando complejidad
Como vimos en el ejemplo anterior, en algunos casos podemos construir modelos lineales de complejidad considerable (por ejemplo, transformando variables, incluyendo interacciones). De manera que aún cuando muchas veces se considera un modelo lineal como “simple” o de “baja complejidad”, es posible que la variabilidad de las estimaciones sea grande y sobreajustar.
Veamos primero un ejemplo simulado.
6.1 Ejemplo: datos simulados y varianza
Considermeos un problema donde tenemos unas 100 entradas con 300 casos. Supondremos que la función verdadera es
\[f(x) = \sum_{j=1}^{100} a_j x_j\]
set.seed(28015)
a_vec <- rnorm(100, 0, 0.2)
a <- tibble(term = paste0('V', 1:length(a_vec)), valor = a_vec)
head(a)## # A tibble: 6 × 2
## term valor
## <chr> <dbl>
## 1 V1 -0.121
## 2 V2 0.0374
## 3 V3 -0.129
## 4 V4 0.240
## 5 V5 -0.00962
## 6 V6 -0.0443
sim_datos <- function(n, beta){
p <- nrow(beta)
mat_x <- matrix(rnorm(n * p, 0, 0.5), n, p) + rnorm(n, 0, 2)
colnames(mat_x) <- beta |> pull(term)
beta_vec <- beta |> pull(valor)
f_x <- mat_x %*% beta_vec
y <- as.numeric(f_x) + rnorm(n, 0, 1)
datos <- as_tibble(mat_x)
datos |> mutate(y = y)
}
set.seed(99121)
datos <- sim_datos(n = 4000, beta = a)
library(tidymodels)
separacion <- initial_split(datos, 0.03)
dat_ent <- training(separacion)
modelo <- linear_reg() |> set_engine("lm")
receta <- recipe(y ~ ., dat_ent)
flujo <- workflow() |>
add_model(modelo) |>
add_recipe(receta)
mod_1 <- fit(flujo, dat_ent) |> extract_fit_parsnip()
coefs_1 <- tidy(mod_1) |>
left_join(a)## Joining, by = "term"
ggplot(coefs_1 |> filter(term != "(Intercept)"),
aes(x = valor, y = estimate)) +
geom_point() +
xlab('Coeficientes') +
ylab('Coeficientes estimados') +
geom_abline() 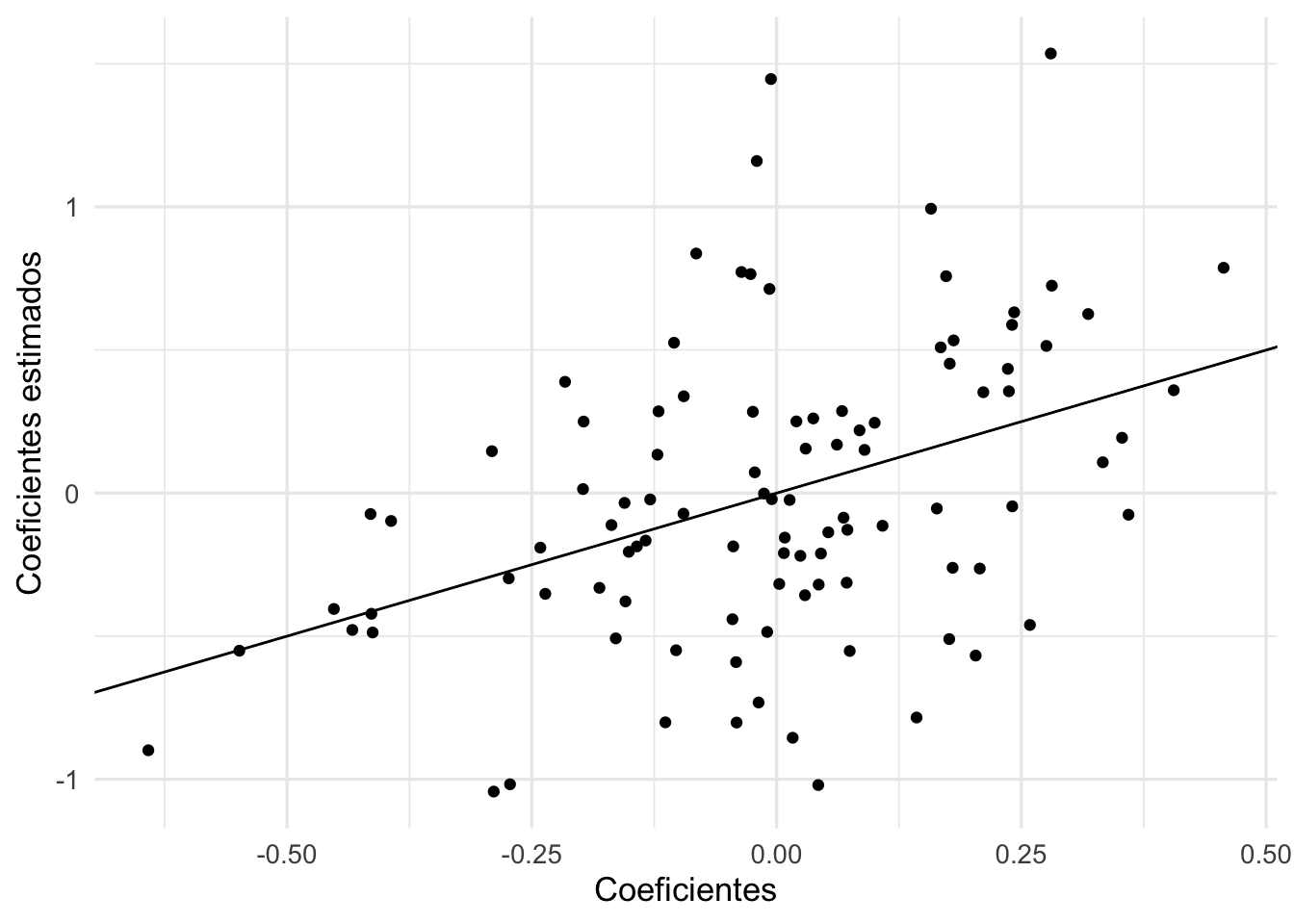
Y notamos que las estimaciones no son buenas. Podemos hacer otra simulación para confirmar que el problema es que las estimaciones son muy variables.
Con otra muestra de entrenamiento, vemos que las estimaciones tienen varianza alta.
datos_ent_2 <- sim_datos(n = 120, beta = a)
mod_2 <- fit(flujo, datos_ent_2) |> extract_fit_parsnip()
coefs_2 <- tidy(mod_2)
qplot(coefs_1$estimate, coefs_2$estimate) + xlab('Coeficientes mod 1') +
ylab('Coeficientes mod 2') +
geom_abline(intercept=0, slope =1)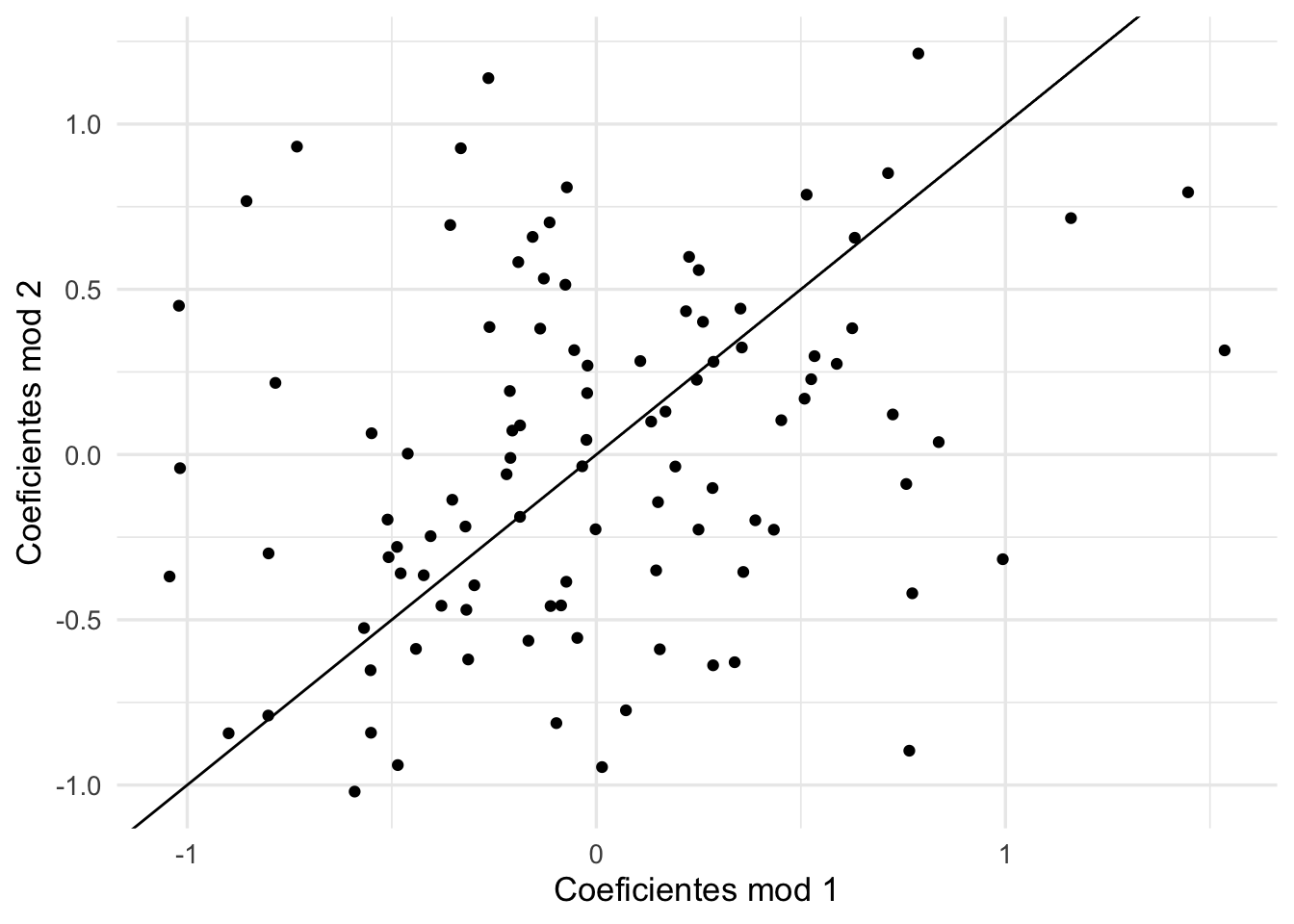
En la práctica, nosotros tenemos una sola muestra de entrenamiento. Así que, con una muestra de tamaño
\(n=250\) como en este ejemplo, obtendremos típicamente resultados no muy buenos. Estos coeficientes ruidosos afectan nuestras predicciones de manera negativa, aún cuando el modelo ajustado parece reproducir razonablemente bien la variable respuesta:
library(patchwork)
dat_pr <- testing(separacion)
p_entrena <- predict(mod_1, dat_ent) |>
bind_cols(dat_ent |> select(y))
p_prueba <- predict(mod_1, dat_pr) |>
bind_cols(dat_pr |> select(y))
g_1 <- ggplot(p_entrena, aes(x = .pred, y = y)) +
geom_abline(colour = "red") +
geom_point() +
xlab("Predicción") + ylab("y") +
labs(subtitle = "Muestra de entrenamiento")
g_2 <- ggplot(p_prueba, aes(x = .pred, y = y)) +
geom_abline(colour = "red") +
geom_point() +
xlab("Predicción") + ylab("y") +
labs(subtitle = "Muestra de prueba")
g_1 + g_2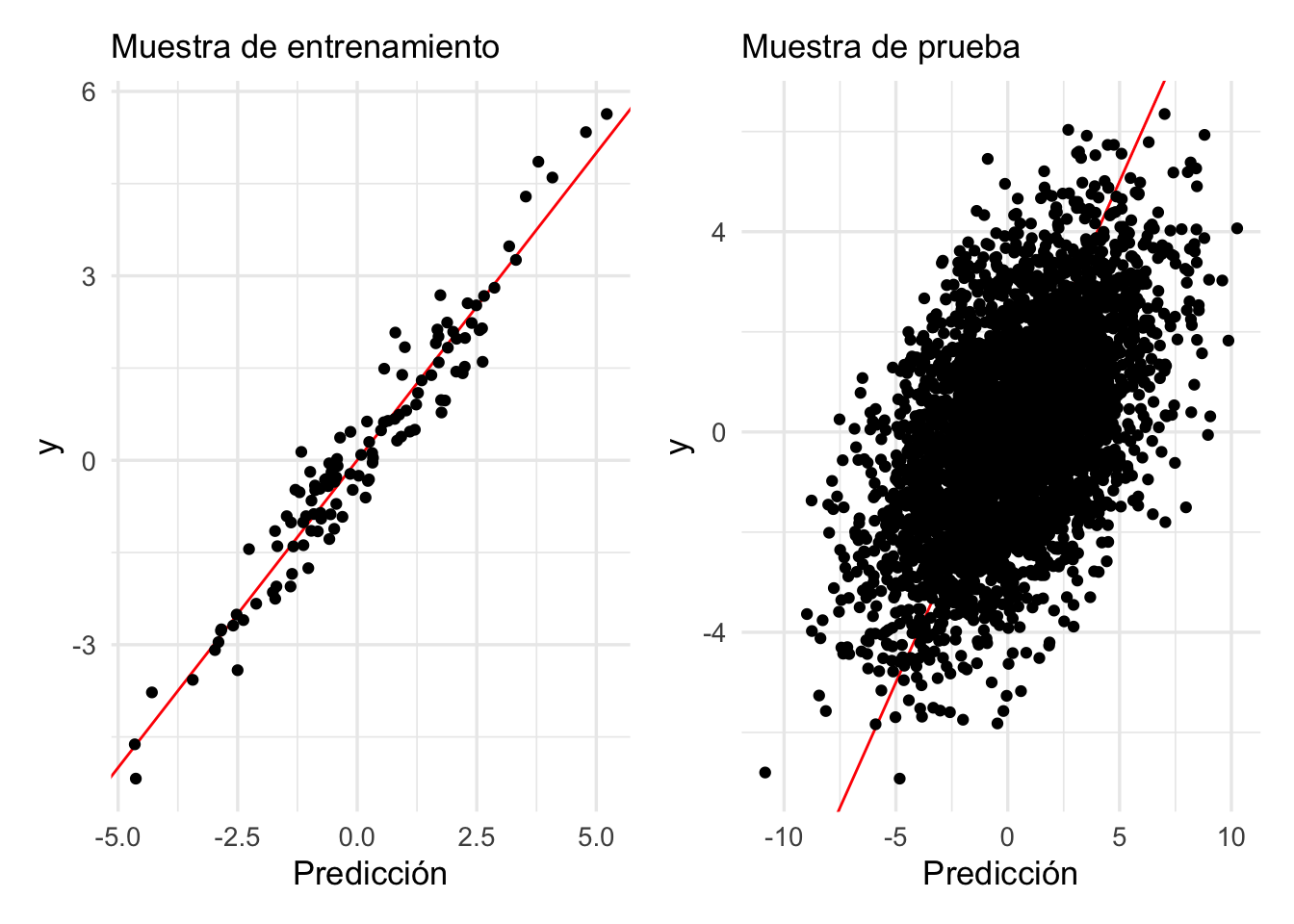
6.2 Penalización para controlar varianza
Como el problema es la variabilidad de los coeficientes (en este ejemplo no hay sesgo pues conocemos el modelo verdadero), podemos atacar este problema poniendo restricciones a los coeficientes, de manera que caigan en rangos más aceptables.
Una manera de hacer esto es restringir el rango de los coeficientes cambiando la función que minimizamos para ajustar el modelo lineal. Recordamos que la cantidad que queremos minimizar es
\[D(a) = D(a_0, a_1, \ldots, a_p) = \sum_{i=1}^N (y^{(i)} - f_a (x^{(i)}))^2 = \sum_{i=1}^N (y^{(i)} - a_0 - a_1 x_1^{(i)}-a_2x_2^{(i)} - \cdots - a_px_p^{(i)})^2\]
donde la suma es sobre los datos de entrenamiento. Queremos encontrar \(a =(a_0, a_1, \ldots, a_p)\) para resolver
\[\min_a D(a)\]
En el ejemplo que estamos considerando, vemos que existe mucha variación en los coeficientes obtenidos de muestra de entrenamiento a muestra de entrenamiento, y que algunos de ellos toman valores muy grandes positivos o negativos. Podemos entonces intentar resolver mejor el problema penalizado
\[\min_a D(a) + \lambda \sum_{j=1}^p a_j^2\]
Si escogemos un valor relativamente grande de \(\lambda > 0\), entonces
terminaremos con una solución donde los coeficientes
no pueden alejarse mucho de 0, y esto previene parte del sobreajuste que observamos en nuestro primer ajuste.
Otra manera de decir esto es: intentamos minimizar cuadrados, pero no permitimos que los coeficientes se alejen demasiado de cero, o ponemos un costo a soluciones que intentan “mover” mucho los coeficientes para ajustar mejor al conjunto de entrenamiento.
- Normalmente normalizamos las variables de entrada \(x\) para que tenga sentido normalizar todos los coeficientes con una misma \(\lambda\).
- También es posible poner restricciones sobre el tamaño de \(\sum_j a_j^2\), lo cual es equivalente al problema de penalización.
- Usualmente no penalizamos la constante \(a_0\), de forma que si \(\lambda\) es muy grande, nuestro modelo ajustado predice simplemente la media de los datos de entrenamiento.
- Este tipo de penalización se llama muchas veces \(L_2\), o penalización ridge.
6.3 Ejemplo: penalización ridge
En este caso obtenemos:
modelo_reg <- linear_reg(mixture = 0, penalty = 0.1) |>
set_engine("glmnet")
flujo_reg <- workflow() |>
add_model(modelo_reg) |>
add_recipe(receta)
flujo_reg <- fit(flujo_reg, dat_ent)
mod_reg <- flujo_reg |> extract_fit_parsnip()Los coeficientes del modelo penalizado son:
coefs_penalizado <- tidy(mod_reg) ## Loading required package: Matrix##
## Attaching package: 'Matrix'## The following objects are masked from 'package:tidyr':
##
## expand, pack, unpack## Loaded glmnet 4.1-2
coefs_penalizado## # A tibble: 101 × 3
## term estimate penalty
## <chr> <dbl> <dbl>
## 1 (Intercept) 0.137 0.1
## 2 V1 -0.0514 0.1
## 3 V2 0.0775 0.1
## 4 V3 -0.0923 0.1
## 5 V4 0.260 0.1
## 6 V5 -0.106 0.1
## 7 V6 0.156 0.1
## 8 V7 -0.172 0.1
## 9 V8 0.0140 0.1
## 10 V9 0.00267 0.1
## # … with 91 more rowsNótese que efectivamente la suma de cuadrados de los coeficientes penalizados es considerablemente más chica que las del modelo no penalizado:
sum(coefs_penalizado$estimate[-1]^2)## [1] 1.530926
sum(coefs_1$estimate[-1]^2)## [1] 27.02638Los nuevos coeficientes estimados tienen menor variación, y están más cercanos a los valores reales:
qplot(coefs_1$estimate, coefs_penalizado$estimate) +
xlab('Coeficientes') +
ylab('Coeficientes estimados') +
geom_abline()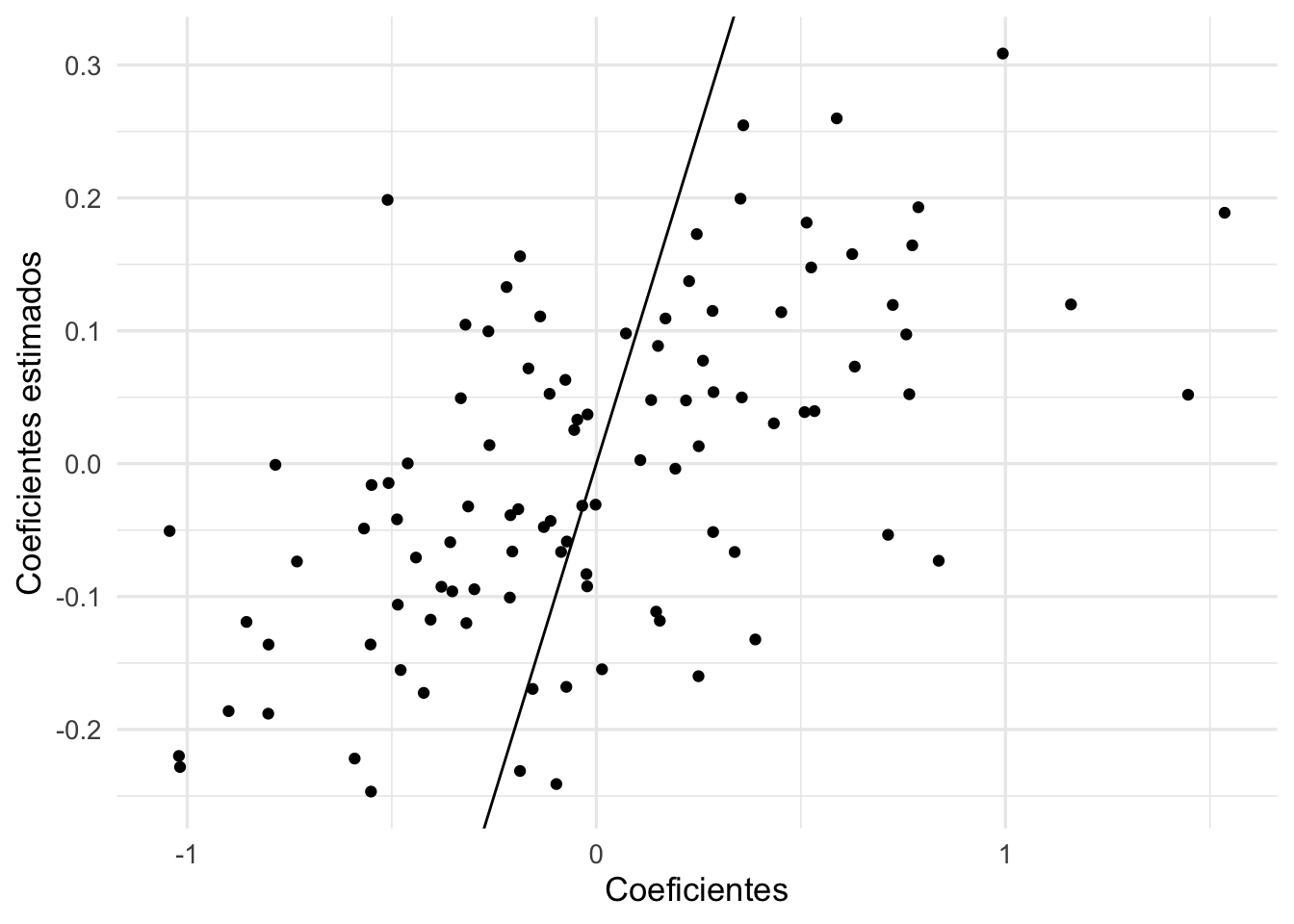
p_prueba_2 <- predict(mod_reg, dat_pr) |>
bind_cols(dat_pr |> select(y))
g_3 <- ggplot(p_prueba_2, aes(x = .pred, y = y)) +
geom_abline(colour = "red") +
geom_point() +
xlab("Predicción") + ylab("y") +
labs(subtitle = "Muestra de prueba - penalizado")
g_2 + g_3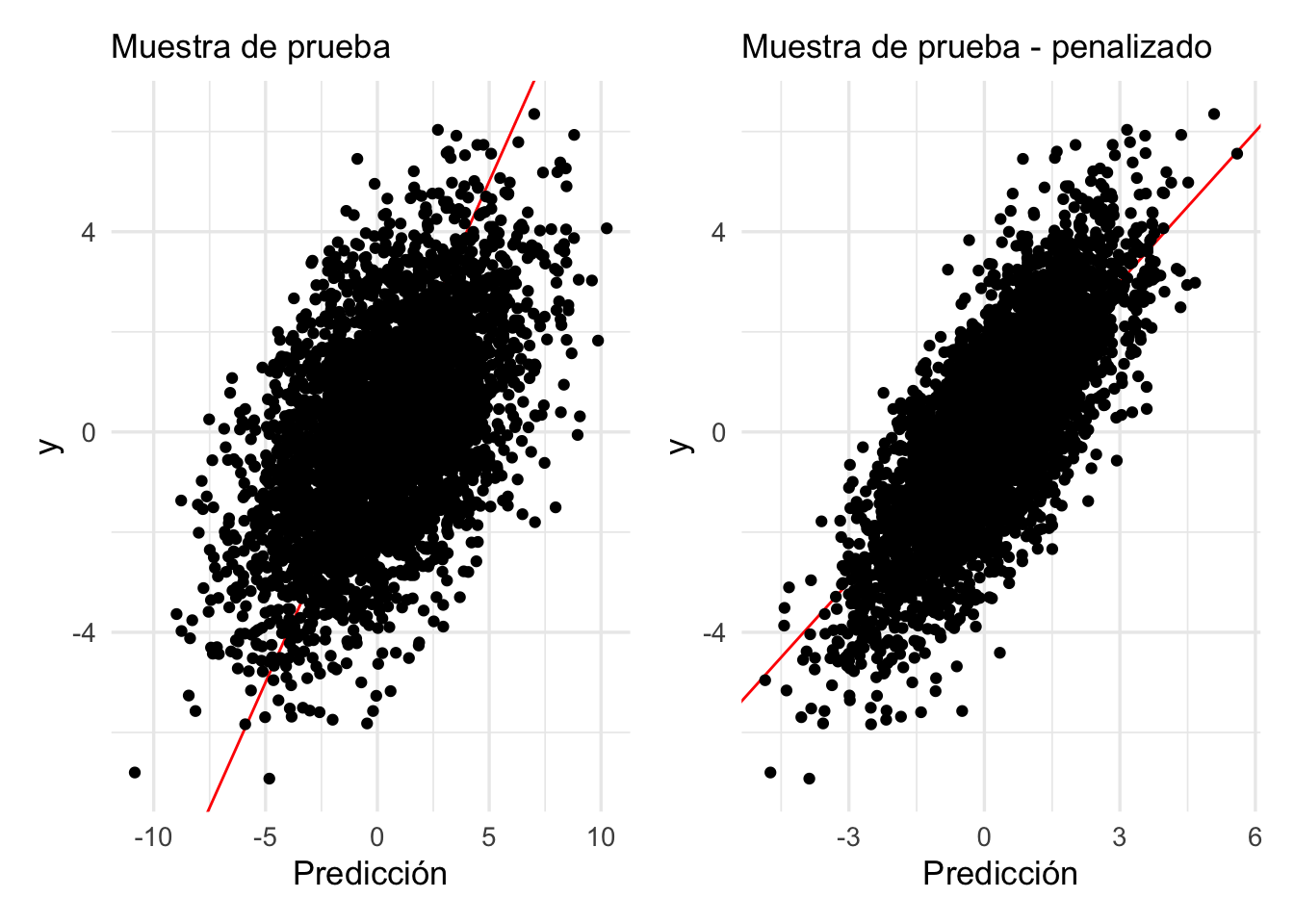
metricas <- metric_set(mae, rmse)
metricas(p_prueba, truth = y, estimate = .pred) |>
mutate(tipo = "no penalizado")## # A tibble: 2 × 4
## .metric .estimator .estimate tipo
## <chr> <chr> <dbl> <chr>
## 1 mae standard 2.06 no penalizado
## 2 rmse standard 2.58 no penalizado
metricas(p_prueba_2, truth = y, estimate = .pred) |>
mutate(tipo = "penalizado")## # A tibble: 2 × 4
## .metric .estimator .estimate tipo
## <chr> <chr> <dbl> <chr>
## 1 mae standard 1.02 penalizado
## 2 rmse standard 1.28 penalizadoY vemos que los errores de predicción se reducen en más de la mitad.
- Obsérvese que esta mejora en varianza tiene un costo: un aumento en el sesgo.
- Sin embargo, lo que nos importa principalmente es reducir el error de predicción, y eso lo logramos escogiendo un balance sesgo-varianza apropiado para los datos y el problema.
6.4 Ejemplo 2: penalización y estimaciones ruidosas
Considéremos los siguientes datos clásicos de Radiación Solar, Temperatura, Velocidad del Viento y Ozono para distintos días en Nueva York (Chambers et al. (1983)):
air_data <- airquality |>
mutate(Wind_cat = cut(Wind, quantile(Wind, c(0, 0.33, 0.66, 1)), include.lowest = T)) |>
filter(!is.na(Ozone) & !is.na(Solar.R))
air <- air_data
ggplot(air, aes(x = Solar.R, y = Ozone, colour = Temp)) + geom_point() +
facet_wrap(~Wind_cat, ncol = 3) +
scale_colour_gradientn(colours = rainbow(2, rev = TRUE))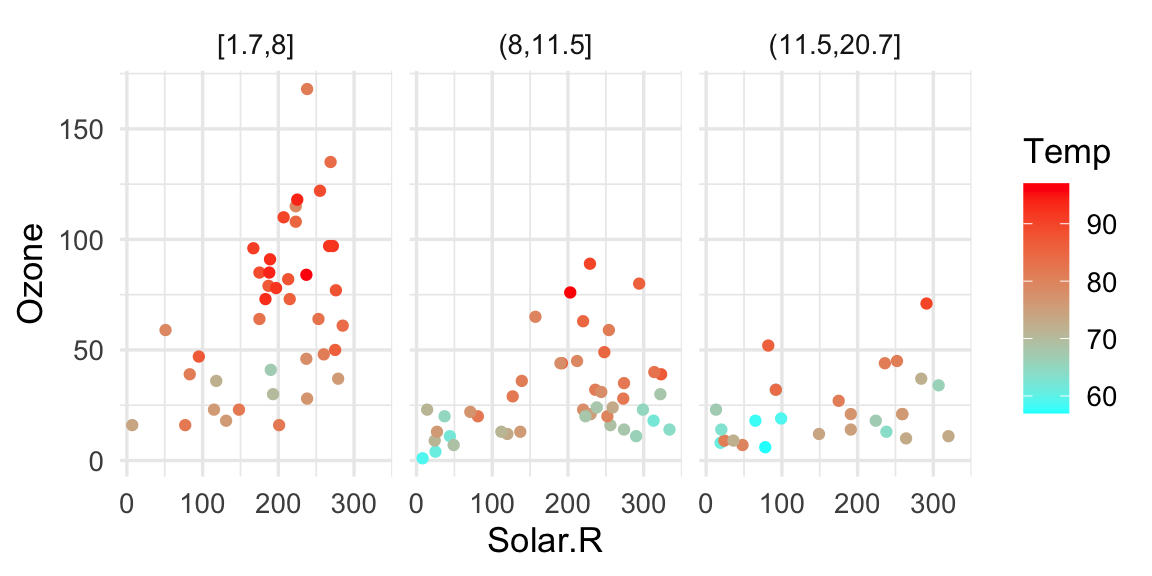 La gráfica muestra algunas interacciones y relaciones no lineales. Formulamos
un modelo lineal como sigue:
La gráfica muestra algunas interacciones y relaciones no lineales. Formulamos
un modelo lineal como sigue:
receta_ozono <- recipe(Ozone ~ Temp + Wind + Solar.R,
data = air) |>
step_poly(Temp, Wind, Solar.R, degree = 2, options = list(raw = TRUE)) |>
step_interact(terms = ~ Temp_poly_1:Wind_poly_1 + Temp_poly_1:Solar.R_poly_1 +
Wind_poly_1:Solar.R_poly_1)
ajuste_ozono <- workflow() |>
add_recipe(receta_ozono) |>
add_model(linear_reg() |> set_engine("lm")) |>
fit(air)Y el ajuste se ve como sigue:
pred_grid <- expand_grid(Wind = c(5,10,15),
Temp = seq(60, 90, 10),
Solar.R = seq(20, 300, by = 10)) |>
mutate(Wind_cat = cut(Wind, quantile(airquality$Wind, c(0, 0.33, 0.66, 1)), include.lowest = T))
pred_grid <- pred_grid |>
bind_cols(predict(ajuste_ozono, pred_grid))
g_lineal <- ggplot(air, aes(x = Solar.R, colour = Temp)) +
geom_point(aes(y = Ozone)) +
facet_wrap( ~ Wind_cat) +
scale_colour_gradientn(colours = rainbow(2, rev = TRUE)) +
geom_line(data = pred_grid, aes(y = .pred, group = interaction(Temp, Wind_cat)), size = 1) +
labs(subtitle = "Curvas de modelo lineal, para viento = 5, 10, 15")
g_lineal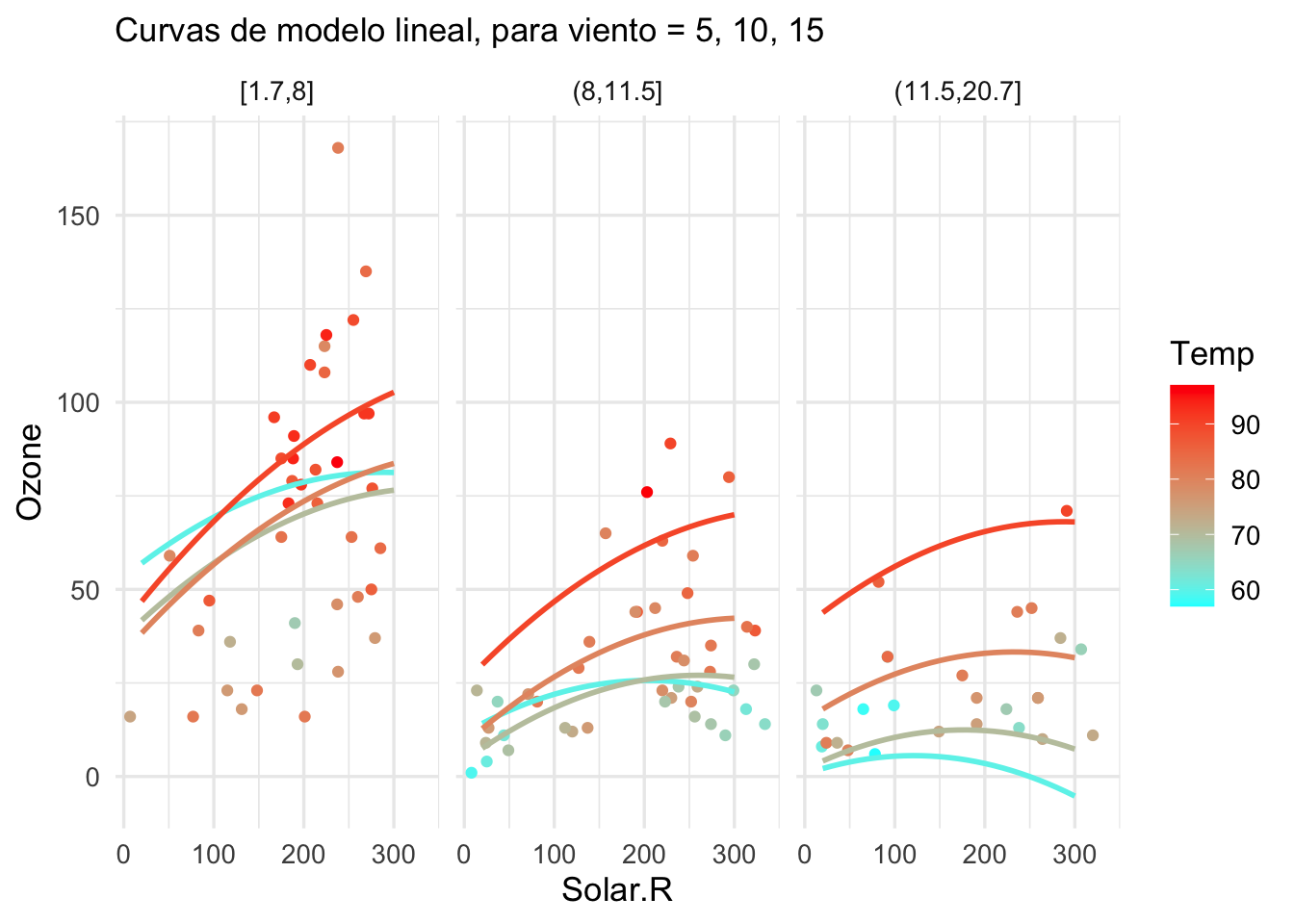
Nótese que algunos aspectos de este modelo parecen ser ruidosos: por ejemplo, el comportamiento de las curvas para el primer pánel (donde hay pocos datos de temperatura baja), el hecho de que en algunos casos parece haber curvaturas decrecientes e incluso predicciones negativas. No deberíamos dar mucho crédito a las predicciones de este modelo, y tiene peligro de producir predicciones desastrosas.
Sin embargo, si usamos algo de regularización:
ajuste_ozono <- workflow() |>
add_recipe(receta_ozono) |>
add_model(linear_reg(mixture = 0, penalty = 0.05) |>
set_engine("glmnet", lambda.min.ratio = 1e-20)) |>
fit(air)
# nota: normalmente no es necesario usar lambda.min.ratioY el ajuste se ve como sigue:
pred_grid <- expand_grid(Wind = c(5,10,15),
Temp = seq(60, 90, 10),
Solar.R = seq(20, 300, by = 10)) |>
mutate(Wind_cat = cut(Wind, quantile(airquality$Wind, c(0, 0.33, 0.66, 1)), include.lowest = T))
pred_grid <- pred_grid |>
bind_cols(predict(ajuste_ozono, pred_grid))
g_lineal <- ggplot(air, aes(x = Solar.R, colour = Temp)) +
geom_point(aes(y = Ozone)) +
facet_wrap( ~ Wind_cat) +
scale_colour_gradientn(colours = rainbow(2, rev = TRUE)) +
geom_line(data = pred_grid, aes(y = .pred, group = interaction(Temp, Wind_cat)), size = 1) +
labs(subtitle = "Curvas de modelo lineal, para viento = 5, 10, 15")
g_lineal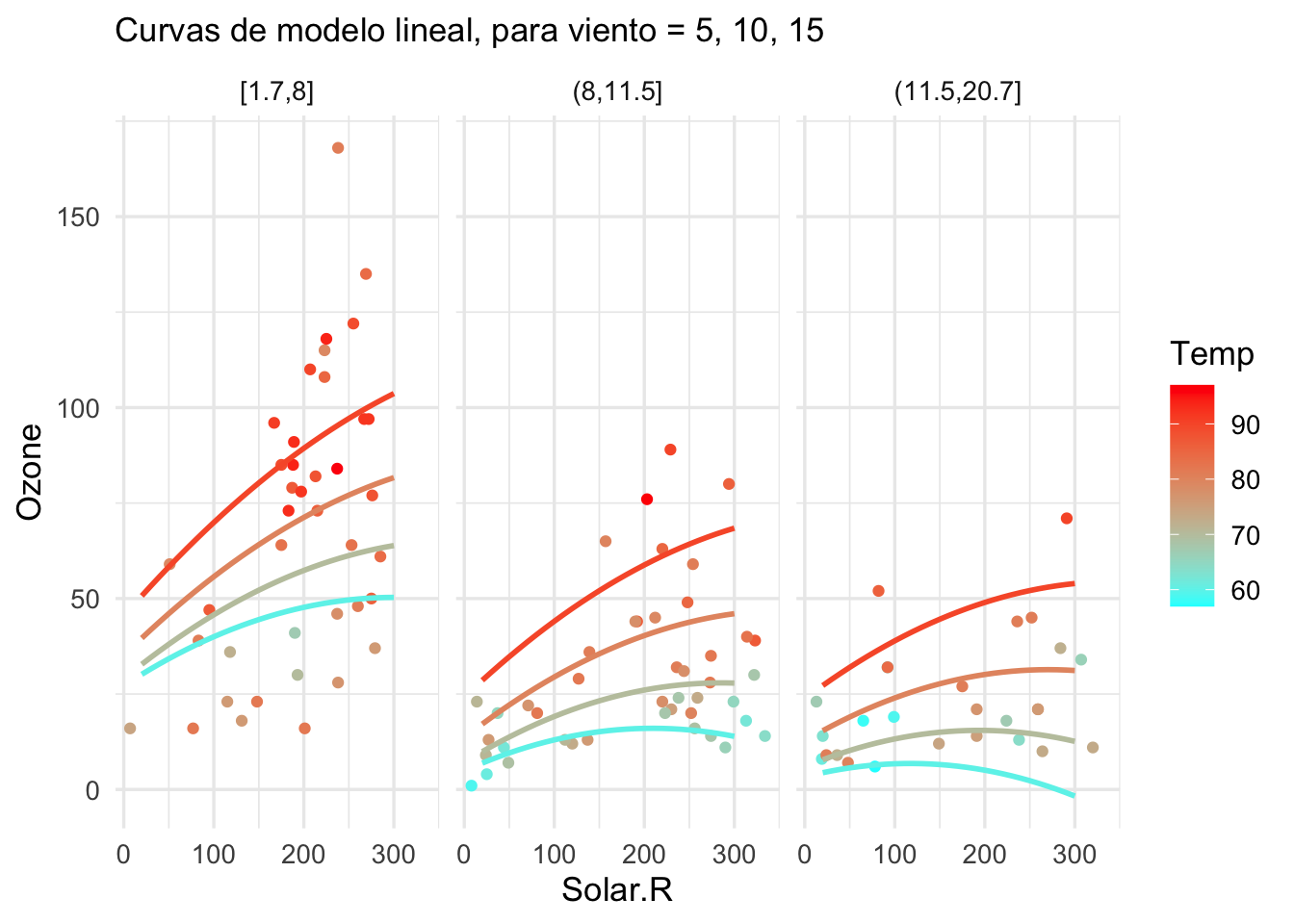
6.5 Regresión ridge: escogiendo el parámetro de complejidad
Como vimos antes, no es posible seleccionar el parámetro \(\lambda\) usando la muestra de entrenamiento (¿con qué \(\lambda\) cómo se obtiene el menor error cuadrático medio sobre la muestra de entrenamiento). Usaremos un conjunto de validación relativamente grande
## Rows: 1460 Columns: 81## ── Column specification ────────────────────────────────────────────────────────
## Delimiter: ","
## chr (43): MSZoning, Street, Alley, LotShape, LandContour, Utilities, LotConf...
## dbl (38): Id, MSSubClass, LotFrontage, LotArea, OverallQual, OverallCond, Ye...##
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.## Rows: 27 Columns: 3## ── Column specification ────────────────────────────────────────────────────────
## Delimiter: ","
## chr (1): Neighborhood
## dbl (2): lat, long##
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.
# esta proporción es para ejemplificar
casas_split <- initial_split(casas, prop = 0.25)
casas_entrena <- training(casas_split)
receta_casas <-
recipe(precio_miles ~ calidad_gral +
area_hab_m2 +
area_garage_m2 + area_sotano_m2 +
area_2o_piso_m2 +
area_lote_m2 +
año_construccion + año_venta +
nombre_zona +
aire_acondicionado + condicion_venta +
condicion_gral + condicion_exteriores + tipo_sotano +
calidad_sotano +
baños_completos +
forma_lote + tipo_edificio + estilo + num_coches +
año_venta,
data = casas_entrena) |>
step_filter(condicion_venta == "Normal") |>
step_select(-condicion_venta, skip = TRUE) |>
step_cut(calidad_gral, breaks = c(3, 5, 7, 8)) |>
step_cut(condicion_gral, breaks = c(3, 5, 7, 8)) |>
step_mutate(sin_piso_2 = as.numeric(area_2o_piso_m2 == 0)) |>
step_unknown(tipo_sotano, calidad_sotano, new_level = "sin sótano") |>
step_other(nombre_zona, threshold = 0.02) |>
step_dummy(calidad_gral, condicion_gral, condicion_exteriores, aire_acondicionado,
tipo_sotano, forma_lote, tipo_edificio, estilo,
nombre_zona, calidad_sotano) |>
step_interact(terms = ~ c(area_hab_m2, area_garage_m2,
area_sotano_m2, area_2o_piso_m2):starts_with("calidad_gral")) |>
step_interact(terms = ~ area_sotano_m2:starts_with("calidad_sotano")) |>
step_interact(terms = ~ c(area_hab_m2, area_garage_m2,
area_sotano_m2, area_2o_piso_m2):starts_with("condicion_gral")) |>
step_interact(terms = ~ c(area_hab_m2, area_garage_m2,
area_sotano_m2, area_2o_piso_m2):starts_with("nombre_zona"))Para ver el número de entradas de este modelo:
prep(receta_casas) |> juice() |> dim()## [1] 289 163
modelo_penalizado <- linear_reg(mixture = 0.0, penalty = tune()) |>
set_engine("glmnet", lambda.min.ratio = 1e-30)
flujo_casas <- workflow() |>
add_recipe(receta_casas) |>
add_model(modelo_penalizado)Construimos los objetos para
# creamos un objeto con datos de entrenamiento y de prueba
val_split <- manual_rset(casas_split |> list(), "validación")
lambda_params <- parameters(penalty(range = c(-3, 3),
trans = log10_trans()))
lambda_grid <- grid_regular(lambda_params, levels = 20)
lambda_grid## # A tibble: 20 × 1
## penalty
## <dbl>
## 1 0.001
## 2 0.00207
## 3 0.00428
## 4 0.00886
## 5 0.0183
## 6 0.0379
## 7 0.0785
## 8 0.162
## 9 0.336
## 10 0.695
## 11 1.44
## 12 2.98
## 13 6.16
## 14 12.7
## 15 26.4
## 16 54.6
## 17 113.
## 18 234.
## 19 483.
## 20 1000
mis_metricas <- metric_set(rmse)
eval_tbl <- tune_grid(flujo_casas,
resamples = val_split,
grid = lambda_grid,
metrics = mis_metricas) ## ! validación: preprocessor 1/1, model 1/1 (predictions): There are new levels in a fac...
ridge_ajustes_tbl <- eval_tbl |>
unnest(cols = c(.metrics)) |>
select(id, penalty, .metric, .estimate)
ridge_ajustes_tbl |> DT::datatable()
ggplot(ridge_ajustes_tbl, aes(x = penalty, y = .estimate, colour = .metric)) +
geom_point() + geom_line() + scale_x_log10() 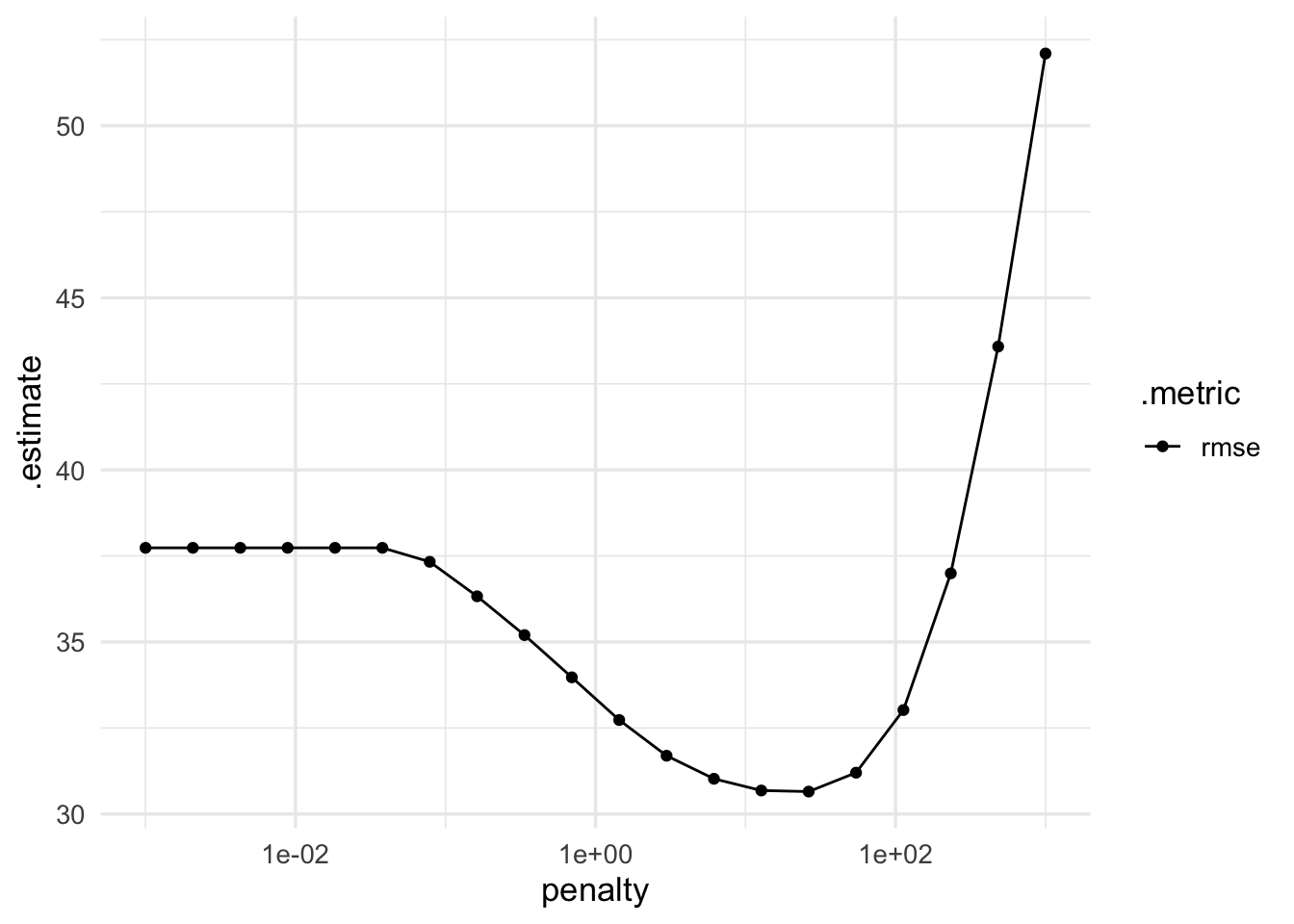
Y vemos que con una penalización alrededor de \(\lambda = 1\) podemos obtener mejor desempeño que con el modelo no regularizado.
Pregunta: en qué partes de la gráfica es relativamente grande la varianza? ¿en qué parte es relativamente grande el sesgo?
6.6 Regresión lasso
Se puede controlar la varianza de mínimos cuadrados de otras maneras. Cuando la varianza proviene también de la inclusión de variables que no necesariamente están relacionadas con la respuesta, podemos usar métodos de selección de variables, como en stepwise regression, por ejemplo.
Otra manera interesante de lograr mejor desempeño predictivo con modelos más parsimoniosos resulta de usar un término de penalización distinto al de ridge. En ridge, el problema que resolvemos es minimizar el objetivo
\[D(a) + \lambda \sum_{j=1}^p a_j^2\]
En regresión lasso, usamos una penalización de tipo \(L_1\):
\[D(a) + \lambda \sum_{j=1}^p |a_j|\] En un principio, no parece ser muy diferente a ridge. Veremos sin embargo que usar esta penalización también se puede ver como un proceso de selección de variables.
6.7 Lasso vs Ridge
Consideramos cómo predecir el porcentaje de grasa corporal a partir de distintas mediciones de dimensiones corporales:
dat_grasa <- read_csv(file = './datos/bodyfat.csv')
set.seed(1832)
grasa_particion <- initial_split(dat_grasa, 0.7)
grasa_ent <- training(grasa_particion)
grasa_pr <- testing(grasa_particion)
# nota: con glmnet no es necesario normalizar, pero aquí lo hacemos
# para ver los coeficientes en términos de las variables estandarizadas:
grasa_receta <- recipe(grasacorp ~ ., grasa_ent) |>
update_role(cadera, cuello, muñeca, tobillo, rodilla, new_role = "ninguno") |>
step_normalize(all_predictors()) |>
prep()
modelo_2 <- linear_reg(mixture = 0, penalty = 0) |>
set_engine("glmnet", lambda.min.ratio = 1e-20)
flujo_2 <- workflow() |>
add_model(modelo_2) |>
add_recipe(grasa_receta)
flujo_2 <- flujo_2 |> fit(grasa_ent)
modelo_2 <- extract_fit_engine(flujo_2)
coefs <- modelo_2 |> tidy() |>
filter(term != "(Intercept)")
ggplot(coefs, aes(x = lambda, y = estimate, colour = term)) +
geom_line(size = 1.4) + scale_x_log10() +
scale_colour_manual(values = cbb_palette) +
labs(subtitle = "Regularizacion L2")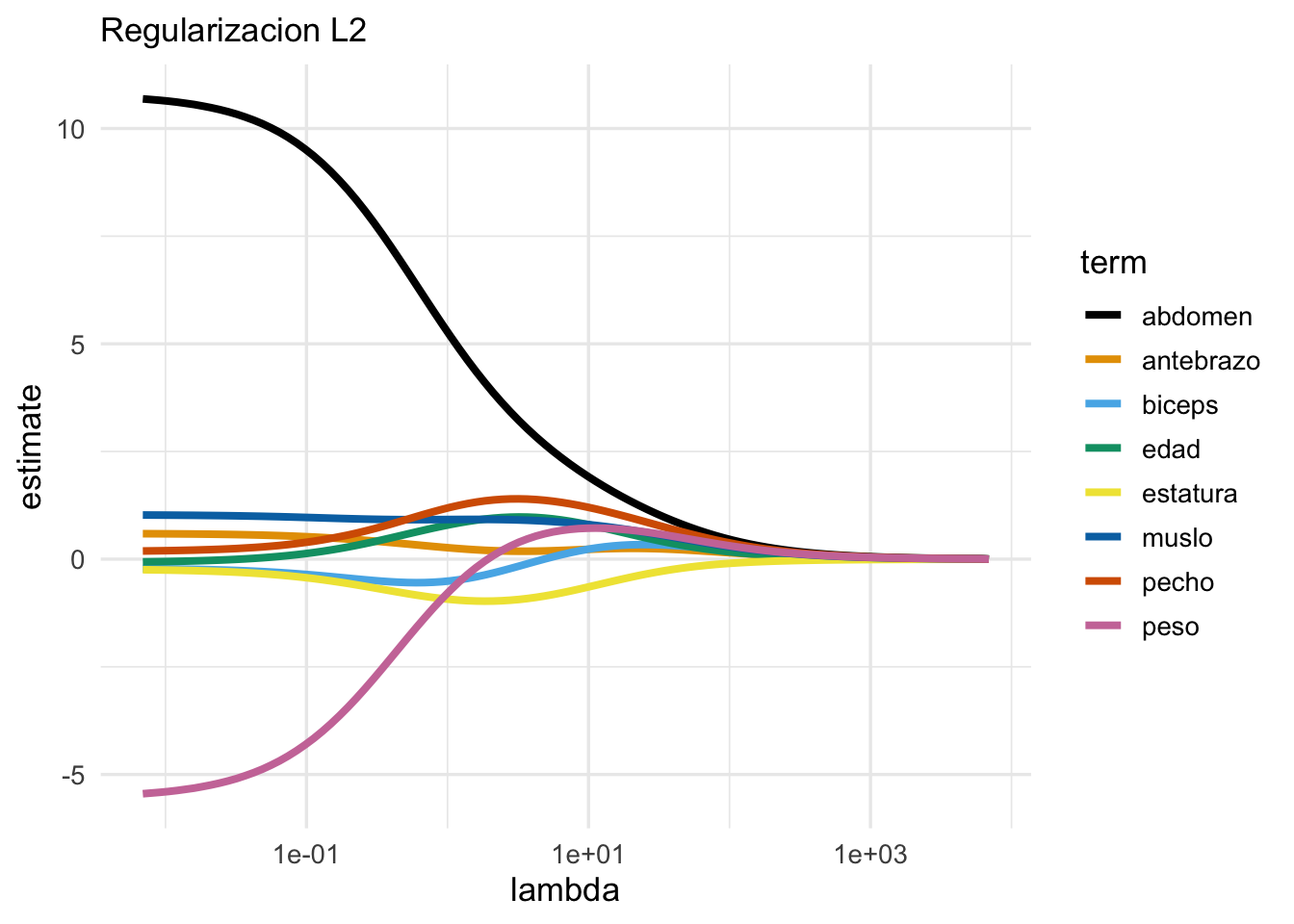
Estas gráfica se llama traza de los coeficientes, y nos muestra cómo cambian los coefi´cientes conforme cambiamos la regularización. Nótese que cuando la regularización es chica, obtenemos algunos resultados contra-intuitivos como que el coeficiente de peso es negativo para predecir el nivel de grasa corporal. Cuando regularizamos más, este coeficiente es positivo. La razón de esto tiene qué ver con la correlación fuerte de las variables de entrada, por ejemplo:
## peso abdomen biceps muslo
## peso 1.00 0.89 0.78 0.86
## abdomen 0.89 1.00 0.65 0.77
## biceps 0.78 0.65 1.00 0.75
## muslo 0.86 0.77 0.75 1.00Ahora probemos con regularización lasso:
## mixture = 1 es regresión lasso
modelo_1 <- linear_reg(mixture = 1, penalty = 0) |>
set_engine("glmnet", lambda.min.ratio = 1e-10)
flujo_1 <- workflow() |>
add_model(modelo_1) |>
add_recipe(grasa_receta)
flujo_1 <- flujo_1 |> fit(grasa_ent)
modelo_1 <- extract_fit_engine(flujo_1)
coefs <- modelo_1 |> tidy() |>
filter(term != "(Intercept)")
ggplot(coefs, aes(x = lambda, y = estimate, colour = term)) +
geom_line(size = 1.4) + scale_x_log10() +
scale_colour_manual(values = cbb_palette) +
labs(subtitle = "Regularizacion L1")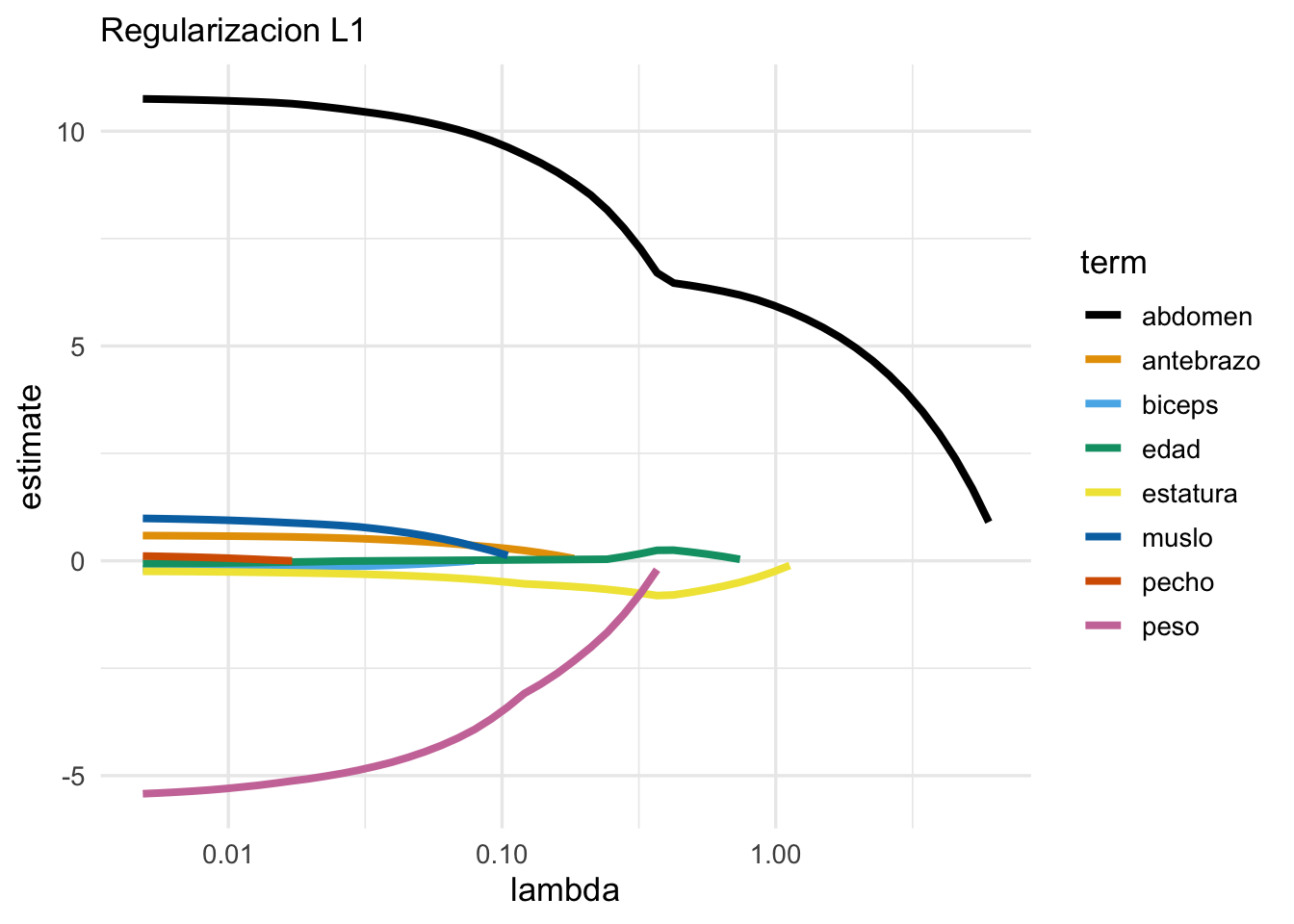 Y nótese que conforme aumentamos la penalización, algunas variables
salen del modelo (sus coeficientes son cero). Por ejemplo, para
un valor de \(lambda\) intermedio, obtenemos un modelo simple de la forma:
Y nótese que conforme aumentamos la penalización, algunas variables
salen del modelo (sus coeficientes son cero). Por ejemplo, para
un valor de \(lambda\) intermedio, obtenemos un modelo simple de la forma:
## # A tibble: 3 × 3
## term estimate lambda
## <chr> <dbl> <dbl>
## 1 edad 0.248 0.424
## 2 estatura -0.795 0.424
## 3 abdomen 6.46 0.424Y nótese que este modelo solo incluye 3 variables.La traza confirma que la regularización lasso, además de encoger coeficientes, saca variables del modelo conforme el valor de regularización aumenta.
La razón de esta diferencia cualitativa entre cómo funciona lasso y ridge se puede entender considerando que los problemas de penalización mostrados arriba puede escribirse en forma de problemas de restricción. Por ejemplo, lasso se puede reescribir como el problema de resolver
\[\min_a D(a)\] sujeto a \[\sum_{i=1}^p a_j^2 < t\] En la gráfica siguiente (tomada de Hastie, Tibshirani, and Friedman (2017)), lasso está a la izquierda y ridge está a la derecha, las curvas rojas son curvas de nivel de la suma de cuadrados \(D(a)\), y \(\hat{beta}\) es el estimador usual de mínimos cuadrados de los coeficientes (sin penalizar). En azul está la restricción:
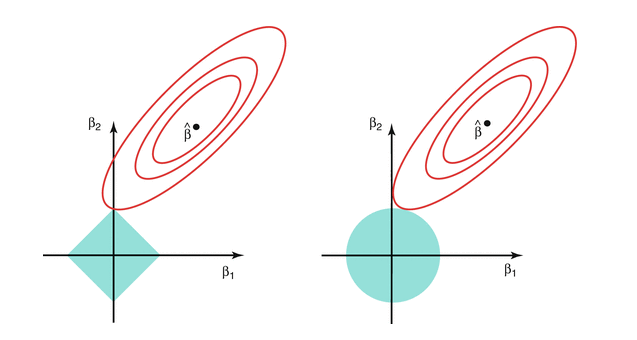
Ridge vs Lasso
En regresión ridge, los coeficientes se encogen gradualmente desde la solución no restringida hasta el origen. Ridge es un método de encogimiento de coeficientes. Regresión ridge es especialmente útil cuando tenemos varias variables de entrada fuertemente correlacionadas. Regresión ridge intenta encoger juntos coeficientes de variables correlacionadas para reducir varianza en las predicciones.
En regresión lasso, los coeficientes se encogen gradualmente, pero también se excluyen variables del modelo. Por eso lasso es un método de encogimiento y selección de variables. Lasso encoge igualmente coeficientes para reducir varianza, pero también comparte similitudes con regresión de mejor subconjunto, en donde para cada número de variables \(l\) buscamos escoger las \(l\) variables que den el mejor modelo. Sin embargo, el enfoque de lasso es más escalable y puede calcularse de manera más simple.
Nota: es posible también utilizar una penalización que mezcla ridge y lasso:
\[\lambda \left (\alpha \sum_j |a_j| + (1-\alpha)\sum_j a_j^2 \right )\]
y \(\alpha\) es un parámetro que podemos afinar:
# elastic net = ridge + lasso
# mixture es alpha y penalty es lambda
modelo_enet <- linear_reg(mixture = 0.5, penalty = 0.05)
# y si queremos afinar:
modelo_enet <- linear_reg(mixture = tune(), penalty = tune())