Skip to main content

Introducción a Machine Learning con R

11 Redes neuronales

11.1 Introducción a redes neuronales

En partes anteriores, vimos cómo hacer más flexibles los métodos de regresión: la idea es construir entradas derivadas a partir de las variables originales, e incluirlas en el modelo de regresión. Este enfoque es bueno cuando tenemos relativamente pocas variables originales de entrada, y tenemos una idea de qué variables derivadas es buena idea incluir (por ejemplo interacciones para variables importantes). Sin embargo, si hay una gran cantidad de entradas, esta técnica puede ser prohibitiva en términos de cálculo y trabajo manual.

Por ejemplo, si tenemos unas 100 entradas numéricas, al crear todas las interacciones \(x_i x_j\) y los cuadrados \(x_i^2\) terminamos con unas 5150 variables. Para el problema de dígitos (256 entradas o pixeles) terminaríamos con unas 32 mil entradas adicionales. Aún cuando es posible regularizar, en estos casos suena más conveniente construir entradas derivadas a partir de los datos.

Para hacer esto, consideramos entradas \(X_1, . . . , X_p\), y supongamos que tenemos un problema de regresión con respuesta \(Y\). Aunque hay muchas maneras de construir entradas derivadas, una manera simple sería construir \(m\) nuevas entradas mediante:

\[a_k = h \left ( \theta_{k,0} + \sum_{j=1}^p \theta_{k,j}x_j \right)\]

para \(k=1,\ldots, m\), donde \(h\) es la función logística, y las \(\theta\) son parámetros que seleccionaremos más tarde. La idea es hacer combinaciones lineales de variables transformadas.

Recordamos que:

La función logística está dada por \[h(x)=\frac{e^x}{1+e^x}\]

cuya gráfica es:

h <- function(x){exp(x)/(1+exp(x)) }
ggplot(tibble(x = seq(-6, 6, 0.01)), aes(x = x)) + stat_function(fun = h)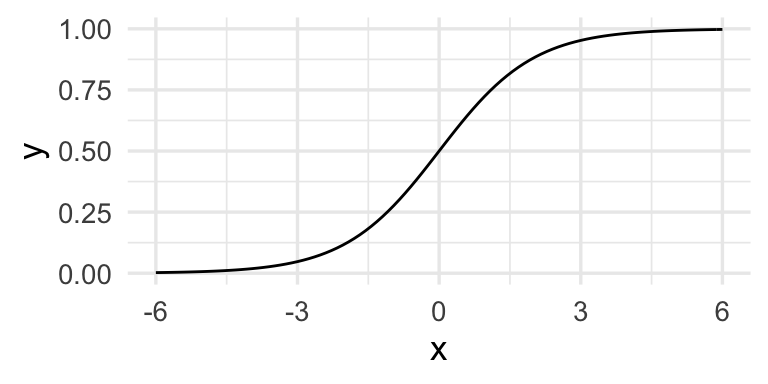

Nótese que esta función no lineal hacer combinaciones lineales de las variables originales que de alguna forma se encienden o apagan dependiendo de los valores de esas combinaciones lineales.

Buscamos hacer predicciones mediante un modelo lineal, pero en lugar de usar las entradas originales X usamos las entradas derivadas \(a_1, . . . , a_m\): \[f(x) = \beta_0 + \sum_{j=1}^m \beta_ja_j\]

Podemos representar este esquema con una red dirigida (\(m=3\) variables derivadas):

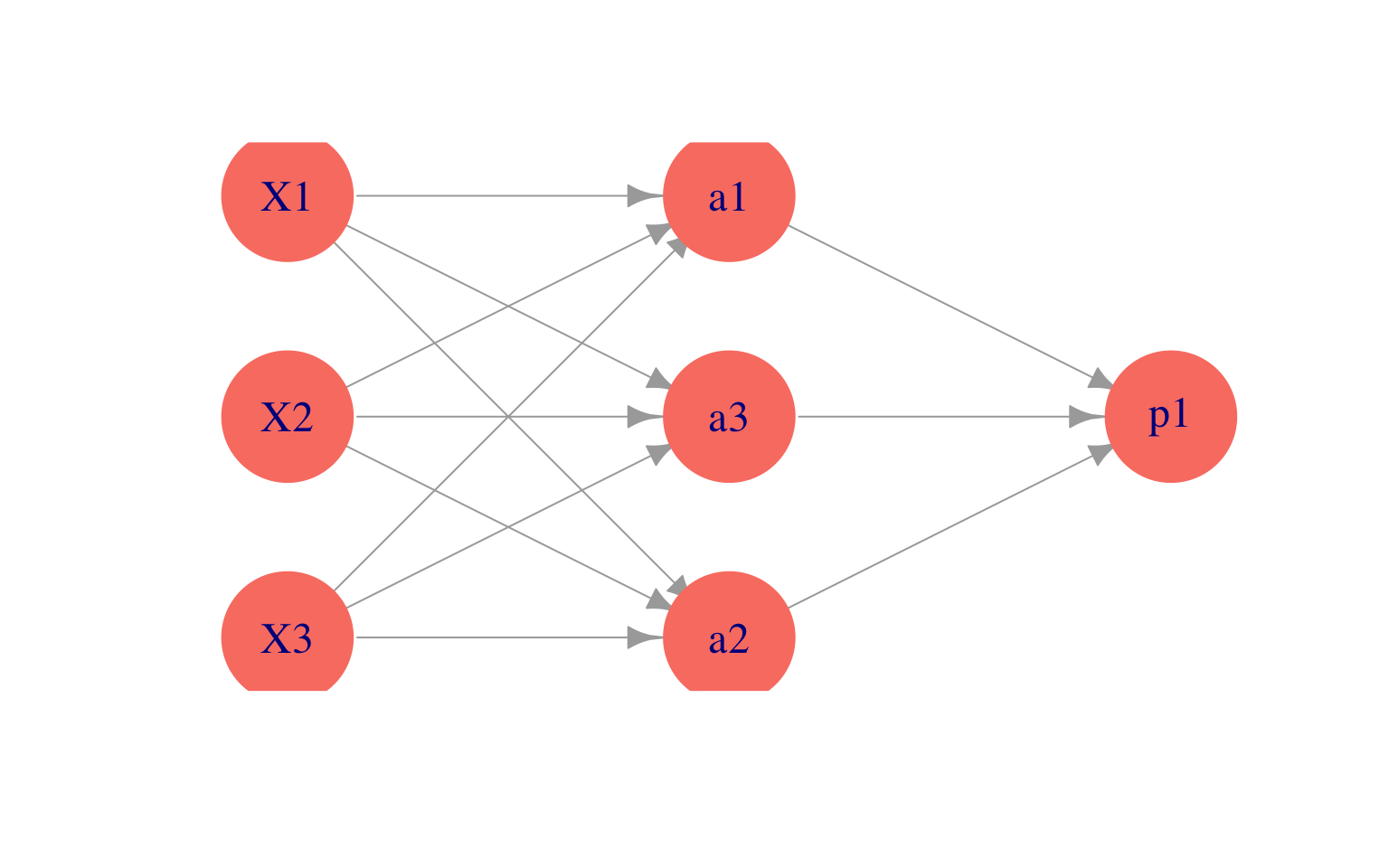
Observaciones:

  • ¿Por qué usar \(h\) para las entradas derivadas \(a_k\)? En primer lugar, nótese que si no transformamos con alguna función no lineal \(h\), el modelo final \(f(x)\) para la probabilidad condicional es el mismo que el de regresión lineal (combinaciones lineales de combinaciones lineales son combinaciones lineales). Sin embargo, al transformar con \(h\), las \(x_j\) contribuyen de manera no lineal a las entradas derivadas.
  • Es posible demostrar que si se crean suficientes entradas derivadas (\(m\) es suficientemente grande), entonces la función \(f(x)\) puede aproximar cualquier función continua. La función \(h\) (que se llama función de activación no es especial: funciones continuas con forma similar a la sigmoide (logística) pueden usarse también (por ejemplo, arcotangente, o lineal rectificada). La idea es que cualquier función se puede aproximar mediante superposición de funciones tipo sigmoide (ver por ejemplo Cybenko 1989, Approximation by Superpositions of a Sigmoidal Function).

11.2 ¿Cómo construyen entradas las redes neuronales?

Comencemos por un ejemplo simple de clasificación binaria con una sola entrada \(x\). Supondremos que el modelo verdadero está dado por:

h <- function(x){
    1/(1 + exp(-x)) # es lo mismo que exp(x)/(1 + exp(x))
}
x <- seq(-2, 2, 0.01)
f <- atan(2 - 3 * x^2) 
set.seed(2851)
x_1 <- runif(20, -2, 2)
y_1 <- rnorm(20, atan(2 - 3 * x_1^2), 0.5)
datos <- data.frame(x_1, y_1)
dat_p <- data.frame(x, f)
g <- qplot(x, f, geom='line')
g + geom_point(data = datos, aes(x = x_1, y = y_1), colour = 'red')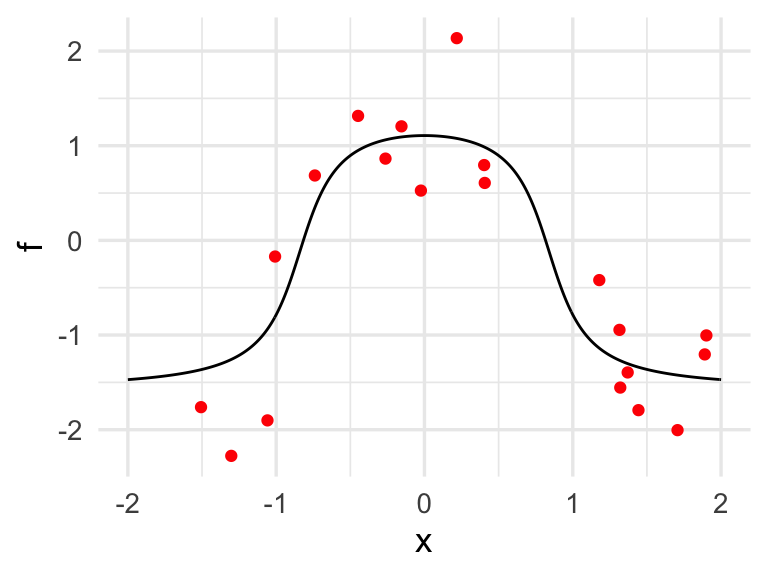

donde adicionalmente graficamos 30 datos simulados.
Recordamos que queremos ajustar la curva negra. Podríamos ajustar un modelo de regresión expandiendo manualmente el espacio de entradas agregando \(x^2\) y quizá otros términos, y obtendríamos un ajuste razonable. Pero la idea aquí es que podemos crear entradas derivadas de forma automática.

Supongamos entonces que pensamos crear dos entradas \(a_1\) y \(a_2\), funciones de \(x_1\), y luego predecir \(y\) en función de estas dos entradas. Por ejemplo, podríamos tomar:

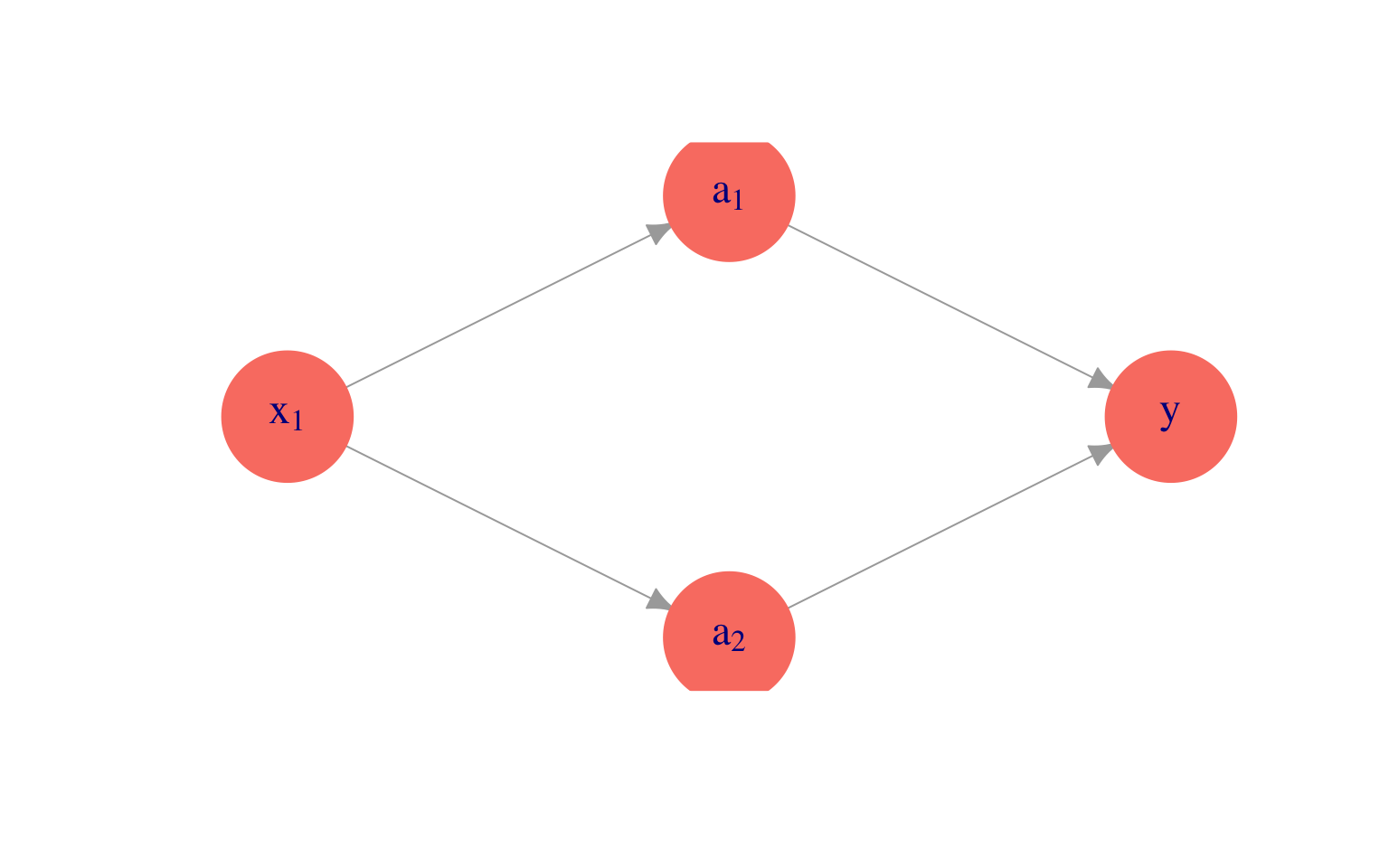
donde hacemos una regresión lineal para predecir \(y\) mediante \[f(a) = \beta_0 + \beta_1a_1+\beta_2 a_2,\] \(a_1\) y \(a_2\) están dadas por \[a_1(x)=h(\beta_{1,0} + \beta_{1,1} x_1),\] \[a_2(x)=h(\beta_{2,0} + \beta_{2,1} x_1).\]

Por ejemplo, podríamos tomar

a_1 <- h( -6 - 6 * x)  # -6(x + 1/6)
a_2 <- h(6 - 6 * x)  # -6(x - 1/6) # una es una versión desplazada de otra.

Las funciones \(a_1\) y \(a_2\) dependen de \(x\) de la siguiente forma:

dat_a <- tibble(x = x, a_1 = a_1, a_2 = a_2)
dat_a |> pivot_longer(a_1:a_2, names_to = "variable", values_to = "valor") |> 
ggplot(aes(x=x, y=valor, colour=variable, group=variable)) + geom_line()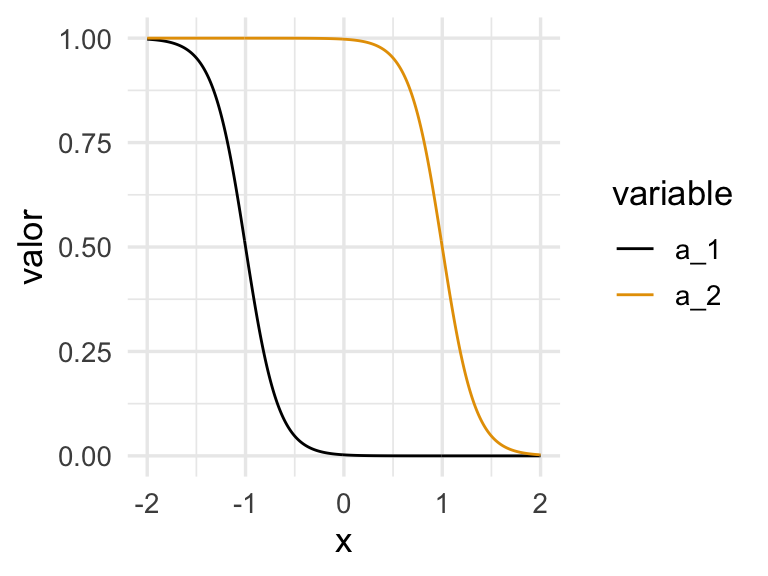

Si las escalamos y sumamos, obtenemos

dat_a <- dat_a |>  
  mutate(suma =  -  a_1 +  a_2)
dat_a_2 <- dat_a |> pivot_longer(a_1:suma, names_to = "variable", values_to = "valor")
ggplot(dat_a_2, aes(x = x, y = valor, colour = variable, group = variable)) + geom_line()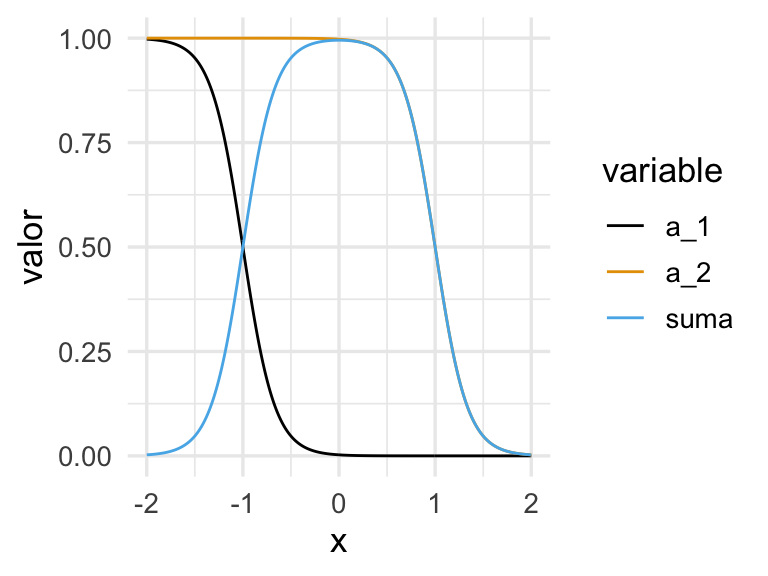

y finalmente calculamos la salida:

dat_2 <- tibble(x, y = (-1 - 2 * a_1 + 2 * a_2))
ggplot(dat_2, aes(x = x, y = y)) + geom_line()+
geom_line(data=dat_p, aes(x = x,y = f), col = "red") + 
   geom_point(data = datos, aes(x = x_1, y = y_1))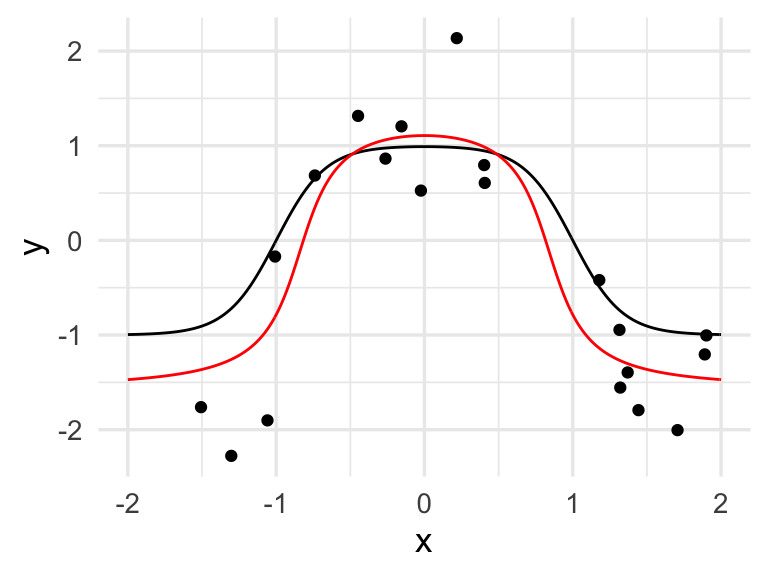

que da un ajuste razonable. Este es un ejemplo de cómo la mezcla de dos funciones logísticas puede replicar esta función con forma de chipote.

11.3 ¿Cómo ajustar los parámetros?

Para encontrar los mejores parámetros, minimizamos el error de entrenamiento (que llamaremos también devianza de entrenamiento) sobre los parámetros \(\beta_0,\beta_1,\beta_2\) y \(\beta_{1,0},\beta_{1,1},\beta_{2,0},\beta_{2,1}\).

Veremos más adelante que conviene hacer esto usando descenso o en gradiente o descenso en gradiente estocástico, pero por el momento usamos la función optim de R para minimizar la devianza. En primer lugar, creamos una función que para todas las entradas calcula los valores de salida. En esta función hacemos feed-forward de las entradas a través de la red para calcular la salida.

## esta función calcula los valores de cada nodo en toda la red,
## para cada entrada
feed_fow <- function(beta, x){
  a_1 <- h(beta[1] + beta[2] * x) # calcula variable 1 de capa oculta
  a_2 <- h(beta[3] + beta[4] * x) # calcula variable 2 de capa oculta
  y <- (beta[5] + beta[6] * a_1 + beta[7] * a_2) # calcula capa de salida
  y
}

Nótese que simplemente seguimos el diagrama mostrado arriba para hacer los cálculos, combinando linealmente las entradas en cada capa.

Ahora definimos una función para calcular la devianza. Conviene crear una función que crea funciones, para obtener una función que sólo se evalúa en los parámetros para cada conjunto de datos de entrenamiento fijos:

devianza_fun <- function(x, y){
    # esta función es una fábrica de funciones
   devianza <- function(beta){
         f <- feed_fow(beta, x)
         mean((y - f)^2)
   }
  devianza
}

Por ejemplo:

dev <- devianza_fun(x_1, y_1) # crea función dev
## ahora dev toma solamente los 7 parámetros beta:
dev(c(0,0,0,0,0,0,0))
## [1] 1.864901

Finalmente, optimizamos la devianza. Para esto usaremos la función optim de R:

set.seed(15)
salida <- optim(rnorm(7), dev, method = 'BFGS',
                control = list(maxit = 5000)) # inicializar al azar punto inicial
beta <- salida$par
beta
## [1] -18.504149  15.924226  61.110606  60.234770  -2.043403  -2.506113   3.060480

Y ahora podemos graficar con el vector \(\beta\) encontrado:

## hacer feed forward con beta encontrados
p_2 <- feed_fow(beta, x)
dat_2 <- data.frame(x, p_2 = p_2)
ggplot(dat_2, aes(x = x, y = p_2)) + geom_line()+
geom_line(data = dat_p, aes(x = x, y = f), col='red') +
   geom_point(data = datos, aes(x = x_1, y = y_1))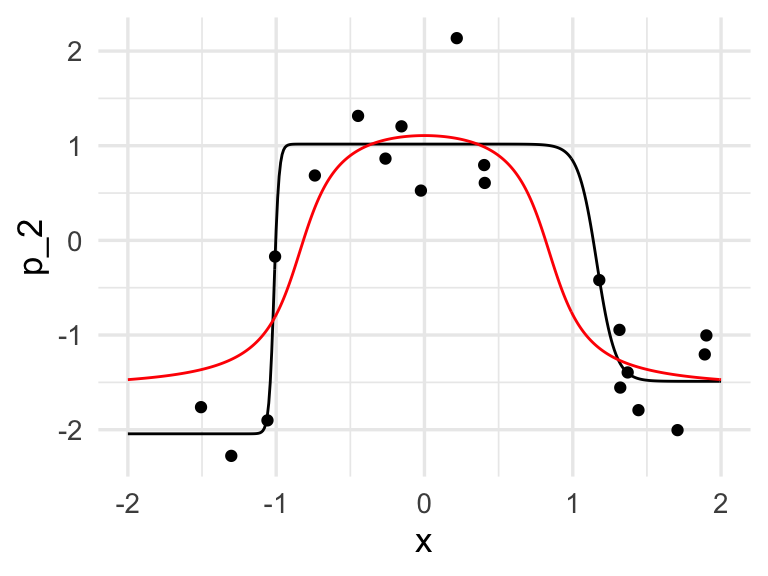

Los coeficientes estimados, que en este caso muchas veces se llaman pesos, son:

beta |> round(2)
## [1] -18.50  15.92  61.11  60.23  -2.04  -2.51   3.06

que parecen ser muy grandes. Igualmente, de la figura vemos que el ajuste no parece ser muy estable (esto se puede confirmar corriendo con distintos conjuntos de entrenamiento). Podemos entonces regularizar ligeramente la devianza para resolver este problema. En primer lugar, definimos la devianza regularizada (ridge), donde penalizamos todos los coeficientes que multiplican a una variable, pero no los intercepts:

devianza_reg <- function(x, y, lambda){
    # esta función es una fábrica de funciones
   devianza <- function(beta){
         f <- feed_fow(beta, x)
         # en esta regularizacion quitamos sesgos, pero puede hacerse también con sesgos.
         sum((y-f)^2)  + lambda * sum(beta[-c(1,3,5)]^2) 
   }
  devianza
}
dev_r <- devianza_reg(x_1, y_1, 0.01) # crea función dev
set.seed(5)
salida <- optim(rnorm(7), dev_r, method='BFGS') # inicializar al azar punto inicial
beta <- salida$par
dev(beta)
## [1] 0.2234812
y_2 <- feed_fow(beta, x)
dat_2 <- data.frame(x, y_2 = y_2)
ggplot(dat_2, aes(x = x, y = y_2)) + geom_line()+
geom_line(data = dat_p, aes(x = x, y = f), col='red') +
   geom_point(data = datos, aes(x = x_1, y = y_1))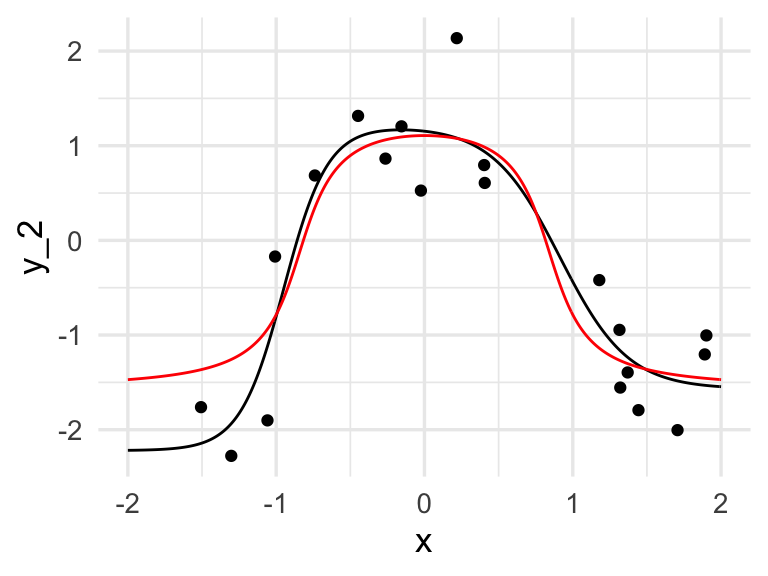

y obtenemos un ajuste mucho más estable. Podemos usar también keras. El modelo, con una capa intermedia de dos unidades, y regularización ridge para los coeficientes, y optimización por descenso en gradiente se define como:

reticulate::use_virtualenv("~/tensorflow-metal/", required = TRUE)
library(keras)
# construir modelo
ejemplo_mod <- keras_model_sequential()
ejemplo_mod |> 
   layer_dense(units = 2, 
    activation = "sigmoid", kernel_regularizer = regularizer_l2(0.0005)) |> 
  layer_dense(units = 1, 
    activation = "linear", kernel_regularizer = regularizer_l2(0.0005))
x_mat <- as.matrix(datos$x_1, ncol = 1)
y <- datos$y_1
# usamos devianza como medida de error y descenso en gradiente:
ejemplo_mod |> compile(loss = "mse", 
  optimizer = optimizer_sgd(learning_rate = 0.3))
# nota: esta learning rate (lr) es demasiado alta para problemas típicos
historia <- ejemplo_mod |> 
  fit(x_mat, y, 
      batch_size = nrow(x_mat), epochs = 1000, verbose = 0)

Después de verificar convergencia (chécalo examinando la variable historia), graficamos para ver que obtuvimos resultados similares:

p_3 <- predict(ejemplo_mod, as.matrix(x, ncol = 1))
dat_3 <- tibble(x = x, p_2 = p_3)
ggplot(dat_3, aes(x = x, y = p_2)) + geom_line()+
geom_line(data = dat_p, aes(x = x, y = f), col='red') +
   geom_point(data = datos, aes(x = x_1, y = y_1))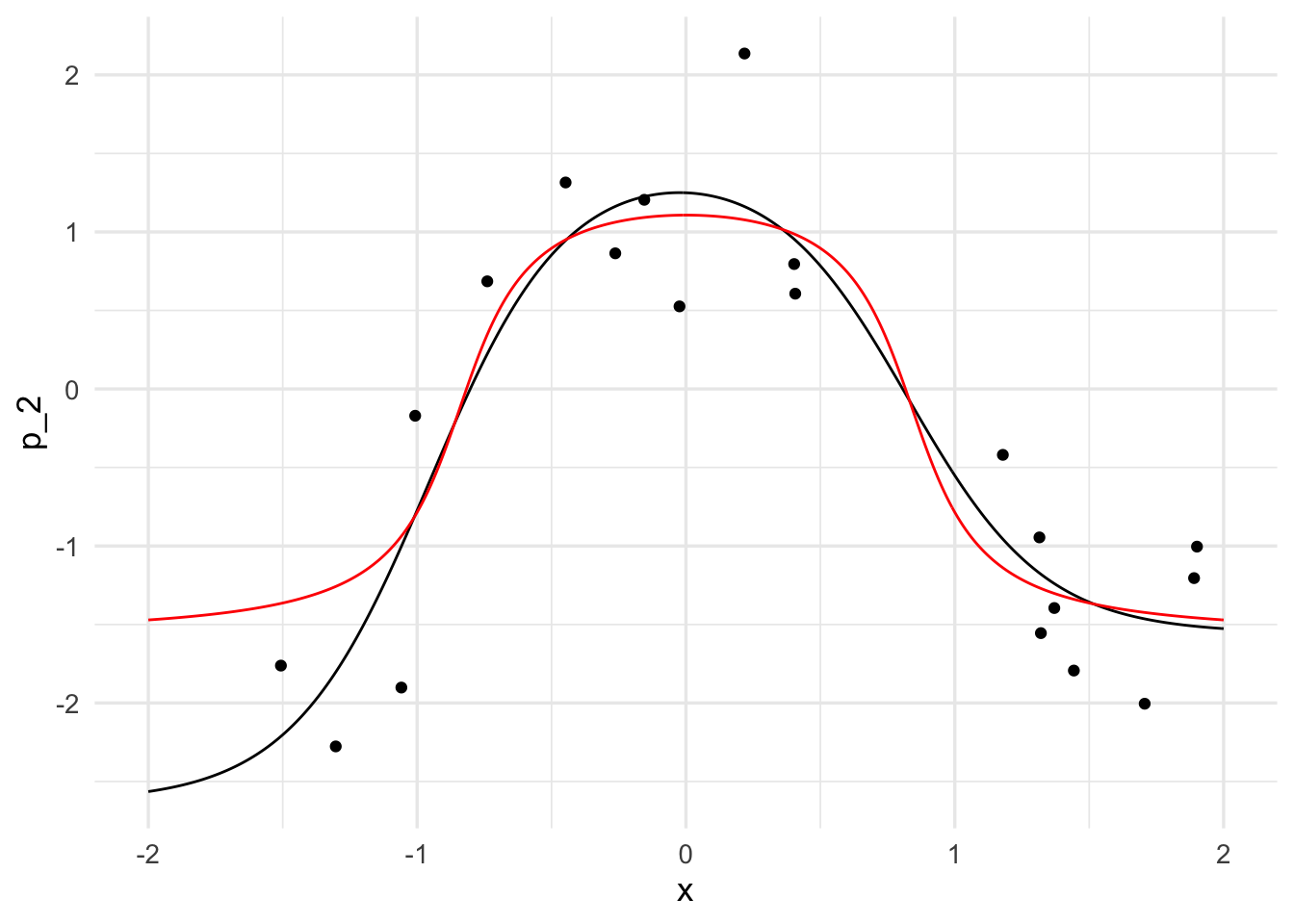

Los coeficientes obtenidos están abajo. Nótese: la primera componente de la lista son los coeficientes de la unidad 1 y 2 para \(x\). La segunda son los sesgos u ordenadas al origen, la tercera los coeficientes de la respuesta para las unidades 1 y 2, y el cuarto es el sesgo u ordenada al origen de la unidad de salida:

get_weights(ejemplo_mod)
## [[1]]
##           [,1]      [,2]
## [1,] -3.931292 -3.922101
## 
## [[2]]
## [1] -3.750576  3.232494
## 
## [[3]]
##           [,1]
## [1,] -4.087585
## [2,]  3.013547
## 
## [[4]]
## [1] -1.555906

Ejercicio: compara los coeficientes que obtuviste en este ejemplo con los anteriores.

11.4 Interacciones en redes neuronales

Es posible capturar interacciones con redes neuronales. Consideremos el siguiente ejemplo simple:

f <- function(x1, x2){
  ( 10*(2 * x1 - 1)*(2 * x2 - 1))
}
dat <- expand.grid(x1 = seq(0, 1, 0.05), x2 = seq(0, 1, 0.05))
dat <- dat |> mutate(f = f(x1, x2))
ggplot(dat, aes(x=x1, y=x2)) + geom_tile(aes(fill=f))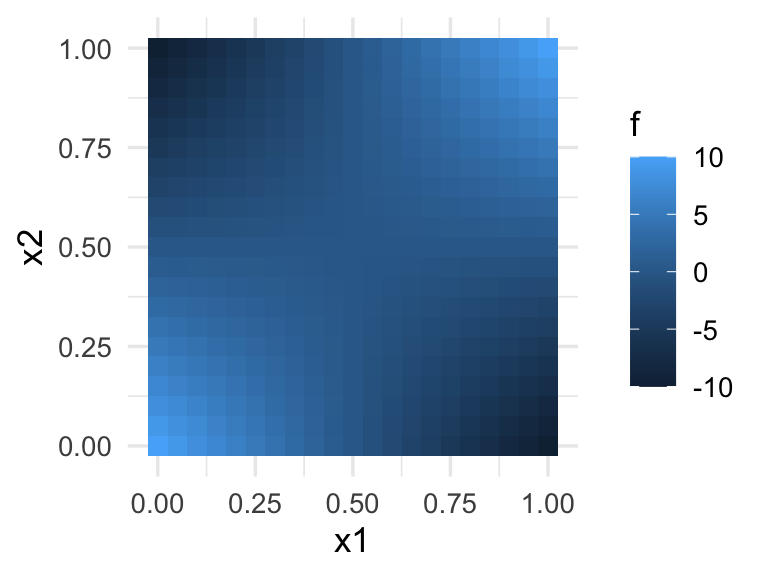

Esta función puede entenderse como un o exclusivo: la probabilidad es alta sólo cuando \(x_1\) y \(x_2\) tienen valores opuestos (\(x_1\) grande pero \(x_2\) chica y viceversa).

No es posible modelar esta función mediante el modelo lineal (sin interacciones). Pero podemos incluir la interacción en el modelo lineal o intentar usar una red neuronal. Primero simulamos unos datos y probamos el modelo lineal con y sin interacciones:

set.seed(322)
n <- 1000
dat_ent <- tibble(x1 = runif(n,0,1), x2 = runif(n, 0, 1)) |>
  mutate(f = f(x1, x2)) |>
  mutate(y = rnorm(n, f, 1))
mod_1 <- lm(y ~ x1 + x2, data = dat_ent)
mod_1
## 
## Call:
## lm(formula = y ~ x1 + x2, data = dat_ent)
## 
## Coefficients:
## (Intercept)           x1           x2  
##    -0.18119      0.08726      0.16049

El resultado del modelo lineal es malo:

qplot(predict(mod_1) , dat_ent$y)

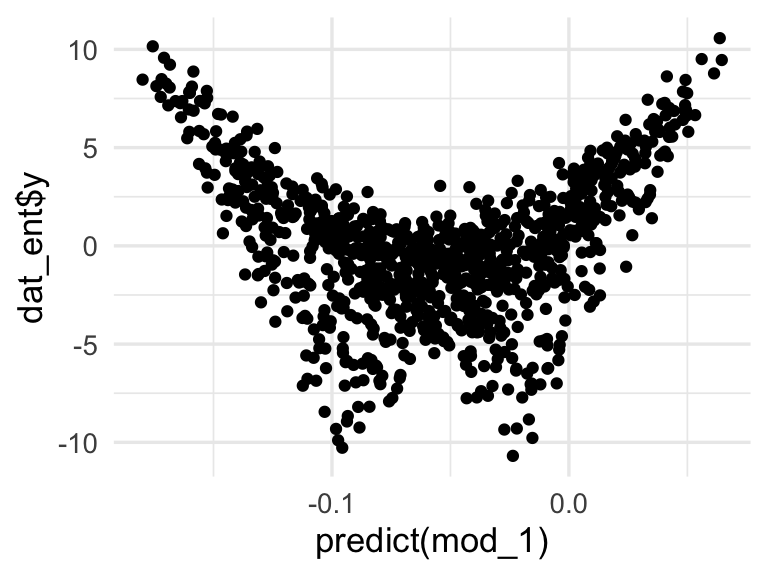
Sin embargo, agregando una interacción lo mejoramos considerablemente (examina la devianza y el error de clasificación):

mod_2 <- lm(y ~ x1 + x2 + x1:x2, data = dat_ent)
mod_2
## 
## Call:
## lm(formula = y ~ x1 + x2 + x1:x2, data = dat_ent)
## 
## Coefficients:
## (Intercept)           x1           x2        x1:x2  
##       9.969      -19.980      -20.005       40.126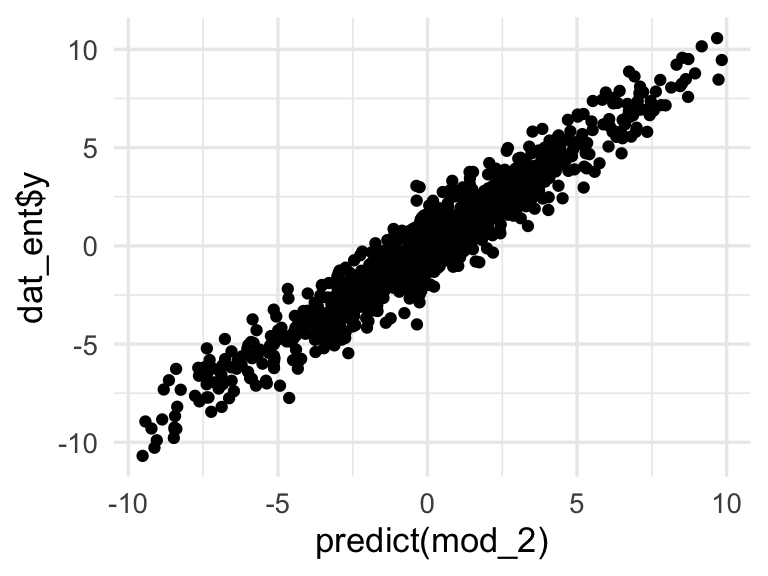
qplot(predict(mod_2), dat_ent$y)

Obsérvese la gran diferencia de devianza entre los dos modelos (en este caso, el sobreajuste no es un problema).

Ahora consideramos qué red neuronal puede ser apropiada.

reg <- regularizer_l2(0.001)
mod_inter <- keras_model_sequential()
mod_inter |> 
  layer_dense(input_shape = 2, units = 4, 
              kernel_regularizer = reg, activation = "sigmoid",
              name = "capa_intermedia") |>
  layer_dense(units = 1, kernel_regularizer = reg, name = "capa_final", activation = "linear")
mod_inter |> compile(loss = "mse", 
  optimizer = optimizer_sgd(learning_rate = 0.2))
historia <- mod_inter |> 
  fit(dat_ent |> select(x1, x2) |> as.matrix(), dat_ent$y, 
      batch_size = 50, epochs = 100, verbose = 0)

Verificamos que esta red captura la interacción:

preds <- predict(mod_inter, dat |> select(x1, x2) |> as.matrix())
dat <- dat |> mutate(p_red = preds)
ggplot(dat, aes(x=x1, y=x2)) + geom_tile(aes(fill = p_red))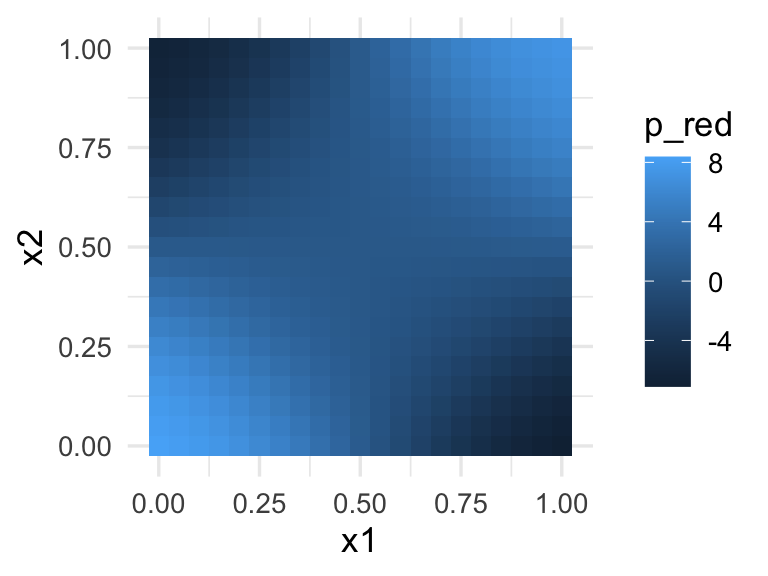

Aunque podemos extraer los cálculos de la red ajustada, vamos a hacer el cálculo de la red a mano. La función feed forward es:

beta <- get_weights(mod_inter)
feed_fow <- function(beta, x){
  a <- h(t(beta[[1]]) %*% x + as.matrix(beta[[2]], 2, 1)) 
  f <- t(beta[[3]]) %*% a + as.matrix(beta[[4]], 1, 1)
  f
}

Observación: ¿cómo funciona esta red? Consideremos la capa intermedia (3 unidades) para cuatro casos: \((0,0), (0,1), (1,0), (1,1)\):

mat_entrada <- tibble(x_1 = c(0,0,1,1), x_2 = c(0,1,0,1)) |> as.matrix()
capa_1 <- keras_model(inputs = mod_inter$input,
    outputs = get_layer(mod_inter, "capa_intermedia")$output)
predict(capa_1, mat_entrada) |> round(2)
##      [,1] [,2] [,3] [,4]
## [1,] 0.02 0.98 1.00 0.92
## [2,] 0.91 1.00 0.97 0.02
## [3,] 0.00 0.16 0.97 0.03
## [4,] 0.02 0.98 0.08 0.00

Y los pesos para calcular esta capa son:

beta[1:2] 
## [[1]]
##           [,1]      [,2]      [,3]      [,4]
## [1,] -6.508098 -5.467762 -5.892983 -6.090854
## [2,]  6.146571  5.821131 -5.884657 -6.232268
## 
## [[2]]
## [1] -3.811855  3.778289  9.346765  2.491479

Los pesos de la última capa son:

beta[3:4]
## [[1]]
##           [,1]
## [1,] -8.467028
## [2,]  9.779757
## [3,] -7.534183
## [4,]  8.753868
## 
## [[2]]
## [1] -1.558765

Ejercicio: interpreta la red en términos de qué unidades están encendidas (valor cercano a 1) o apagadas (valor cercano a 0). ¿Puedes ajustar este modelo con dos tres unidades intermedias? Haz varias pruebas: ¿qué dificultades encuentras?

11.5 Cálculo en redes: feed-forward

Ahora generalizamos lo que vimos arriba para definir la arquitectura básica de redes neuronales y cómo se hacen cálculos en las redes.

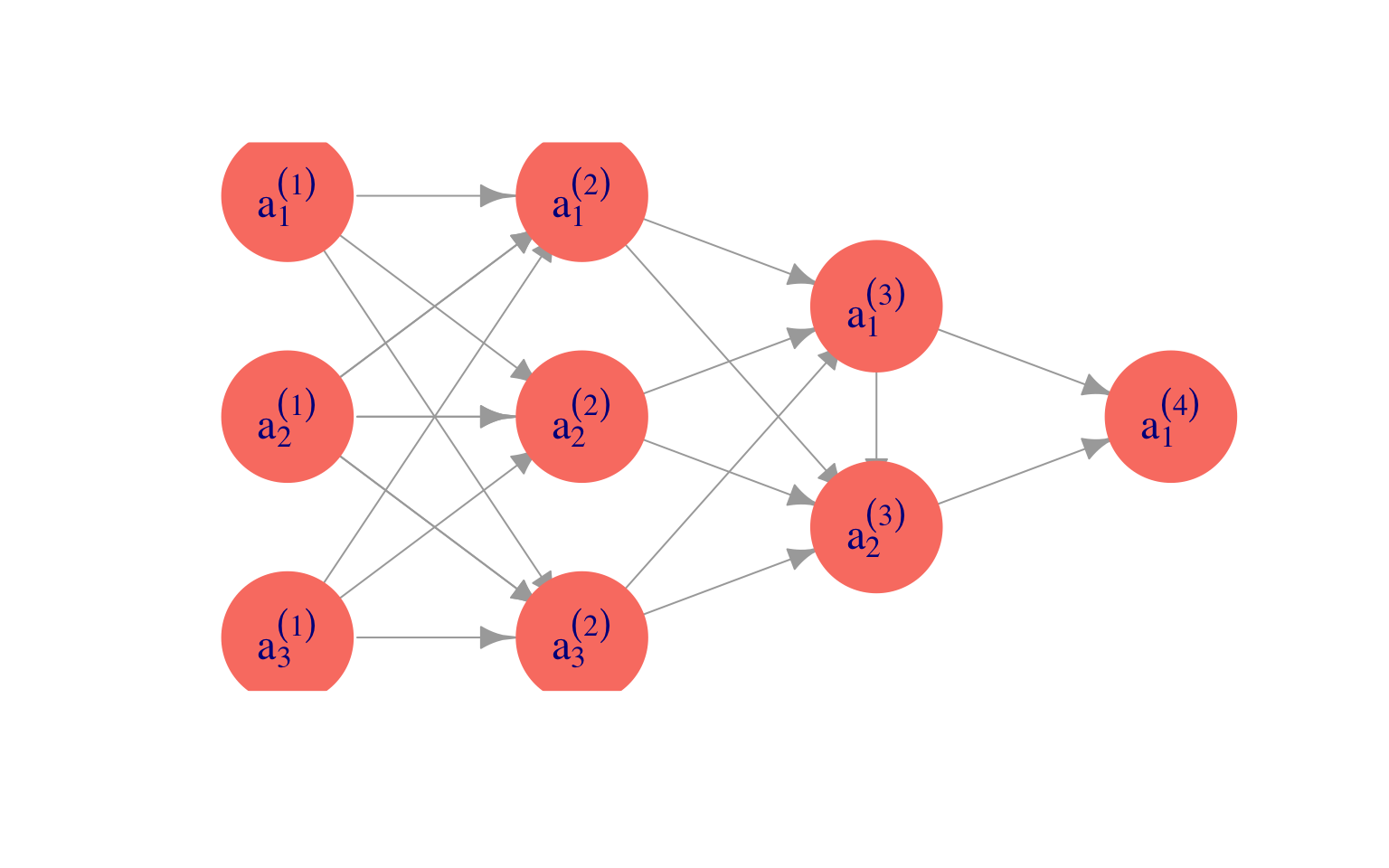
A las variables originales les llamamos capa de entrada de la red, y a la variable de salida capa de salida. Puede haber más de una capa intermedia. A estas les llamamos capas ocultas. Cuando todas las conexiones posibles de cada capa a la siguiente están presente, decimos que la red es completamente conexa.

Como vimos en el ejemplo de arriba, para hacer cálculos en la red empezamos con la primera capa, hacemos combinaciones lineales y aplicamos nuestra función no lineal \(h\). Una vez que calculamos la segunda capa, podemos calcular la siguiente de la misma forma: combinaciones lineales y aplicación de \(h\). Y así sucesivamente hasta que llegamos a la capa final.

Notación

Sea \(L\) el número total de capas. En primer lugar, para un cierto caso de entrada \(x = (x_1,x_2,\ldots, x_p)\), denotamos por:

  • \(a^{(l)}_j\) el valor que toma la unidad \(j\) de la capa \(l\), para \(j=0,1,\ldots, n_{l}\), donde \(n_l\) es el número de unidades de la capa \(l\).
  • Ponemos \(a^{(l)}_0=1\) para lidiar con los sesgos.
  • Ponemos \(a^{(1)}_j = x_j\), que son los valores de las entradas (primera capa)
  • La última capa solo tiene un elemento, que es \(f = a^{(L)}\). Si queremos predecir \(K\) salidas, tenemos que la última capa es de tamaño \(K\): \(f_1 = a^{(L)}_1, f_2 = a^{(L)}_2,\ldots, f_K = a^{(L)}_K\)

Adicionalmente, escribimos

  • \(\theta_{i,k}^{(l)}\) es el peso de la entrada \(a_{k}^{(l)}\) de la capa \(l\)
  • Los sesgos están dados por \[\theta_{i,0}^{(l)}\]

Ejemplo

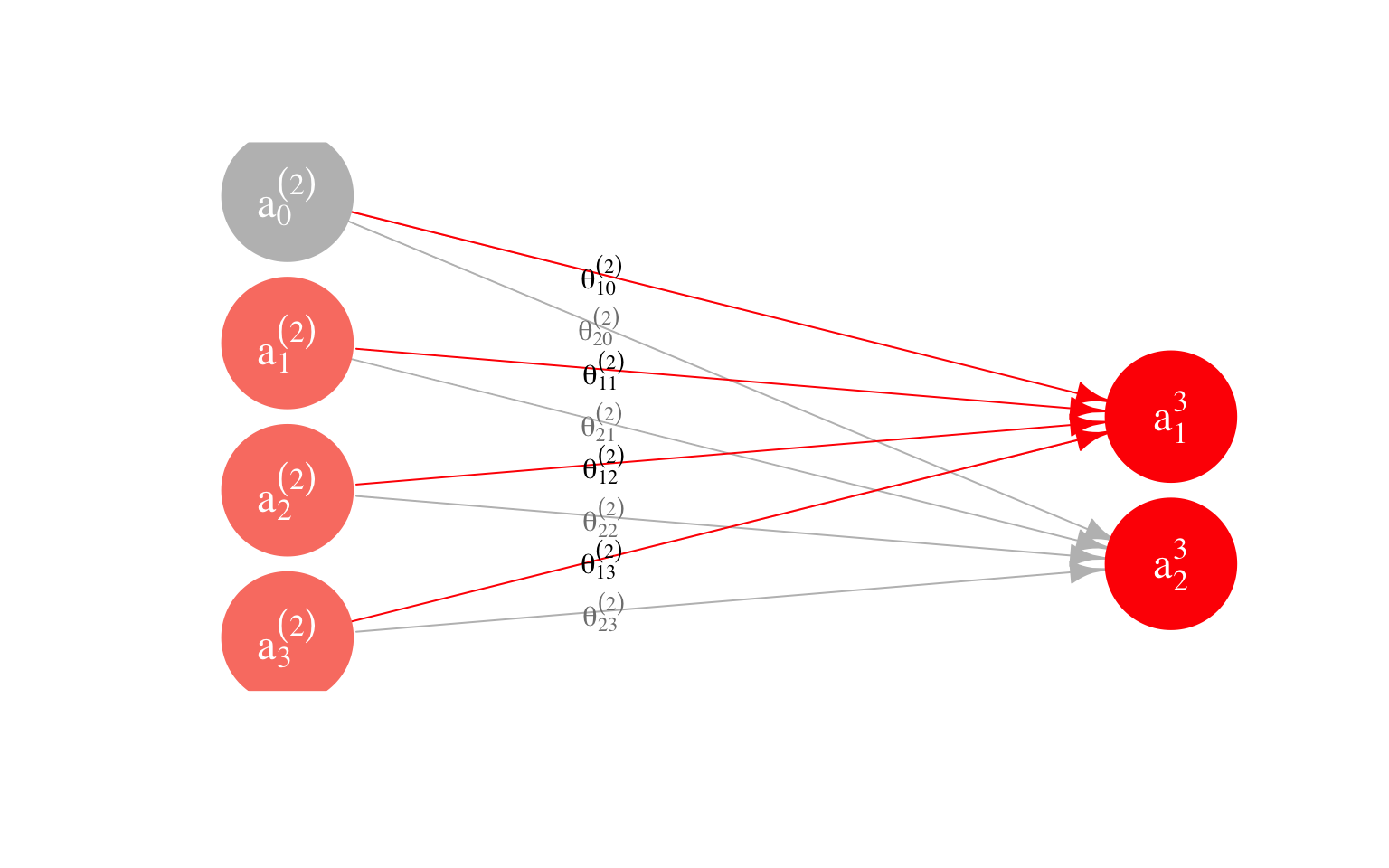
En nuestro ejemplo, tenemos que en la capa \(l=3\) hay dos unidades. Así que podemos calcular los valores \(a^{(3)}_1\) y \(a^{(3)}_2\). Están dados por

\[a_1^{(3)} = h(\theta_{1,0}^{(2)} + \theta_{1,1}^{(2)} a_1^{(2)}+ \theta_{1,2}^{(2)}a_2^{(2)}+ \theta_{1,3}^{(2)} a_3^{(2)})\] \[a_2^{(3)} = h(\theta_{2,0}^{(2)} + \theta_{2,1}^{(2)} a_1^{(2)}+ \theta_{2,2}^{(2)}a_2^{(2)}+ \theta_{2,3}^{(2)} a_3^{(2)})\]

Como se ilustra en la siguiente gráfica:

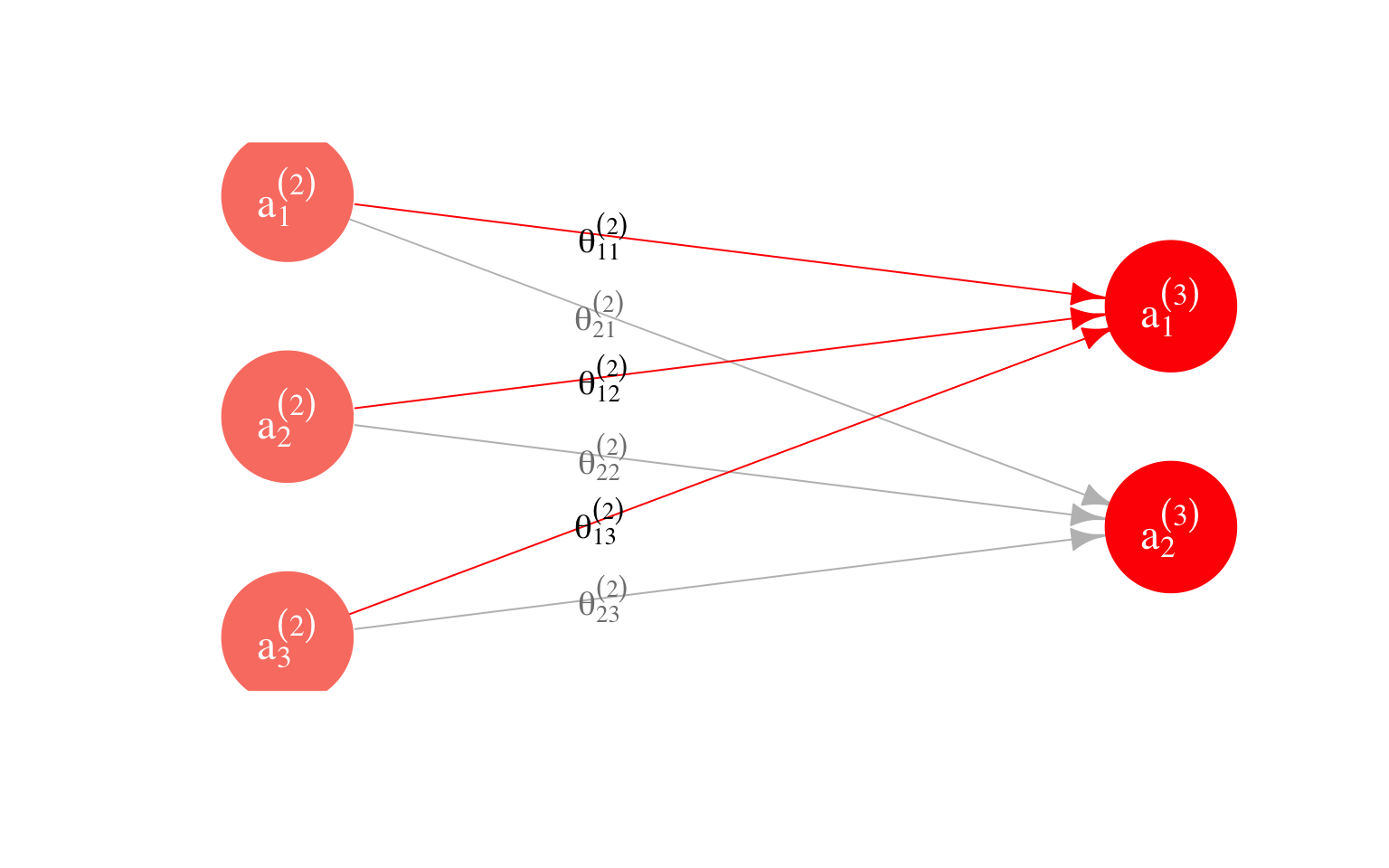
Para visualizar las ordenadas (que también se llaman sesgos en este contexto), ponemos \(a_{0}^{(2)}=1\).

Ejemplo

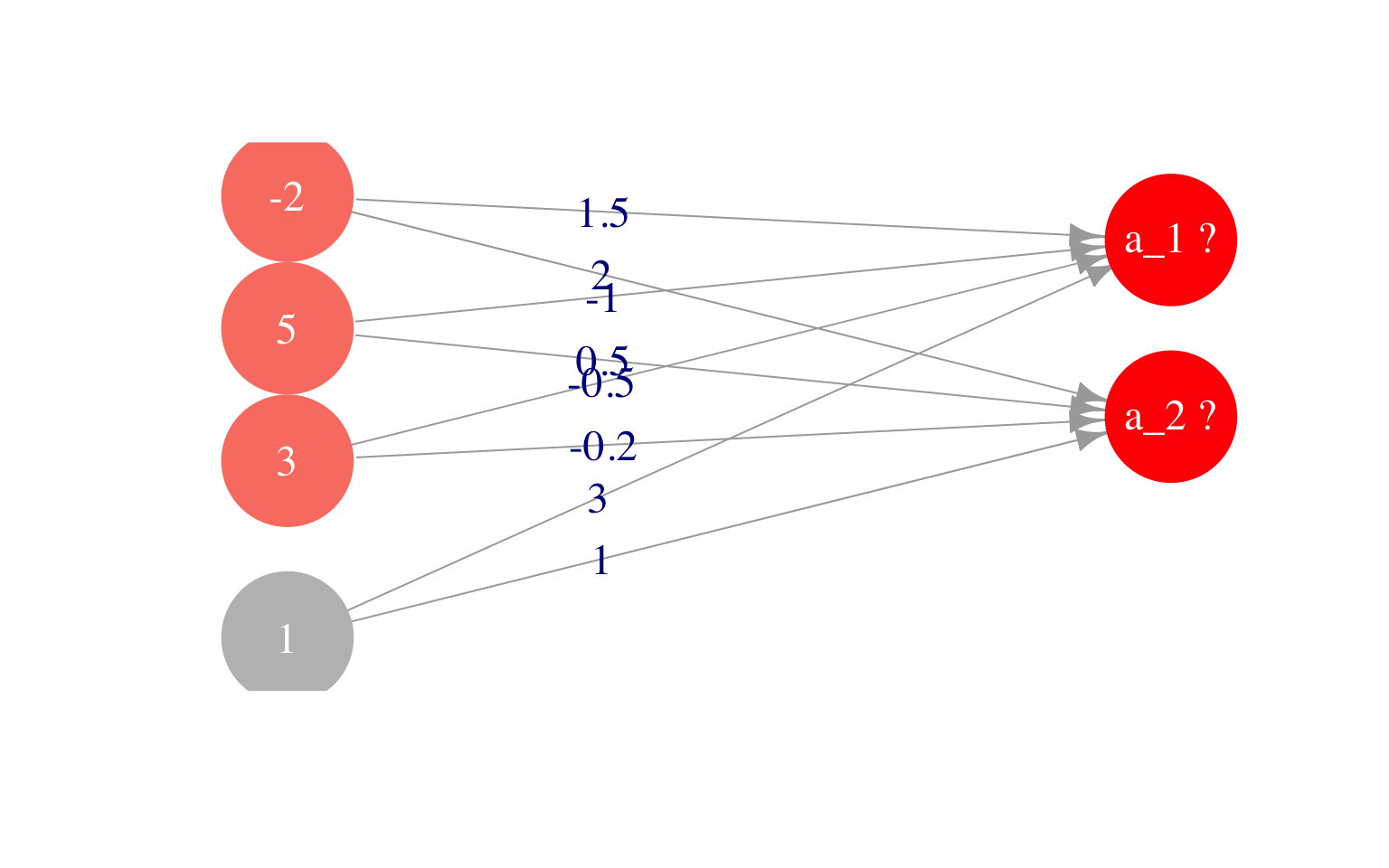
Consideremos propagar a la capa 3 a partir de la capa 2. Usaremos los siguientes pesos para capa 3 y valores de la capa 2 (en gris están los sesgos):

Que en nuestra notación escribimos como \[a^{(2)}_0 = 1, a^{(2)}_1 = -2, a^{(2)}_2 = 5, a^{(2)}=3\] y los pesos son, para la primera unidad: \[\theta^{(2)}_{1,0} = 3, \,\,\, \theta^{(2)}_{1,1} = 1.5,\,\,\,\theta^{(2)}_{1,2} = -1,\,\,\theta^{(2)}_{1,3} = -0.5 \] y para la segunda unidad \[\theta^{(2)}_{2,0} = 1, \,\,\, \theta^{(2)}_{2,1} = 2,\,\,\,\theta^{(2)}_{2,2} = 0.5,\,\, \theta^{(2)}_{2,3} = -0.2\] Y ahora queremos calcular los valores que toman las unidades de la capa 3, que son \(a^{(3)}_1\) y \(a^{(3)}_2\)$

Para hacer feed forward a la siguiente capa, hacemos entonces

\[a^{(3)}_1 = h(3 + a^{(2)}_1 - a^{(2)}_2 -0.5 a_3^{(2)}),\] \[a^{(3)}_2 = h(1 + 2a^{(2)}_1 + 0.5a^{(2)}_2 - 0.2 a_3^{(2)}),\]

Ponemos los pesos y valores de la capa 2 (incluyendo sesgo):

a_2 <- c(1, -2, 5, 3) # ponemos un 1 al principio para el sesgo
theta_2_1 = c(3, 1.5, -1.0, -0.5)
theta_2_2 = c(1, 2, 0.5, -0.2)

y calculamos

a_3 <- c(1, h(sum(theta_2_1*a_2)),h(sum(theta_2_2*a_2))) # ponemos un 1 al principio
a_3
## [1] 1.000000000 0.001501182 0.249739894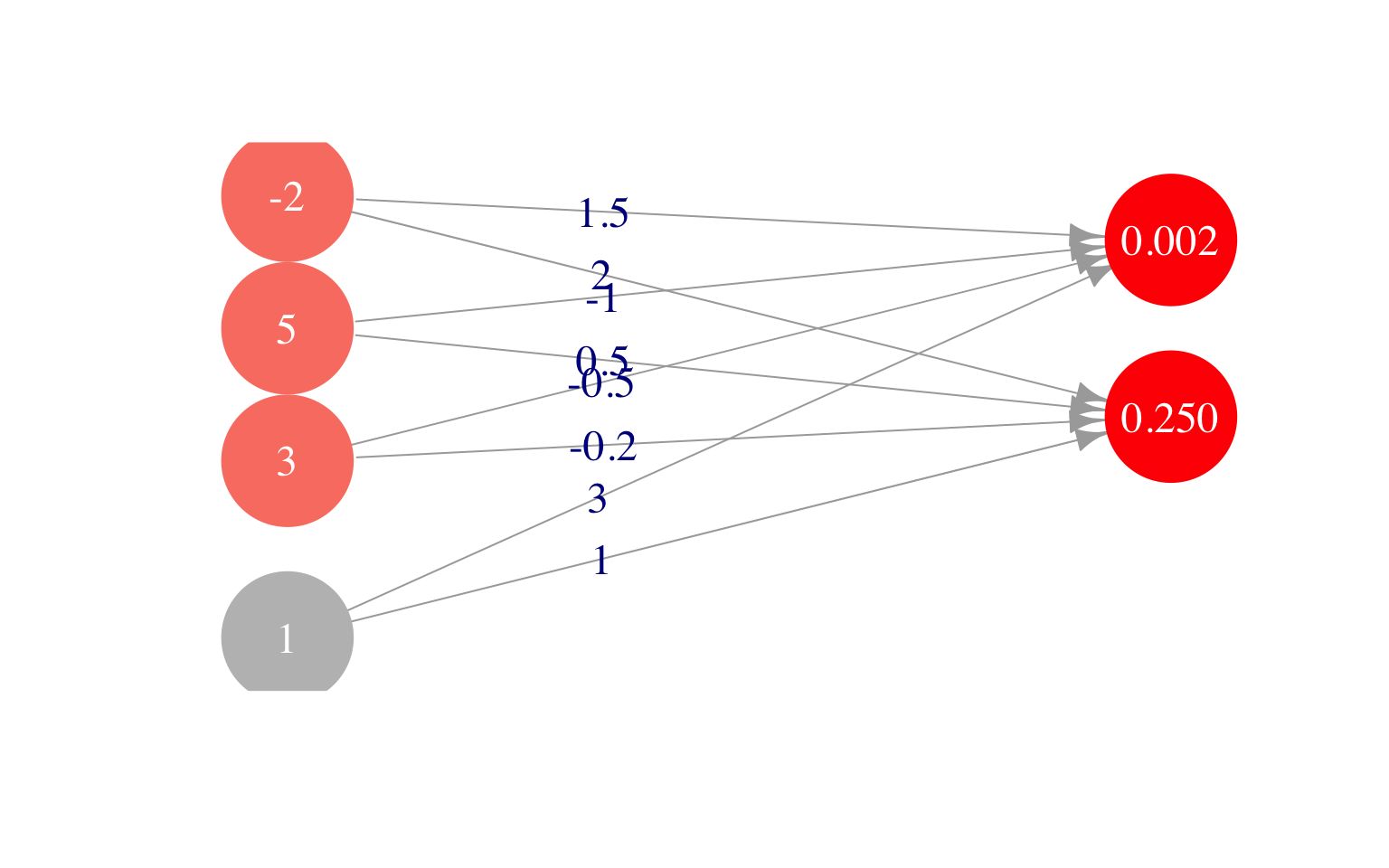

11.6 Algoritmo de Feed forward

Para calcular los valores de salida de una red a partir de pesos y datos de entrada, usamos el algoritmo feed-forward, calculando capa por capa.

Cálculo en redes: Feed-forward Para la primera capa, escribimos las variables de entrada: \[a^{(1)}_j = x_j, j=1\ldots,n_1\] Para la primera capa oculta, o la segunda capa \[a^{(2)}_j = h\left( \theta_{j,0}^{(1)}+ \sum_{k=1}^{n_1} \theta_{j,k}^{(1)} a^{(1)}_k \right), j=1\ldots,n_2\] para la \(l\)-ésima capa: \[a^{(l)}_j = h\left( \theta_{j,0}^{(l-1)}+ \sum_{k=1}^{n_{l-1}} \theta_{j,k}^{(l-1)} a^{(l-1)}_k \right), j=1\ldots,n_{l}\] y así sucesivamente. Para la capa final o capa de salida (para problema binario), suponiendo que tenemos \(L\) capas (\(L-2\) capas ocultas): \[f = \theta_{1,0}^{(L-1)}+ \sum_{k=1}^{n_{L-1}} \theta_{1,k}^{(L-1)} a^{(L-1)}_k .\]

Nótese que entonces:

Cada capa se caracteriza por el conjunto de parámetros \(\Theta^{(l)}\), que es una matriz de \(n_{l+1}\times n_{l}\). La red completa entonces se caracteriza por: - La estructura elegida (número de capas ocultas y número de nodos en cada capa oculta). - Las matrices de pesos en cada capa \(\Theta^{(1)},\Theta^{(2)},\ldots, \Theta^{(L-1)}\)

Adicionalmente, escribimos en forma vectorial: \[a^{(l)} = (a^{(l)}_0, a^{(l)}_1, a^{(l)}_2, \ldots, a^{(l)}_{n_l})^t\]

Para calcular la salidas, igual que hicimos, antes, propagaremos hacia adelante los valores de las variables de entrada usando los pesos. Agregando entradas adicionales en cada capa \(a_0^{(l)}\), \(l=1,2,\ldots, L-1\), donde \(a_0^{l}=1\), y agregando a \(\Theta^{(l)}\) una columna con las ordenadas al origen (o sesgos) podemos escribir:

Feed-forward(matricial) - Capa 1 (vector de entradas) \[ a^{(1)} = x\] - Capa 2 \[ a^{(2)} = h(\Theta^{(1)}a^{(1)})\] - Capa \(l\) (oculta) \[ a^{(l)} = h(\Theta^{(l-1)}a^{(l-1)})\] - Capa de salida:

En un problema de regresión, la capa de salida se calcula como en regresión lineal: \[a^{(L)}= f = \Theta^{(L-1)}a^{(L-1)}.\]

Nótese que feed-foward consiste principalmente de multiplicaciones de matrices con algunas aplicaciones de \(h\)

11.7 Algoritmo de Backpropagation: cálculo del gradiente

Para ajustar los pesos y sesgos de las redes (valores \(\theta\)), utilizaremos descenso en gradiente y otros algoritmos derivados del gradiente (descenso estocástico).

Para lograr esto, necesitamos calcular el gradiente de la función objetivo (que es la devianza o el error de entrenamiento). La expresión para el gradiente:

  • Se puede calcular analíticamente, resultando en una expresión recursiva para los coeficientes. Esto resulta en el algoritmo de backpropagation.
  • Se puede calcular de manera automática (usando diferenciación automática), que nos da un cálculo exacto sin necesidad de escribir todas las derivadas a mano. Plataformas como tensorflow toman este camino.

Abajo podemos ver el razonamiento (opcional) para hacer los cálculos analíticos:

En esta parte entonces veremos cómo calcular estos gradientes con el algoritmo de back-propagation, que es una aplicación de la regla de la cadena para derivar. Back-propagation resulta en una fórmula recursiva donde propagamos errores de la red como gradientes desde el final de red (capa de salida) hasta el principio, capa por capa.

Consideramos el problema de clasificación binaria

Recordamos la devianza (con regularización ridge) es

\[D = -\frac{1}{2n}\sum_{i=1}^n (y_i - f_i)^2 + \lambda \sum_{l=2}^{L} \sum_{k=1}^{n_{l-1}} \sum_{j=1}^{n_l}(\theta_{j,k}^{(l)})^2.\]

Queremos entonces calcular las derivadas de la devianza con respecto a cada parámetro \(\theta_{j,k}^{(l)}\). Esto nos proporciona el gradiente para nuestro algoritmo de descenso.

Consideramos aquí el problema de mínimos cuadrados y sin regularización. La parte de la parcial que corresponde al término de regularización es fácil de agregar al final.

Recordamos también nuestra notación para la función logística (o sigmoide):

\[h(z)=\frac{1}{1+e^{-z}}.\] Necesitaremos su derivada, que está dada por (cálculala): \[h'(z) = h(z)(1-h(z))\]

Cálculo para un caso de entrenamiento

Primero simplificamos el problema y consideramos calcular las parciales para un solo caso de entrenamiento \((x,y)\): \[ D= \frac{1}{2}(y-f)^2 . \]

Después sumaremos sobre toda la muestra de entrenamiento. Entonces queremos calcular \[\frac{\partial D}{\partial \theta_{j,k}^{(l)}}\]

Y escribiremos, con la notación de arriba, \[a^{(l+1)}_j = h(z^{(l+1)}_j)\] donde \[z^{(l+1)} = \Theta^{(l)} a^{(l)},\] que coordenada a coordenada se escribe como \[z^{(l+1)}_j = \sum_{k=0}^{n_{l}} \theta_{j,k}^{(l)} a^{(l)}_k\]

Paso 1: Derivar respecto a capa \(l+1\)

Como los valores de cada capa determinan los valores de salida y la devianza, podemos escribir (recordemos que \(a_0^{(l)}=1\) es constante): \[D=D(a_0^{(l+1)},a_1^{(l+1)},a_2^{(l+1)},\ldots, a_{n_{l+1}}^{(l+1)})=D(a_1^{(l+1)},a_2^{(l+1)},\ldots, a_{n_{l+1}}^{(l+1)})\]

Así que por la regla de la cadena para varias variables: \[\frac{\partial D}{\partial \theta_{j,k}^{(l)}} = \sum_{t=1}^{n_{l+1}} \frac{\partial D}{\partial a_t^{(l+1)}}\frac{\partial a_t^{(l+1)}} {\partial \theta_{j,k}^{(l)} }\]

Pero si vemos dónde aparece \(\theta_{j,k}^{(l)}\) en la gráfica de la red:

\[ \cdots a^{(l)}_k \xrightarrow{\theta_{j,k}^{(l)}} a^{(l+1)}_j \cdots \rightarrow D\] Entonces podemos concluir que \(\frac{\partial a_t^{(l+1)}}{\partial \theta_{j,k}^{(l)}} =0\) cuando \(t\neq j\) (pues no dependen de \(\theta_{j,k}^{(l)}\)),

y entonces, para toda \(j=1,2,\ldots, n_{l+1}, k=0,1,\ldots, n_{l}\) \[\begin{equation} \frac{\partial D}{\partial \theta_{j,k}^{(l)}} = \frac{\partial D}{\partial a_j^{(l+1)}}\frac{\partial a_j^{(l+1)}}{\partial \theta_{j,k}^{(l)} } . \tag{11.1} \end{equation}\]

Adicionalmente, como \[a_j^{(l+1)} = h(z_j^{(l+1)}) = h\left (\sum_{k=0}^{n_{l}} \theta_{j,k}^{(l)} a^{(l)}_k \right )\] y las \(a_k^{(l)}\) no dependen de \(\theta_{j,k}^{(l)}\), tenemos por la regla de la cadena que \[\begin{equation} \frac{\partial a_j^{(l+1)}}{\partial \theta_{j,k}^{(l)} } = h'(z_j^{(l+1)})a_k^{(l)}. \end{equation}\]

Esta última expresión podemos calcularla pues sólo requiere la derivada de \(h\) y los valores obtenidos en el paso de feed-forward.

Paso 2: Obtener fórmula recursiva

Así que sólo nos queda calcular las parciales (\(j = 1,\ldots, n_l\)) \[\frac{\partial D}{\partial a_j^{(l)}}\]

Para obtener una fórmula recursiva para esta cantidad (hacia atrás), aplicamos otra vez regla de la cadena, pero con respecto a la capa \(l\) (ojo: queremos obtener una fórmula recursiva!):

\[\frac{\partial D}{\partial a_j^{(l)}}= \sum_{s=1}^{n_{l+1}} \frac{\partial D}{\partial a_s^{(l+1)}}\frac{\partial a_s^{(l+1)}}{\partial a_j^{(l)}},\]

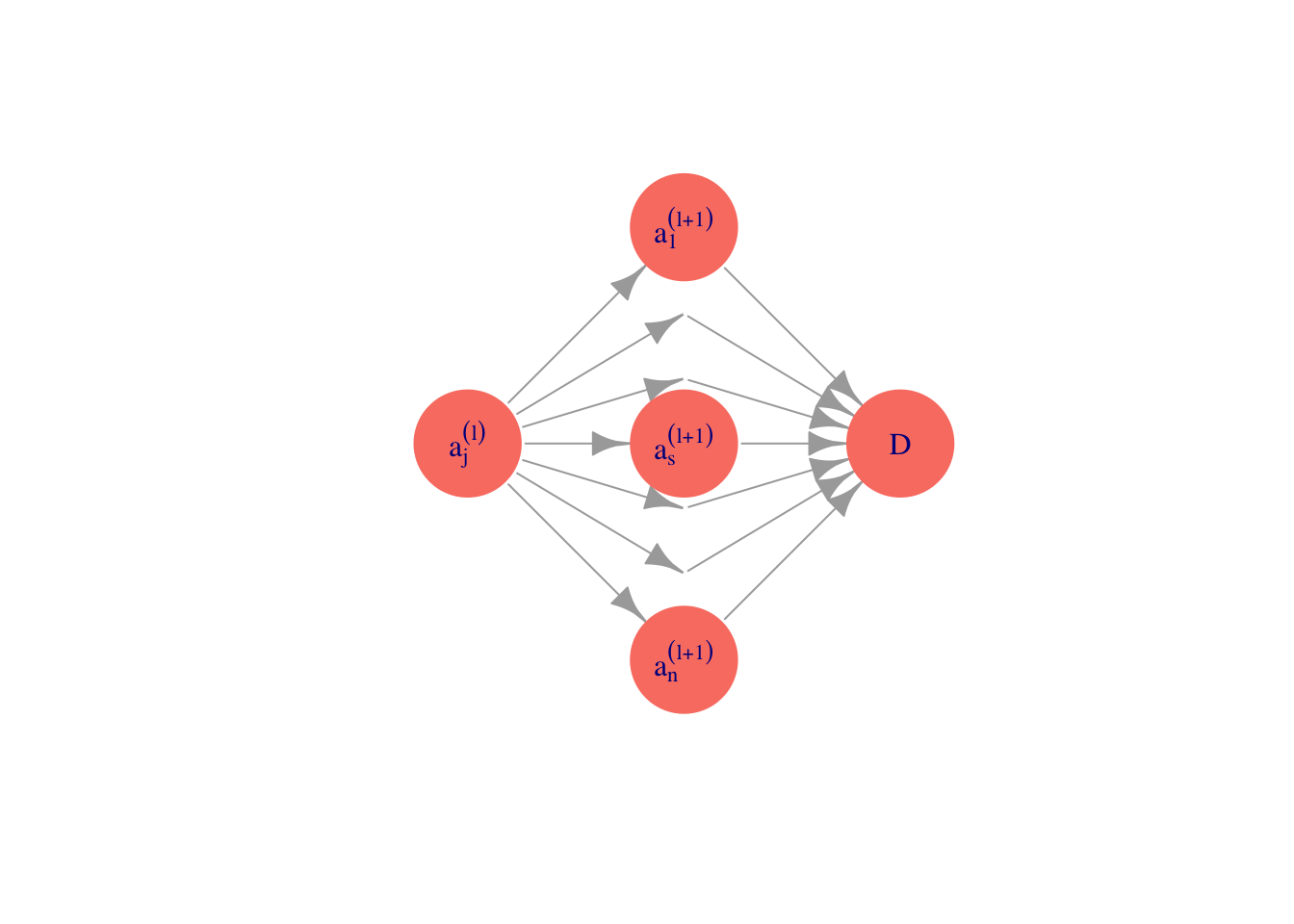
que se puede entender a partir de este diagrama:

Nótese que la suma empieza en \(s=1\), no en \(s=0\), pues \(a_0^{(l+1)}\) no depende de \(a_k^{(l)}\).

En este caso los elementos de la suma no se anulan necesariamente. Primero consideramos la derivada de:

\[\frac{\partial a_s^{(l+1)}}{\partial a_j^{(l)}}=h'(z_s^{(l+1)})\theta_{s,j}^{(l)},\]

de modo que

\[\frac{\partial D}{\partial a_j^{(l)}}= \sum_{s=1}^{n_l} \frac{\partial D}{\partial a_s^{(l+1)}} h'(z_s^{(l+1)})\theta_{s,j}^{(l)}.\]

Nótese que esto nos da una fórmula recursiva para las parciales que nos falta calcular (de \(D\) con respecto a \(a\)), pues las otras cantidades las conocemos por backpropagation.

Paso 3: Simplificación de la recursión

Definimos (para \(l < L-1\)):

\[\begin{equation} \delta_s^{ (l+1)}=\frac{\partial D}{\partial a_s^{(l+1)}} h'(z_s^{(l+1)}) \tag{11.2} \end{equation}\]

de manera que la ecuación recursiva es

\[\begin{equation} \frac{\partial D}{\partial a_j^{(l)}} = \sum_{s=1}^{n_{l+1}} \delta_s^{(l+1)}\theta_{s,j}^{(l)}. \tag{11.3} \end{equation}\]

Tenemos que si \(l=2,\ldots,L-1\), entonces podemos escribir (usando (11.3)) como fórmula recursiva:

\[\begin{equation} \delta_j^{(l)} = \left (\sum_{s=1}^{n_l} \delta_s^{(l+1)} \theta_{s,j}^{(l)}\right ) h'(z_j^{(l)}), \tag{11.4} \end{equation}\] para \(j=1,2,\ldots, n_{l}\).

Paso 4: Condiciones inciales

Para la última capa, tenemos que (demostrar!)

\[\delta_1^{(L)}=f - y.\]

Paso 5: Cálculo de parciales

Finalmente, usando (11.1) y (11.2) , obtenemos \[\frac{\partial D}{\partial \theta_{j,k}^{(l)}} = \delta_j^{(l+1)}a_k^{(l)},\]

y con esto ya podemos hacer backpropagation para calcular el gradiente sobre cada caso de entrenamiento, y solo resta acumular para obtener el gradiente sobre la muestra de entrenamiento.

Muchas veces es útil escribir una versión vectorizada (importante para implementar):

Paso 6: Versión matricial

Ahora podemos escribir estas ecuaciones en forma vectorial. En primer lugar, \[\delta^{(L)}=f-y.\] Y además se puede ver de la ecuación (11.4) que (\(\Theta_{*}^{(l+1)}\) denota la matriz de pesos sin la columna correspondiente al sesgo):

\[\begin{equation} \delta^{(l)}=\left( \Theta_{*}^{(l)} \right)^t\delta^{(l+1)} \circ h'(z^{(l)}) \tag{11.5} \end{equation}\]

donde \(\circ\) denota el producto componente a componente.

Ahora todo ya está calculado. Lo interesante es que las \(\delta^{(l)}\) se calculan de manera recursiva.

Algoritmo de backpropagation

Backpropagation Para problema de clasificación con regularización $ $. Para \(i=1,\ldots, N,\) tomamos el dato de entrenamiento \((x^{(i)}, y^{(i)})\) y hacemos:

  1. Ponemos \(a^{(1)}=x^{(i)}\) (vector de entradas, incluyendo 1).
  2. Calculamos \(a^{(2)},a^{(3)},\ldots, a^{(L)}\) usando feed forward para la entrada \(x^{(i)}.\)
  3. Calculamos \(\delta^{(L)}=a^{(L)}-y^{(i)}\), y luego \(\delta^{(L-1)},\ldots, \delta^{(2)}\) según la recursión (11.4).
  4. Acumulamos \(\Delta_{j,k}^{(l)}=\Delta_{j,k}^{(l)} + \delta_j^{(l+1)}a_k^{(l)}\).
  5. Finalmente, ponemos, si \(k\neq 0\), \[D_{j,k}^{(l)} = \frac{1}{N}\Delta_{j,k}^{(l)} + 2\lambda\theta_{j,k}^{(l)}\] y si \(k=0\), \[D_{j,k}^{(l)} = \frac{1}{N}\Delta_{j,k}^{(l)} .\] Entonces: \[D_{j,k}^{(l)} =\frac{\partial D}{\partial \theta_{j,k}^{(l)}}.\] Nótese que back-propagation consiste principalmente de mutliplicaciones de matrices con algunas aplicaciones de \(h\) y acumulaciones, igual que feed-forward.

11.8 Ajuste de parámetros (introducción)

Consideramos la versión con regularización ridge (también llamada L2) de la devianza de entrenamiento como nuestro función objetivo:

Ajuste de redes neuronales Para un problema de clasificación binaria con \(y_i=0\) o \(y_i=1\), ajustamos los pesos \(\Theta^{(1)},\Theta^{(2)},\ldots, \Theta^{(L)}\) de la red minimizando la devianza (penalizada) sobre la muestra de entrenamiento: \[D = -\frac{2}{n}\sum_{i=1}^n (y_i - f(x_i))^2 + \lambda \sum_{l=2}^{L} \sum_{k=1}^{n_{l-1}} \sum_{j=1}^{n_l}(\theta_{j,k}^{(l)})^2.\] Este problema en general no es convexo y puede tener múltiples mínimos.

Veremos el proceso de ajuste, selección de arquitectura, etc. más adelante. Por el momento hacemos unas observaciones acerca de este problema de minimización:

  • Hay varios algoritmos para minimizar esta devianza, algunos avanzados incluyendo información de segundo orden (como Newton), pero actualmente las técnicas más populares, para redes grandes, están derivadas de descenso en gradiente. Más específicamente, una variación, que es descenso estocástico.

  • Que el algoritmo depende principalmente de multiplicaciones de matrices y acumulaciones implica que puede escalarse de diversas maneras. Una es paralelizando sobre la muestra de entrenamiento (y calcular acumulados al final), pero también se pueden paralelizar las multiplicaciones de matrices (para lo cual los GPUs se prestan muy bien).

  • Para redes neuronales, el gradiente se calcula con un algoritmo que se llama back-propagation, que es una aplicación de la regla de la cadena para propagar errores desde la capa de salida a lo largo de todas las capas para ajustar los pesos y sesgos.

  • En estos problemas no buscamos el mínimo global, sino un mínimo local de buen desempeño. Puede haber múltiples mínimos, puntos silla, regiones relativamente planas, precipicios (curvatura alta). Nótese que la simetría implica que podemos obtener la misma red cambiando pesos entre neuronas y las conexiones correspondientes. Esto implica que necesariamente hay varios mínimos.

  • Todo esto dificulta el entrenamiento de redes neuronales grandes. Para redes grandes, ni siquiera esperamos a alcanzar un mínimo local, sino que nos a veces detenemos prematuramente cuando obtenemos el mejor desempeño posible.

  • Para este problema, no tiene sentido comenzar las iteraciones con todos los pesos igual a cero, pues las unidades de la red son simétricas: no hay nada que distinga una de otra si todos los pesos son iguales. Esto quiere decir que si iteramos, todas las neuronas van a aprender lo mismo.

  • Es importante no comenzar valores de los pesos grandes, pues las funciones logísticas pueden quedar en regiones planas donde la minimización es lenta, o podemos tener gradientes demasiado grandes y produzcan inestabilidad en el cálculo del gradiente.

  • El ajuste de la tasa de aprendizaje es más delicado que para problemas convexos. Generalmente lo tratamos con un hiperparámetro más que hay que afinar. Tasas demasiado grandes pueden llevarnos a mínimos locales relativamente malos.

  • Generalmente los pesos se inicializan al azar con variables independientes gaussianas o uniformes centradas en cero, y con varianza chica (por ejemplo \(U(-0.5,0.5)\)). Una recomendación es usar \(U(-1/\sqrt{m}, 1/\sqrt{m})\) donde \(m\) es el número de entradas. En general, hay que experimentar con este parámetro.

El proceso para ajustar una red es entonces:

  • Definir número de capas ocultas, número de neuronas por cada capa, y un valor del parámetro de regularización. Estandarizar las entradas.
  • Seleccionar parámetros al azar para \(\Theta^{(2)},\Theta^{(3)},\ldots, \Theta^{(L)}\). Se toman, por ejemplo, normales con media 0 y varianza chica.
  • Correr un algoritmo de minimización de la devianza mostrada arriba. Es necesario experimentar con los parámetros del algoritmo de minimización.
  • Verificar convergencia del algoritmo a un mínimo local (o el algoritmo no está mejorando).
  • Predecir usando el modelo ajustado.

Finalmente, podemos probar distintas arquitecturas y valores del parámetros de regularización, para afinar estos parámetros según validación cruzada o una muestra de validación.

11.9 Acerca de redes totalmente conexas

La arquitectura de redes que introdujimos apenas (totalmente conexas) generalmente tienen un desempeño relativemnte pobre comparado con otros métodos como regresión y métodos basados en árboles, aunque con algo de esfuerzo y experimentación pueden afinarse para producir resultados buenos. El éxito actual de las redes neuronales para varios problemas (imágenes, texto, audio) no es gracias a este tipo de arquitecturas.

Cuando las redes neuronales tienen ventajas grandes sobre otros métodos es cuando consideramos arquitecturas adecuadas para el problema de interés. Esto implica definir, con conocimiento de dominio, qué tipo de conexiones entre las capas debe haber, y que restricciones deben cumplir esas conexiones (y pesos). Ejemplo de estas arquitecturas son:

  • Redes convolucionales (para imágenes, sonido, texto).
  • Embeddings de palabras (para texto).
  • Otros tipos de estructuras que toman en cuenta la estructura secuencial de los datos (sonido, texto, series de tiempo).

Estos tipos de estructuras restringidas, cuando son apropiadas, reducen el tamaño de los modelos y de entrenamiento, y su varianza potencial sin aumentar demasiado el sesgo. En estos casos, junto con datos de tamaño y calidad apropiada, es posible obtener resultados que superan fácilmente a otros métodos, y explican el importante avance de las redes neuronales para los problemas mencionados arriba (imagenes, sonido, texto por ejemplo).

11.10 Descenso estocástico

El algoritmo básico más popular para ajustar redes grandes es descenso estocástico y varios derivados, que son modificaciones de nuestro algoritmo de descenso en gradiente. Antes de presentar las razones para usarlo, veremos cómo funciona para problemas con regresión lineal o logística.

En descenso estocástico por minilotes, el cálculo del gradiente se hace sobre una submuestra relativamente chica de la muestra de entrenamiento. En este contexto, a esta submuestra se le llama un minilote. En cada iteración, nos movemos en la dirección de descenso de ese minilote. La muestra de entrenamiento se divide entonces (al azar) en minilotes, y recorremos todos los minilotes haciendo una actualización de nuestros parámetros en cada minilote. Un recorrido sobre todos los minilotes se llama una época (las iteraciones se entienden sobre los minilotes).

Antes de escribir el algoritmo mostramos una implementación para regresión logística. Usamos las mismas funciones para calcular devianza y gradiente.

library(tidyverse)
# la devianza es la misma
devianza_calc <- function(x, y){
  dev_fun <- function(beta){
    y_ajustada <- as.matrix(cbind(1, x)) %*% beta 
    0.5 * mean((y - y_ajustada)^2)
  }
  dev_fun
}
# el cálculo del gradiente es el mismo, pero x_ent y y_ent serán diferentes
grad_calc <- function(x_ent, y_ent){
  salida_grad <- function(beta){
    y_ajustada <- as.matrix(cbind(1, x_ent)) %*% beta
    e <- y_ent - y_ajustada
    grad_out <- - as.numeric(t(cbind(1, x_ent)) %*% e) / nrow(x_ent)
    names(grad_out) <- c('Intercept', colnames(x_ent))
    grad_out
  }
  salida_grad
}

Y comparamos los dos algoritmos:

descenso <- function(n, z_0, eta, h_deriv){
  z <- matrix(0,n, length(z_0))
  z[1, ] <- z_0
  for(i in 1:(n-1)){
    z[i+1, ] <- z[i, ] - eta * h_deriv(z[i, ])
  }
  z
}
# esta implementación es solo para este ejemplo:
descenso_estocástico <- function(n_epocas, z_0, eta, minilotes){
  #minilotes es una lista
  m <- length(minilotes)
  z <- matrix(0, m*n_epocas, length(z_0))
  z[1, ] <- z_0
  for(i in 1:(m*n_epocas-1)){
    k <- i %% m + 1
    if(i %% m == 0){
      #comenzar nueva época y reordenar minilotes al azar
      minilotes <- minilotes[sample(1:m, m)]
    }
    h_deriv <- grad_calc(minilotes[[k]]$x, minilotes[[k]]$y)
    z[i+1, ] <- z[i, ] - eta * h_deriv(z[i, ])
  }
  z
}

Usaremos un ejemplo simulado de regresión para hacer algunos experimentos:

f_1 <- function(x){
  5 + x
}
set.seed(49121)
sim_datos <- function(n){
  x <- runif(n, 0, 100)
  f <- f_1(x)
  y <- f + rnorm(length(f), 0, 20)
  # con dos variables de ruido:
  dat <- tibble(x_1 = (x - mean(x))/sd(x), 
                x_2 = rnorm(length(x), 0, 1),
                x_3 = rnorm(length(x), 0, 1),
                f = f, y)
  dat |> select(x_1, x_2, x_3, y) 
}
dat_ent <- sim_datos(200)
dat_valid <- sim_datos(1000)

Los parámetros que minimizan la devianza son:

lm(y ~ x_1 + x_2+ x_3 , data = dat_ent) |> coef() |> 
  round(2)
## (Intercept)         x_1         x_2         x_3 
##       56.53       28.88        1.61       -3.36

Hacemos primero descenso en gradiente:

iteraciones_descenso <- descenso(200, z_0 = rep(0, 4), eta = 0.5,
         h_deriv = grad_calc(x_ent = as.matrix(dat_ent[,c('x_1','x_2','x_3'), drop =FALSE]), 
                             y_ent=dat_ent$y)) |>
  data.frame() |> rename(beta_1 = X2, beta_2 = X3)
ggplot(iteraciones_descenso, aes(x=beta_1, y=beta_2)) + geom_point()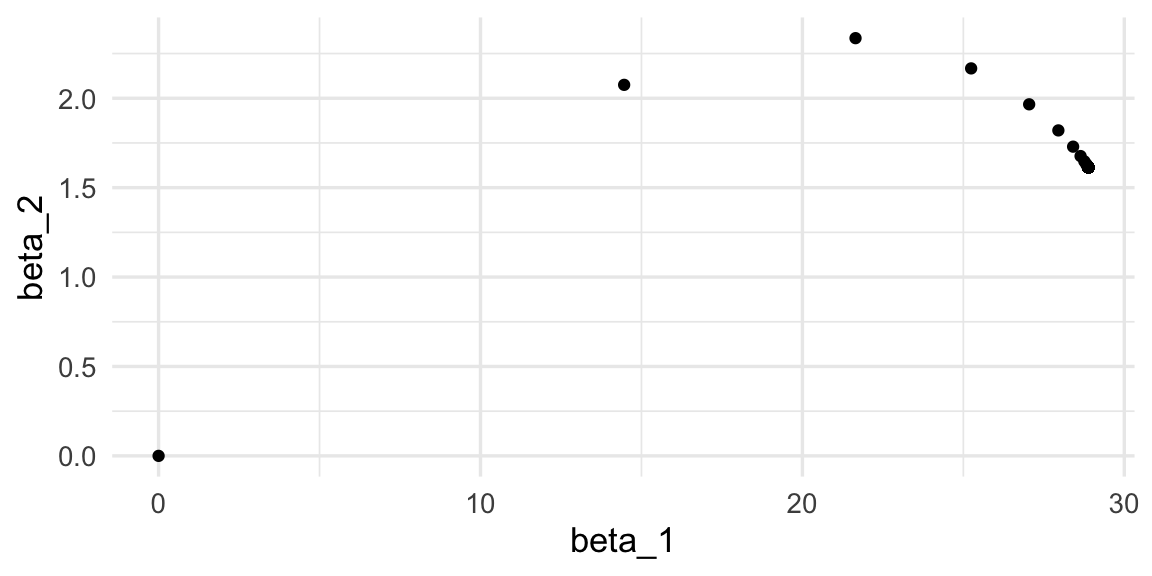

Y ahora hacemos descenso estocástico. Vamos a hacer minilotes de tamaño 10:

set.seed(2)
dat_ent$minilote <- rep(1:10, each = 20)
split_ml <- split(dat_ent |> sample_n(nrow(dat_ent)), dat_ent$minilote) 
minilotes <- lapply(split_ml, function(dat_ml){
  list(x = as.matrix(dat_ml[, c('x_1','x_2','x_3'), drop=FALSE]),
       y = dat_ml$y)
})
length(minilotes)
## [1] 10

Ahora iteramos. Nótese cómo descenso en gradiente tiene un patrón aleatorio de avance hacia el mínimo, y una vez que llega a una región oscila alrededor de este mínimo.

iter_estocastico <- descenso_estocástico(20, rep(0, 4), 0.03, minilotes) |>
  data.frame() |> rename(beta_0 = X1, beta_1 = X2, beta_2 = X3)
ggplot(iteraciones_descenso |> rename(beta_0 = X1), 
       aes(x=beta_1, y=beta_2)) + geom_path() +
  geom_point() +
  geom_path(data = iter_estocastico, colour ='red', alpha=0.2) +
  geom_point(data = iter_estocastico, colour ='red', alpha=0.2)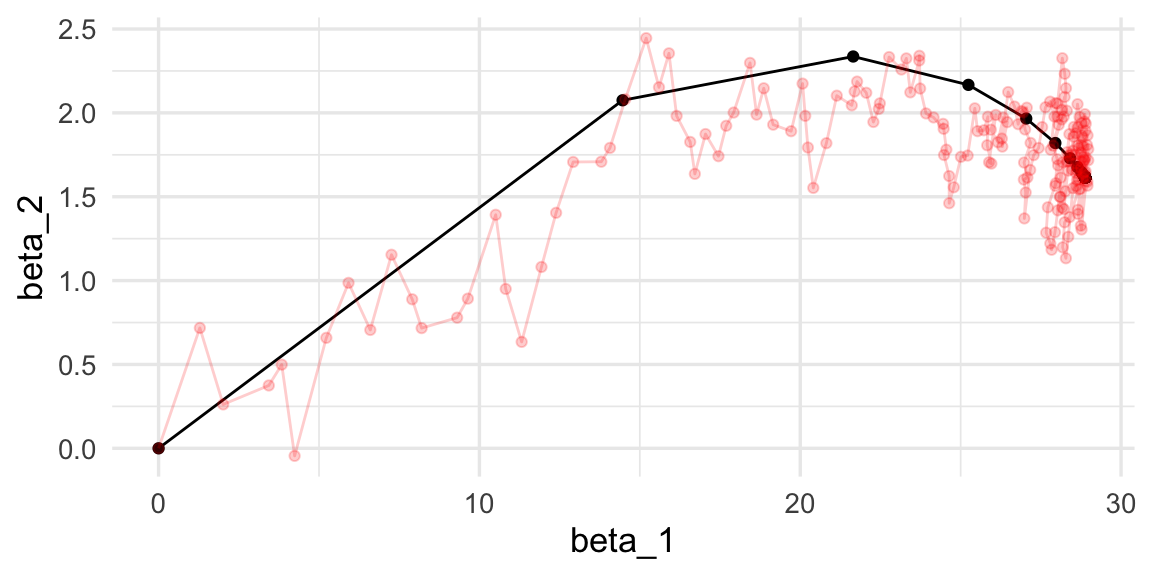

Podemos comparar contando el tiempo por época:

library(gganimate)
estocastico_tbl <- iter_estocastico
descenso_tbl <- iteraciones_descenso
estocastico_tbl$epoca <- 1:nrow(estocastico_tbl) / 10.0
descenso_tbl$epoca <- 1:nrow(descenso_tbl) / 1.0
descenso_tbl <- filter(descenso_tbl, epoca <= 20)
g_de <- ggplot(estocastico_tbl, aes(x = beta_1, y = beta_2)) + 
  geom_path(colour = "red") + geom_point(colour = "red") +
  geom_path(data = descenso_tbl) +
  geom_point(data = descenso_tbl, size = 3) +
  transition_reveal(epoca) 
animate(g_de, duration = 10)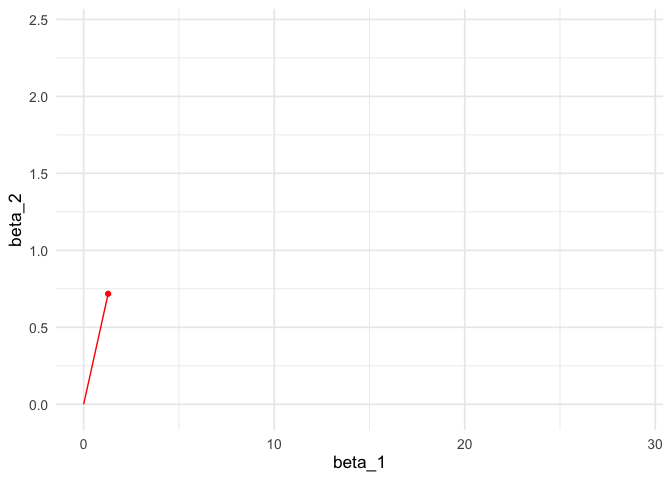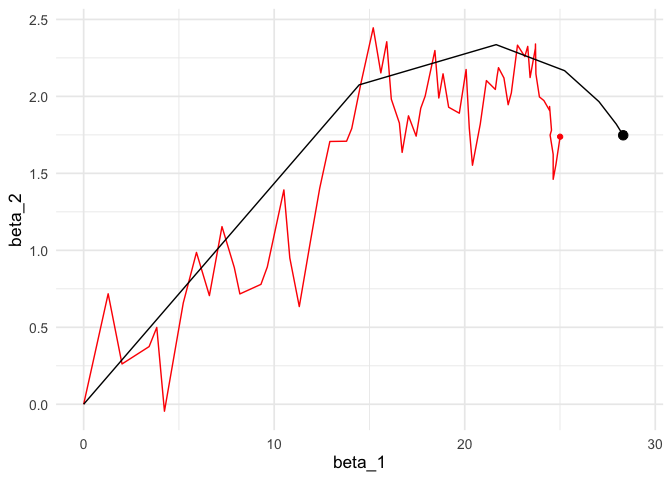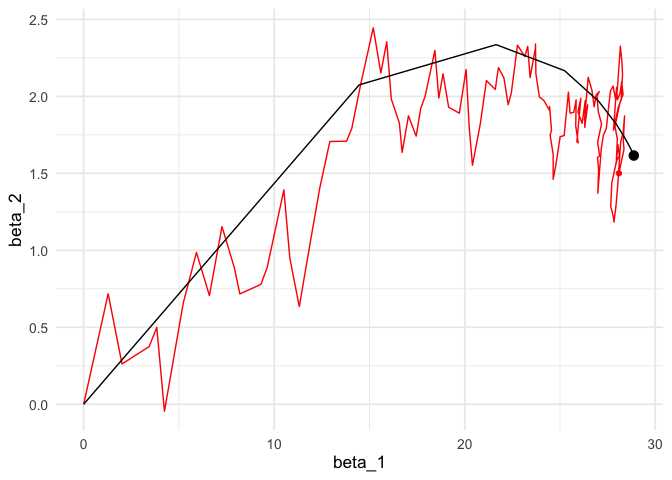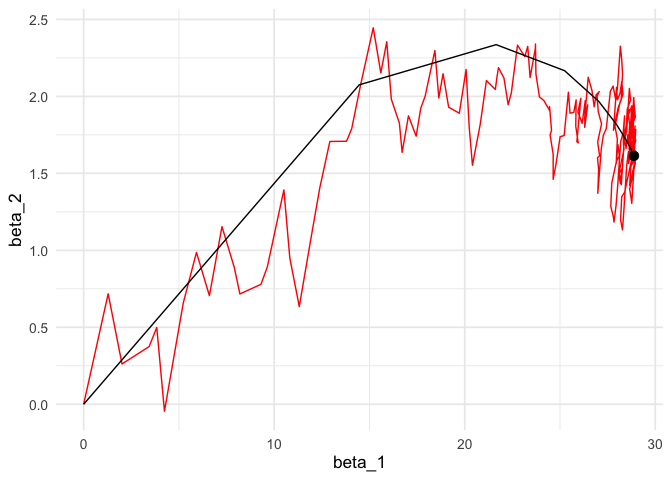

Podemos ver cómo se ve la devianza de entrenamiento:

dev_ent <- devianza_calc(x = as.matrix(dat_ent[,c('x_1','x_2','x_3'), drop =FALSE]), 
                             y=dat_ent$y)
dev_valid <- devianza_calc(x = as.matrix(dat_valid[,c('x_1','x_2','x_3'), drop =FALSE]),
                             y=dat_valid$y)
dat_dev <- tibble(iteracion = 1:nrow(iteraciones_descenso)) |>
  mutate(descenso = apply(iteraciones_descenso, 1, dev_ent),
        descenso_estocastico = apply(iter_estocastico, 1, dev_ent)) |>
  gather(algoritmo, dev_ent, -iteracion) |> mutate(tipo ='entrenamiento')
dat_dev_valid <- data_frame(iteracion = 1:nrow(iteraciones_descenso)) |>
  mutate(descenso = apply(iteraciones_descenso, 1, dev_valid),
         descenso_estocastico = apply(iter_estocastico, 1, dev_valid)) |>
  gather(algoritmo, dev_ent, -iteracion) |> mutate(tipo ='validación')
## Warning: `data_frame()` was deprecated in tibble 1.1.0.
## Please use `tibble()` instead.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_lifecycle_warnings()` to see where this warning was generated.
dat_dev <- bind_rows(dat_dev, dat_dev_valid)
ggplot(filter(dat_dev, tipo=='entrenamiento'), 
       aes(x=iteracion, y=dev_ent, colour=algoritmo)) + geom_line() +
  geom_point(size = 0.8) + facet_wrap(~tipo)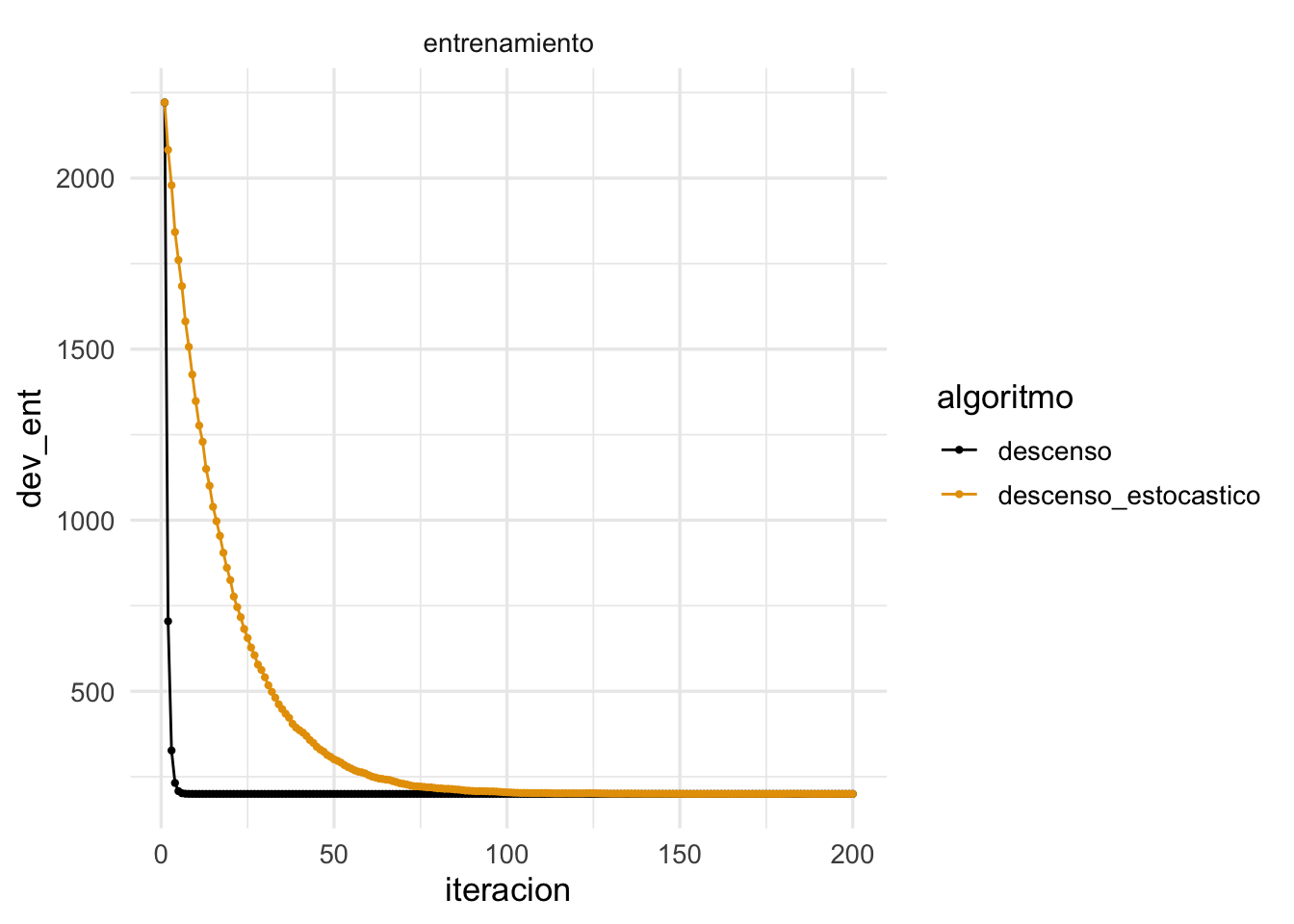

y vemos que descenso estocástico también converge a una buena solución.

11.11 Algoritmo de descenso estocástico

Descenso estocástico. Separamos al azar los datos de entrenamiento en \(n\) minilotes de tamaño \(m\). - Para épocas \(e =1,2,\ldots, n_e\) - Calcular el gradiente sobre el minilote y hacer actualización, sucesivamente para cada uno de los minilotes \(k=1,2,\ldots, n/m\): \[\beta_{i+1} = \beta_{i} - \eta\frac{1}{m}\sum_{j=1}^m \nabla D^{(k)}_j (\beta_i)\] donde \(D^{(k)}_j (\beta_i)\) es la devianza para el \(j\)-ésimo caso del minilote \(k\). - Repetir para la siguiente época (opcional: reordenar antes al azar los minibatches, para evitar ciclos).

11.12 ¿Por qué usar descenso estocástico por minilotes?

Las propiedades importantes de descenso estocástico son:

  1. Muchas veces no es necesario usar todos los datos para encontrar una buena dirección de descenso. Podemos ver la dirección de descenso en gradiente como un valor esperado sobre la muestra de entrenamiento (pues la pérdida es un promedio sobre el conjunto de entrenamiento). Una submuestra (minilote) puede ser suficiente para estimar ese valor esperado, con costo menor de cómputo. Adicionalmente, quizá no es tan buena idea intentar estimar el gradiente con la mejor precisión pues es solamente una dirección de descenso local (así que quizá no da la mejor decisión de a dónde moverse en cada punto). Es mejor hacer iteraciones más rápidas con direcciones estimadas.

  2. Desde este punto de vista, calcular el gradiente completo para descenso en gradiente es computacionalmente ineficiente. Si el conjunto de entrenamiento es masivo, descenso en gradiente no es factible.

  3. ¿Cuál es el mejor tamaño de minilote? Por un lado, minilotes más grandes nos dan mejores eficiencias en paralelización (multiplicación de matrices), especialmente en GPUs. Por otro lado, con minilotes más grandes puede ser que hagamos trabajo de más, por las razones expuestas en los incisos anteriores, y tengamos menos iteraciones en el mismo tiempo. El mejor punto está entre minilotes demasiado chicos (no aprovechamos paralelismo) o demasiado grande (hacemos demasiado trabajo por iteración).

4.La propiedad más importante de descenso estocástico en minilotes es que su convergencia no depende del tamaño del conjunto de entrenamiento, es decir, el tiempo de iteración para descenso estocástico no crece con el número de casos totales. Podemos tener obtener buenos ajustes incluso con tamaños muy grandes de conjuntos de entrenamiento (por ejemplo, antes de procesar todos los datos de entrenamiento). Descenso estocástico escala bien en este sentido: el factor limitante es el tamaño de minilote y el número de iteraciones.

  1. Es importante permutar al azar los datos antes de hacer los minibatches, pues órdenes naturales en los datos pueden afectar la convergencia. Se ha observado también que permutar los minibatches en cada iteración típicamente acelera la convergencia (si se pueden tener los datos en memoria).

11.13 Escogiendo la tasa de aprendizaje

Para escoger la tasa, monitoreamos las curvas de error de entrenamiento y de validación. Si la tasa es muy grande, habrá oscilaciones grandes y muchas veces incrementos grandes en la función objectivo (error de entrenamiento). Algunas oscilaciones suaves no tienen problema -es la naturaleza estocástica del algoritmo. Si la tasa es muy baja, el aprendizaje es lento y podemos quedarnos en un valor demasiado alto.

Conviene monitorear las primeras iteraciones y escoger una tasa más alta que la mejor que tengamos acutalmente, pero no tan alta que cause inestabilidad. Una gráfica como la siguiente es útil. En este ejemplo, incluso podríamos detenernos antes para evitar el sobreajuste de la última parte de las iteraciones:

ggplot(filter(dat_dev, algoritmo=='descenso_estocastico'), 
       aes(x=iteracion, y=dev_ent, colour=tipo)) + geom_line()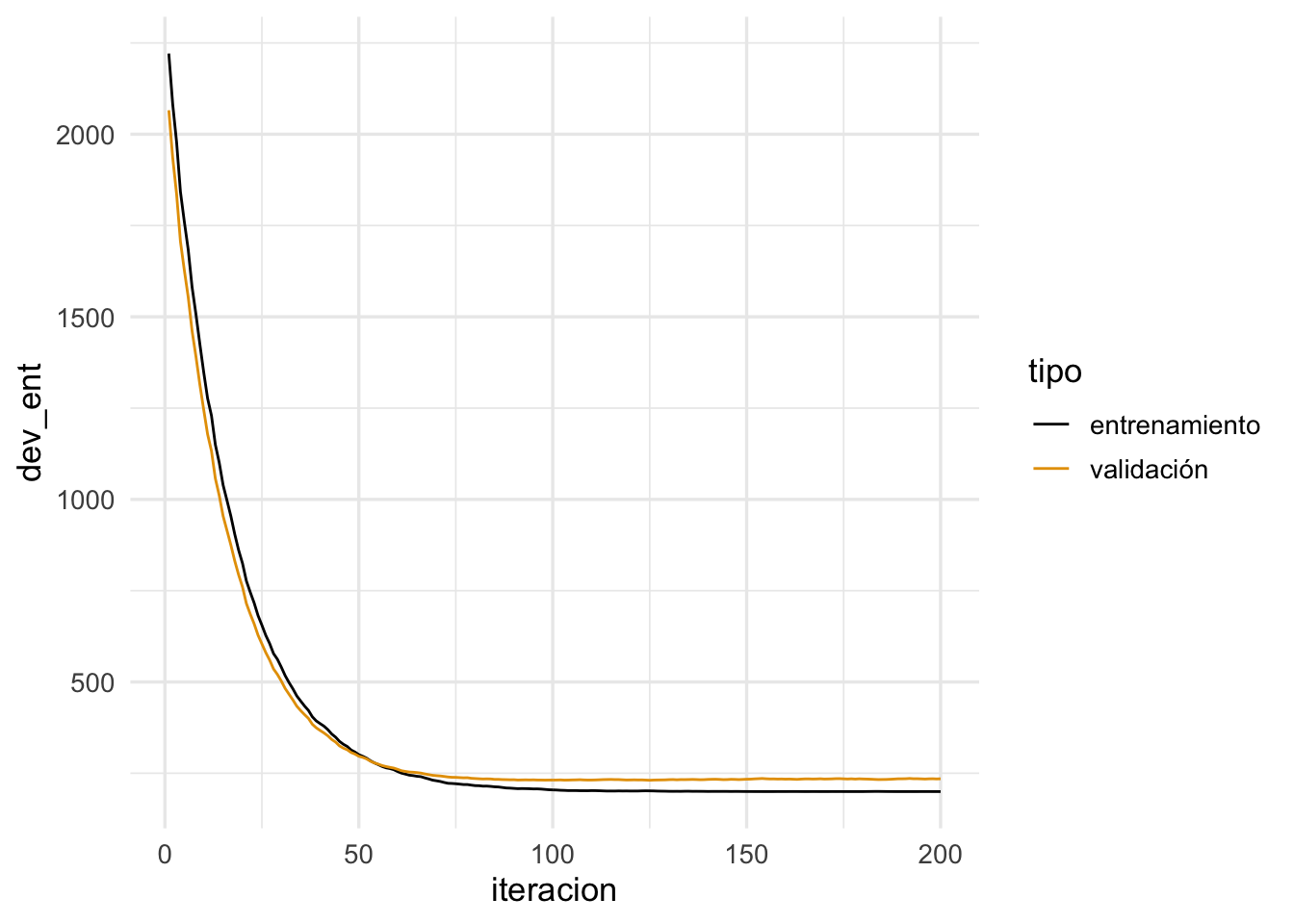

Por ejemplo: tasa demasiado alta:

iter_estocastico <- descenso_estocástico(20, rep(0,4), 0.99, minilotes) |>
  data.frame() |> rename(beta_0 = X1, beta_1 = X2)
dev_ent <- devianza_calc(x = as.matrix(dat_ent[,c('x_1','x_2','x_3'), drop =FALSE]), 
                             y=dat_ent$y)
dev_valid <- devianza_calc(x = as.matrix(dat_valid[,c('x_1','x_2','x_3'), drop =FALSE]), 
                             y=dat_valid$y)
dat_dev <- data_frame(iteracion = 1:nrow(iter_estocastico)) |>
   mutate(entrena = apply(iter_estocastico, 1, dev_ent), 
  validacion = apply(iter_estocastico, 1, dev_valid)) |>
  gather(tipo, devianza, entrena:validacion)
ggplot(dat_dev, 
       aes(x=iteracion, y=devianza, colour=tipo)) + geom_line()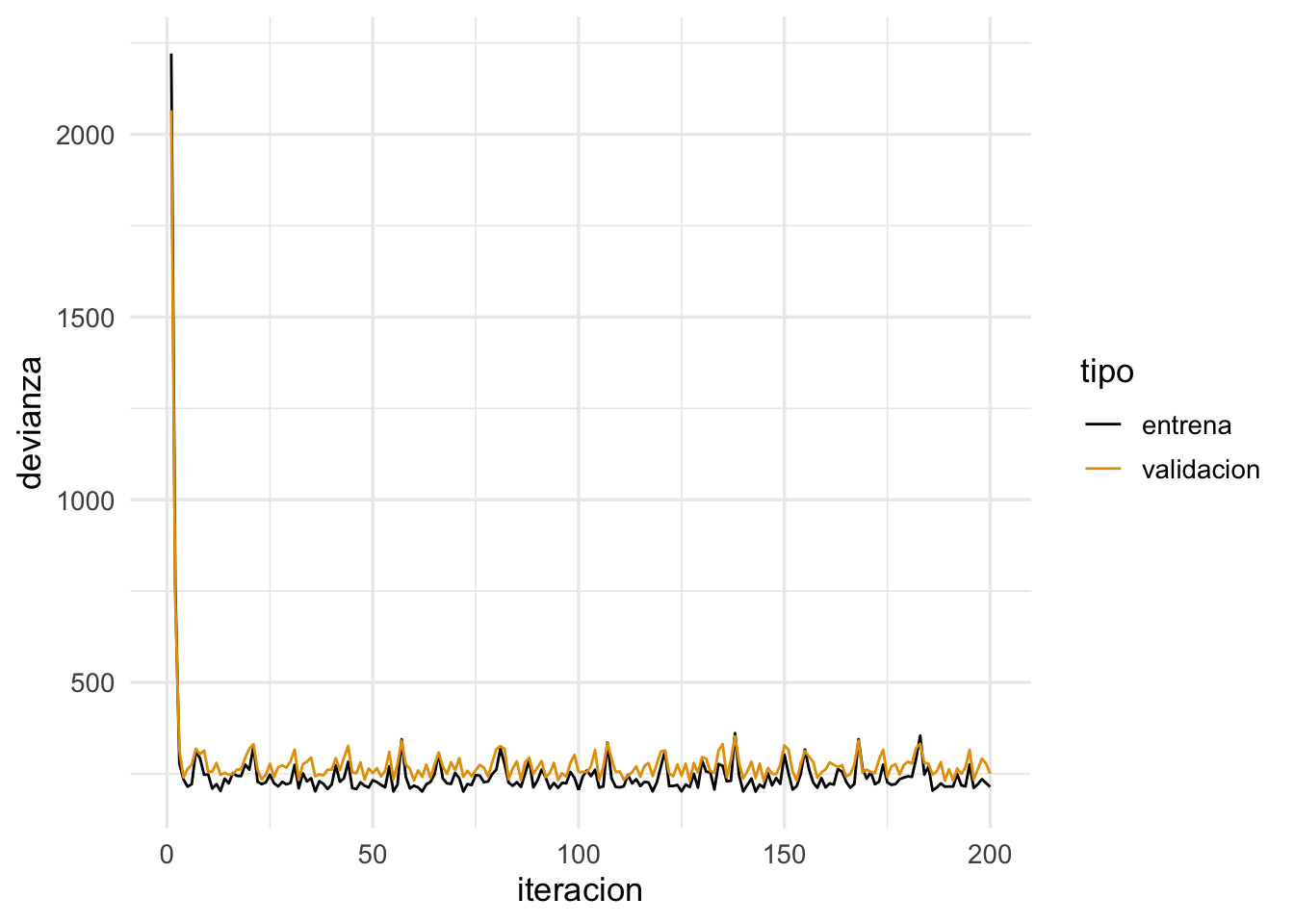

Tasa demasiado chica ( o hacer más iteraciones):

iter_estocastico <- descenso_estocástico(20, rep(0,4), 0.001, minilotes) |>
  data.frame() |> rename(beta_0 = X1, beta_1 = X2)
dev_ent <- devianza_calc(x = as.matrix(dat_ent[,c('x_1','x_2','x_3'), drop =FALSE]), 
                             y=dat_ent$y)
dev_valid <- devianza_calc(x = as.matrix(dat_valid[,c('x_1','x_2','x_3'), drop =FALSE]), 
                             y=dat_valid$y)
dat_dev <- data_frame(iteracion = 1:nrow(iter_estocastico)) |>
   mutate(entrena = apply(iter_estocastico, 1, dev_ent), 
  validacion = apply(iter_estocastico, 1, dev_valid)) |>
  gather(tipo, devianza, entrena:validacion)
ggplot(dat_dev, 
       aes(x=iteracion, y=devianza, colour=tipo)) + geom_line()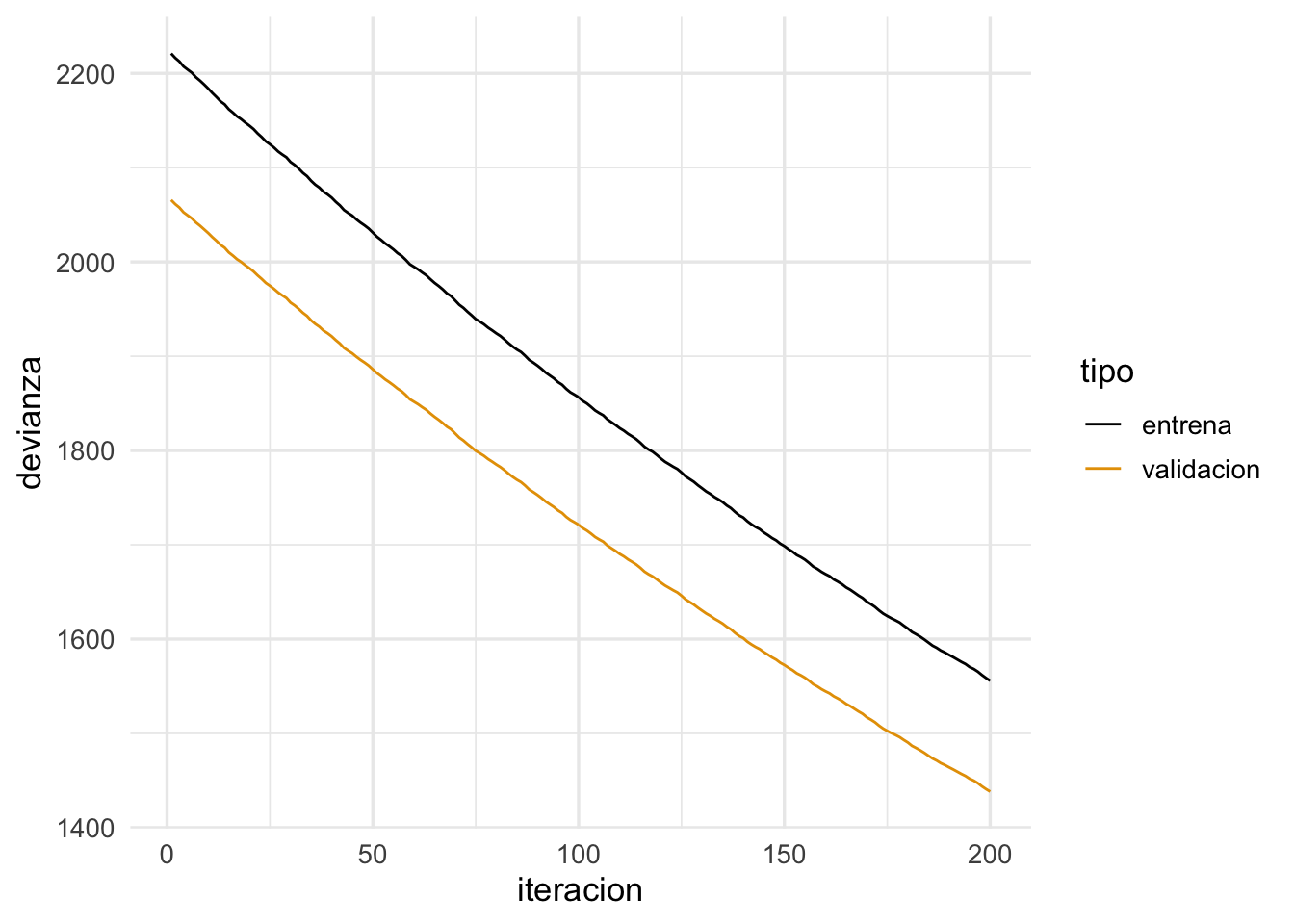
  • Para redes neuronales, es importante explorar distintas tasas de aprendizaje, aún cuando no parezca haber oscilaciones grandes o convergencia muy lenta. En algunos casos, si la tasa es demasiado grande, puede ser que el algoritmo llegue a lugares con gradientes cercanos a cero (por ejemplo, por activaciones demasiado grandes) y tenga dificultad para moverse.

11.14 Mejoras al algoritmo de descenso estocástico.

Decaimiento de tasa de aprendizaje

Hay muchos algoritmos derivados de descenso estocástico. La primera mejora consiste en reducir gradualmente la tasa de aprendizaje para aprender rápido al principio, pero filtrar el ruido de la estimación de minilotes más adelante en las iteraciones y permitir que el algoritmo se asiente en un mínimo.

descenso_estocástico <- function(n_epocas, z_0, eta, minilotes, decaimiento = 0.0){
  #minilotes es una lista
  m <- length(minilotes)
  z <- matrix(0, m*n_epocas, length(z_0))
  z[1, ] <- z_0
  for(i in 1:(m*n_epocas-1)){
    k <- i %% m + 1
    if(i %% m == 0){
      #comenzar nueva época y reordenar minilotes al azar
      minilotes <- minilotes[sample(1:m, m)]
    }
    h_deriv <- grad_calc(minilotes[[k]]$x, minilotes[[k]]$y)
    z[i+1, ] <- z[i, ] - eta * h_deriv(z[i, ])
    eta <- eta*(1/(1+decaimiento*i))
  }
  z
}

Y ahora vemos qué pasa con decaimiento:

iter_estocastico <- descenso_estocástico(50, c(0,0, 0, 0), 0.05, 
                                         minilotes, decaimiento = 1e-5) |>
  data.frame() |> rename(beta_0 = X1, beta_1 = X2, beta_2 = X3, beta_3 = X4)
dev_ent <- devianza_calc(x = as.matrix(dat_ent[,c('x_1','x_2','x_3'), drop =FALSE]), 
                             y=dat_ent$y)
dev_valid <- devianza_calc(x = as.matrix(dat_valid[,c('x_1','x_2','x_3'), drop =FALSE]), 
                             y=dat_valid$y)
dat_dev <- data_frame(iteracion = 1:nrow(iter_estocastico)) |>
   mutate(entrena = apply(iter_estocastico, 1, dev_ent), 
  validacion = apply(iter_estocastico, 1, dev_valid)) |>
  gather(tipo, devianza, entrena:validacion)
ggplot(filter(dat_dev, iteracion>1), 
       aes(x=iteracion, y=devianza, colour=tipo)) + geom_line()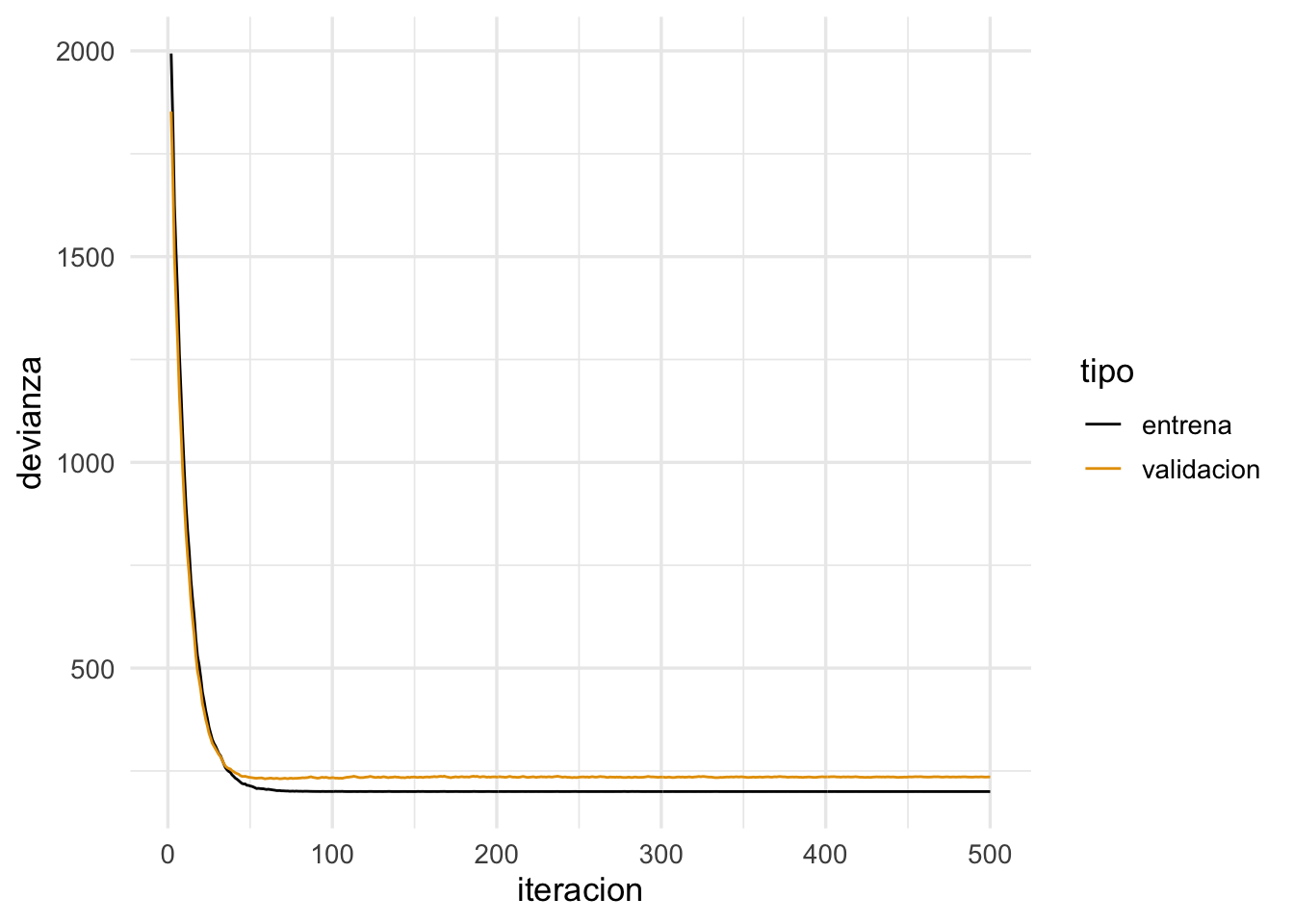

Para los primeros dos parámetros, las iteraciones se ven:

ggplot(iteraciones_descenso, aes(x=beta_1, y=beta_2)) + geom_path() +
  geom_point() +
  geom_path(data = iter_estocastico, colour ='red', alpha=0.2) +
  geom_point(data = iter_estocastico, colour ='red', alpha=0.2)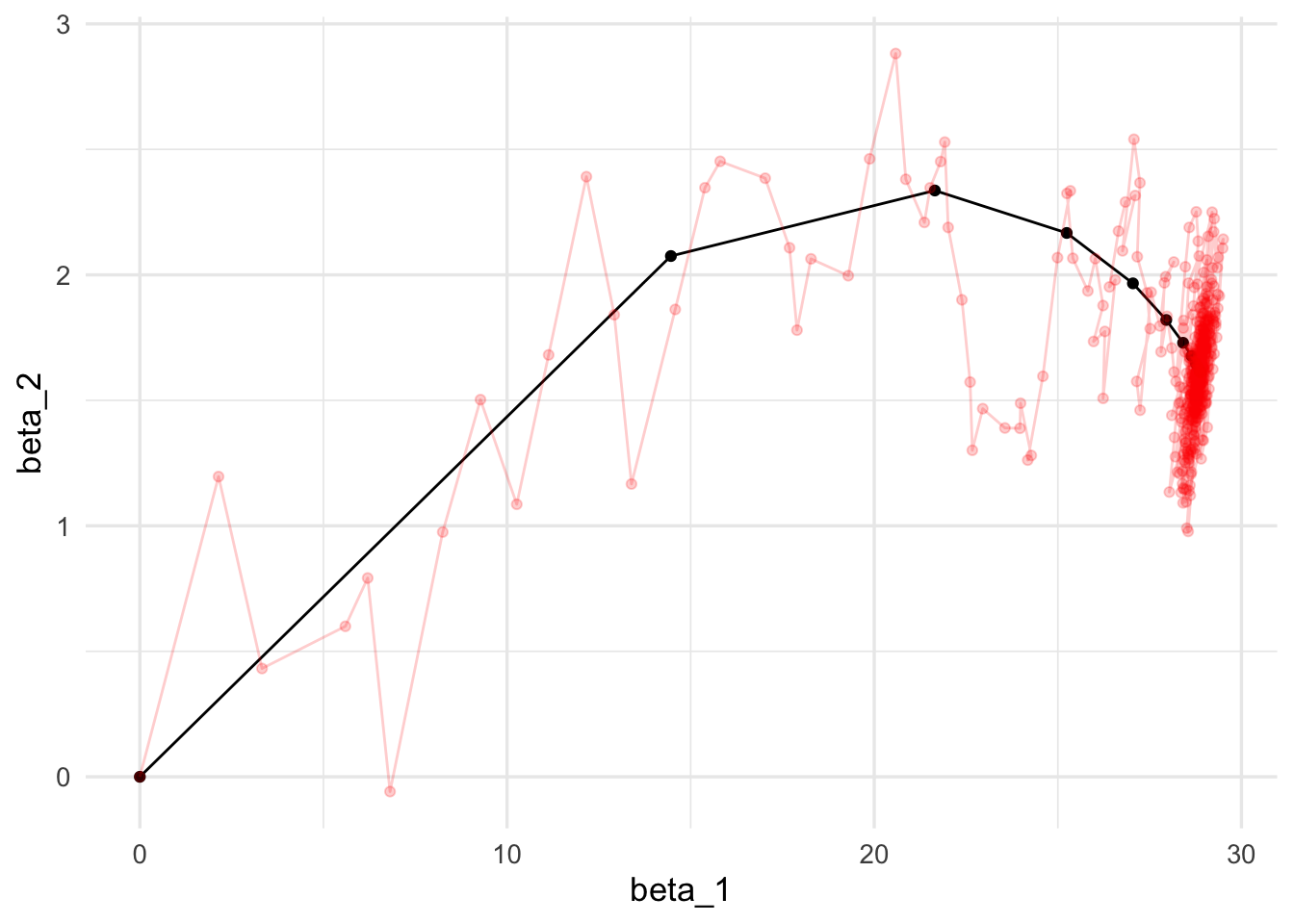
La tasa de aprendizaje es uno de los parámetros en redes neuronales más importantes de afinar. Generalmente se empieza con una tasa de aprendizaje con un valor bajo (0.01, o 0.1), pero es necesario experimentar. - Un valor muy alto puede provocar oscilaciones muy fuertes en la pérdida - Un valor alto también puede provocar que el algoritmo se detenga en lugar con función pérdida alta (sobreajusta rápidamente). - Un valor demasiado bajo produce convergencia lenta.

Momento

También es posible utilizar una idea adicional que acelera la convergencia. La idea es que muchas veces la aleatoriedad del algoritmo puede producir iteraciones en direcciones que no son tan buenas (pues la estimación del gradiente es mala). Esto es parte del algoritmo. Sin embargo, si en varias iteraciones hemos observado movimientos en direcciones consistentes, quizá deberíamos movernos en esas direcciones consistentes, y reducir el peso de la dirección del minilote (que nos puede llevar en una dirección mala). El resultado es un suavizamiento de las curvas de aprendizaje.

Esto es similar al movimiento de una canica en una superficie: la dirección de su movimiento está dada en parte por la dirección de descenso (el gradiente) y en parte la velocidad actual de la canica. La canica se mueve en un promedio de estas dos direcciones

Descenso estocástico con momento Separamos al azar los datos de entrenamiento en \(n\) minilotes de tamaño \(m\). - Para épocas \(e =1,2,\ldots, n_e\) - Calcular el gradiente sobre el minilote y hacer actualización, sucesivamente para cada uno de los minilotes \(k=1,2,\ldots, n/m\): \[\beta_{i+1} = \beta_{i} + v,\] \[v= \alpha v - \eta\frac{1}{m}\sum_{j=1}^m \nabla D^{(k)}_j\] donde \(D^{(k)}_j (\beta_i)\) es la devianza para el \(j\)-ésimo caso del minilote \(k\). A \(v\) se llama la velocidad - Repetir para la siguiente época 
descenso_estocástico <- function(n_epocas, z_0, eta, minilotes, 
                                 momento = 0.0, decaimiento = 0.0){
  #minilotes es una lista
  m <- length(minilotes)
  z <- matrix(0, m*n_epocas, length(z_0))
  z[1, ] <- z_0
  v <- 0
  for(i in 1:(m*n_epocas-1)){
    k <- i %% m + 1
    if(i %% m == 0){
      #comenzar nueva época y reordenar minilotes al azar
      minilotes <- minilotes[sample(1:m, m)]
      v <- 0
    }
    h_deriv <- grad_calc(minilotes[[k]]$x, minilotes[[k]]$y)
    z[i+1, ] <- z[i, ] + v
    v <- momento*v - eta * h_deriv(z[i, ])
    eta <- eta*(1/(1+decaimiento*i))
  }
  z
}

Y ahora vemos que usando momento el algoritmo es más parecido a descenso en gradiente usual (pues tenemos cierta memoria de direcciones anteriores de descenso):

set.seed(231)
iter_estocastico <- descenso_estocástico(10, c(0,0, 0, 0), 0.02, minilotes, 
                                         momento = 0.9, decaimiento = 0.0001) |>
  data.frame() |> rename(beta_0 = X1, beta_1 = X2, beta_2=X3, beta_3=X4)
dev_ent <- devianza_calc(x = as.matrix(dat_ent[,c('x_1','x_2','x_3'), drop =FALSE]), 
                             y=dat_ent$y)
dev_valid <- devianza_calc(x = as.matrix(dat_valid[,c('x_1','x_2','x_3'), drop =FALSE]), 
                             y=dat_valid$y)
dat_dev <- data_frame(iteracion = 1:nrow(iter_estocastico)) |>
   mutate(entrena = apply(iter_estocastico, 1, dev_ent), 
  validacion = apply(iter_estocastico, 1, dev_valid)) |>
  gather(tipo, devianza, entrena:validacion)
ggplot(filter(dat_dev, iteracion > 1), 
       aes(x=iteracion, y=devianza, colour=tipo)) + geom_line() + geom_point()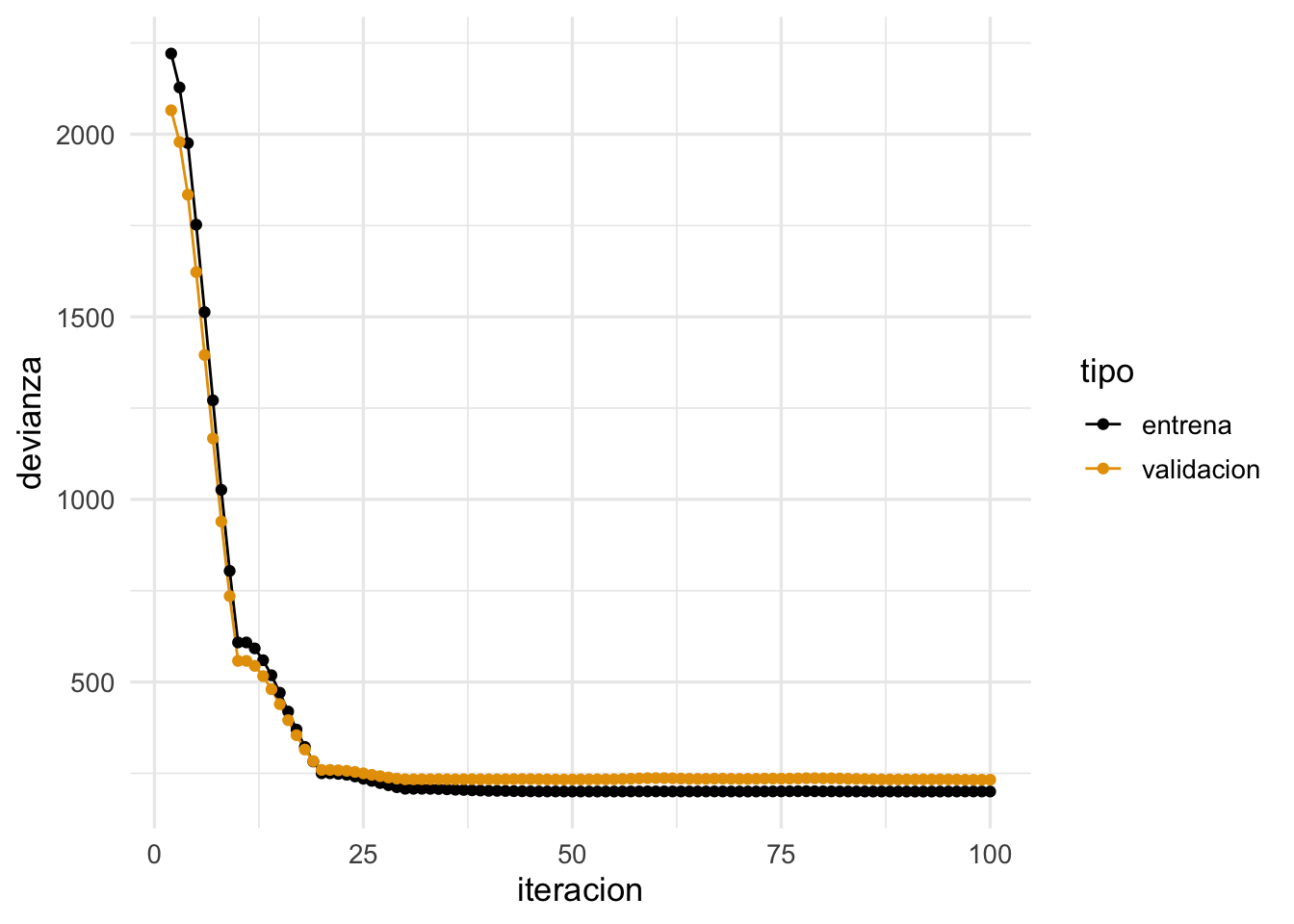
ggplot(iteraciones_descenso, aes(x=beta_1, y=beta_2)) + geom_path() +
  geom_point() +
  geom_path(data = iter_estocastico, colour ='red', alpha=0.5) +
  geom_point(data = iter_estocastico, colour ='red', alpha=0.5)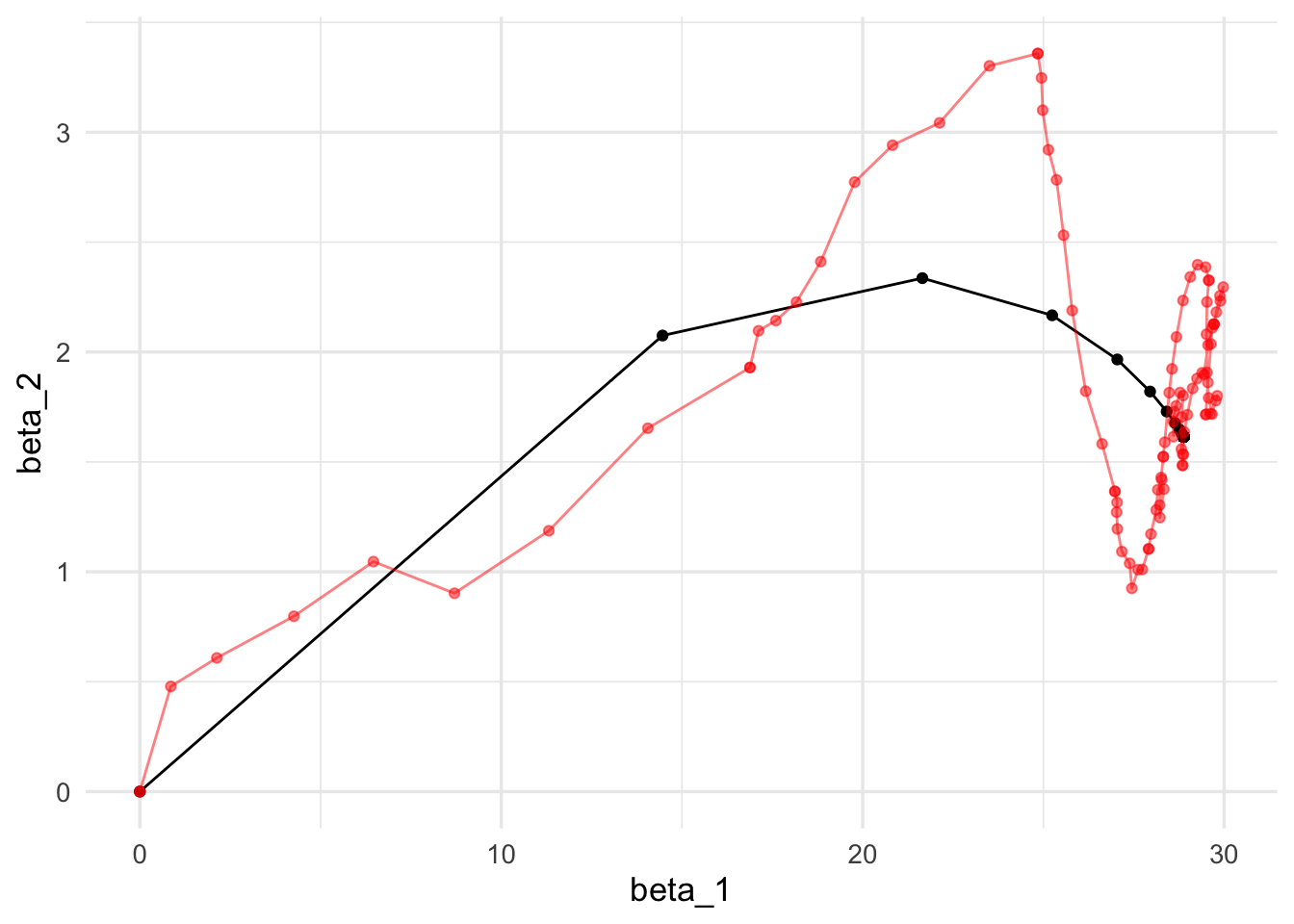

Nótese cómo llegamos más rápido a una buena solución (comparado con el ejemplo sin momento). Adicionalmente, error de entrenamiento y validación lucen más suaves, producto de promediar velocidades a lo largo de iteraciones.

Valores típicos para momento son 0,0.5,0.9 o 0.99.

Otras variaciones

Otras variaciones incluyen usar una tasa adaptativa de aprendizaje por cada parámetro (algoritmos adagrad, rmsprop, adam y adamax), o actualizaciones de momento un poco diferentes (Nesterov).

Los más comunes son descenso estocástico, descenso estocástico con momento (a veces con la modificación de Nesterov), rmsprop y adam (Capítulo 8 del Deep Learning Book, (Goodfellow-et-al-2016?)). Por ejemplo, muchas veces se recomienda usar adam para redes profundas, o gradiente estocástico con momento.

11.15 Ajuste de redes con descenso estocástico 

set.seed(21321)
x_ent <- as.matrix(dat_ent[,c('x_1','x_2','x_3')])
x_valid <-  as.matrix(dat_valid[,c('x_1','x_2','x_3')])
y_ent <- dat_ent$y
y_valid <- dat_valid$y

Empezamos con regresión logística (sin capas ocultas), que se escribe y ajusta como sigue:

modelo <- keras_model_sequential() 
modelo |>
  layer_dense(units = 1, 
              activation = 'linear',
              input_shape = c(3))
modelo |> compile(loss = 'mean_squared_error',
  optimizer = optimizer_sgd(learning_rate =0.01, momentum = 0, decay = 0))
history <- modelo |> 
  fit(x_ent, y_ent, 
      epochs = 100, batch_size = 64, 
      verbose = 0,
      validation_data = list(x_valid, y_valid))

Podemos ver el progreso del algoritmo por época

aprendizaje <- as.data.frame(history)
ggplot(aprendizaje, 
       aes(x=epoch, y=value, colour=data, group=data)) +
  facet_wrap(~metric, ncol = 1) + geom_line() + geom_point(size = 0.5)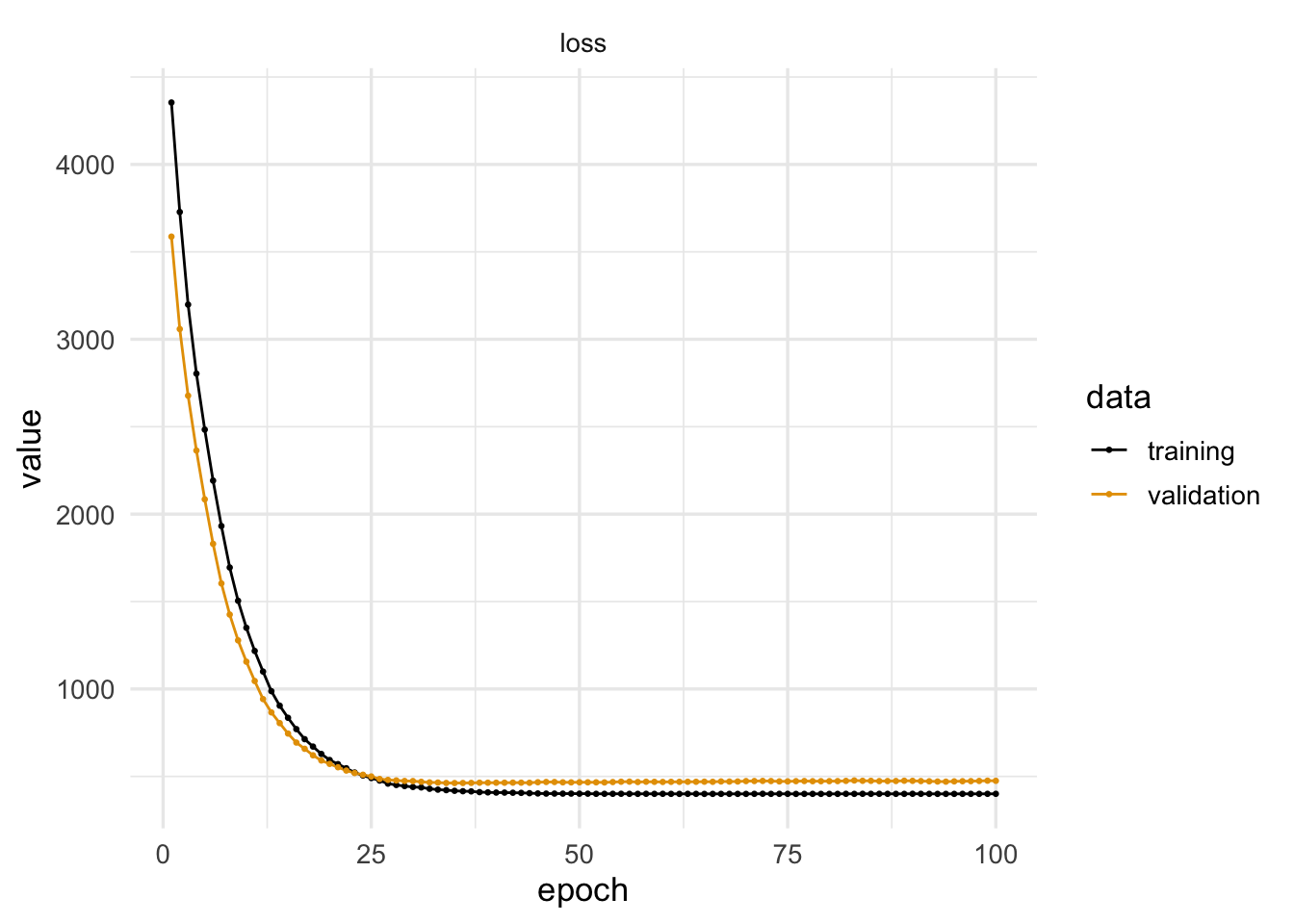

Ver los pesos:

get_weights(modelo)
## [[1]]
##           [,1]
## [1,] 28.948439
## [2,]  1.988662
## [3,] -3.667942
## 
## [[2]]
## [1] 56.80006

Y verificamos que concuerda con la salida de lm:

mod_logistico <- lm(y ~ x_1 + x_2+ x_3, data = dat_ent) 
coef(mod_logistico)
## (Intercept)         x_1         x_2         x_3 
##   56.527464   28.879848    1.613882   -3.358013